不均匀地基桥梁明挖基础变形分析

张永忠，关凤琚

(铁道第三勘察设计院集团有限公司，天津300142)

沉降变形是建(构)筑物安全可靠度分析的指标之一，随着科学技术的进步，对沉降变形检算的要求越来越高。明挖基础是铁路桥梁的常用基础形式之一，由于其施工工艺简单造价低而倍受青睐。近年来，对铁路基础结构沉降及桥梁明挖基础的研究已取得不少成果，涉及到的内容包括地基沉降对桥梁及基础结构的影响［1－4］，桥梁及基础沉降观测分析与预测［5，6］，基础设计程序的优化［7］、施工方法、处理措施等方面的研究［8］，对于不均匀地基明挖基础的沉降变形研究较少;目前已有的规范［9］对桥梁基础的沉降仅规定了单个墩台均匀沉降容许值，以及相邻墩台均匀沉降之差容许值，都没有涉及到单个墩台差异沉降方面规定。

在明挖基础勘察、设计、施工过程中，地基不均匀是常见问题之一。地基风化程度的不均匀，地基强度的不均匀将会造成基础的差异沉降，地基的不均匀范围、不均匀程度、不均匀深度是控制基础沉降及差异沉降的主要因素，现有规范较少给出该类问题的定量结果。

本文以工程实例为原型，概化出具有一般特性的基本模型，就地基不均匀深度方面进行计算分析，对在不同深度不均匀风化地基条件下桥梁明挖基础的沉降及水平变形进行数值计算，并借助matlab矩阵工具对沉降及水平位移曲线进行处理，得到沉降及水平位移与地基不均匀深度变化的函数关系式，为桥梁的勘察、设计、施工提供有益的帮助。

1 明挖基础变形计算及分析思路

以某铁路桥梁明挖基础为基本地质模型，在此基础上，为了研究具有一般意义条件下明挖基础在不同深度不均匀地基的情况下变形问题，将其抽象成更具一般特性的地质力学模型，进行数值计算，得到结果，具体步骤如下:

(1)依据实际工程基础结构形式与工程地质特征建立基本地质模型;

(2)依据基本地质模型进一步抽象为具有一般特征的地质力学模型;

(3)设置不均匀地基方案:基底左侧为弱风化玄武岩，基底右侧分为七层，从上至下强风化玄武岩深度依次加深，如表1所示;

(4)设置不同的计算工况，依据明挖基础左右两侧不均匀地基的深度设置不同的计算分析方案，如表1所示。

其中工况一基底左侧和右侧都为弱风化玄武岩，即均匀地基;工况八基底左侧为弱风化玄武岩，右侧为强风化玄武岩;其余工况为中间过渡工况;

(5)对八种工况进行计算分析，并运用matlab工具等对结果进行分析处理，得到不同深度不均匀地基条件下桥梁明挖基础沉降变形规律。

2 计算模型的建立

2.1 地质模型的概化

某高速铁路特大桥的一个明挖基础，基底地层风化不均匀，左侧为弱风化玄武岩(W2)，右侧0～5 m为强风化玄武岩(W3)，下部为弱风化玄武岩(W2)，如图1，2所示，但地基承载力均满足设计值要求，为了避免基础左右两侧发生差异沉降值太大，影响桥梁稳定性，需对其沉降及水平位移进行计算论证。

为了使得分析计算结果更具有一般性，本文在上述实例基础上，对工程地质条件进行了抽象概化，建立如图3所示的地质模型，即剖面基底弱风化基岩与强风化基岩界线为中心式分界模式。对强风化岩石地基的发育深度按照分析思路的工况分别进行讨论。本文共分八种工况，设定了八种不同深度的强风化岩石，在此条件下建立模型，进行数值计算分析。

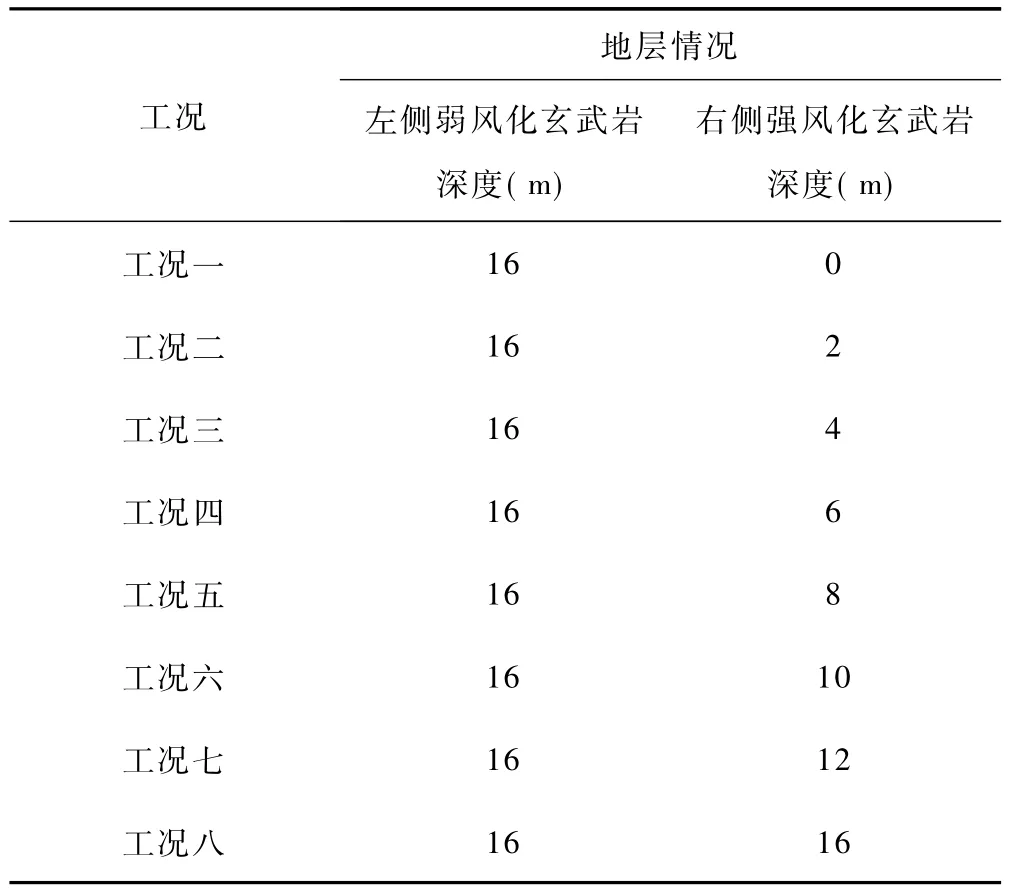
表1 不同深度不均匀地基明挖基础计算工况

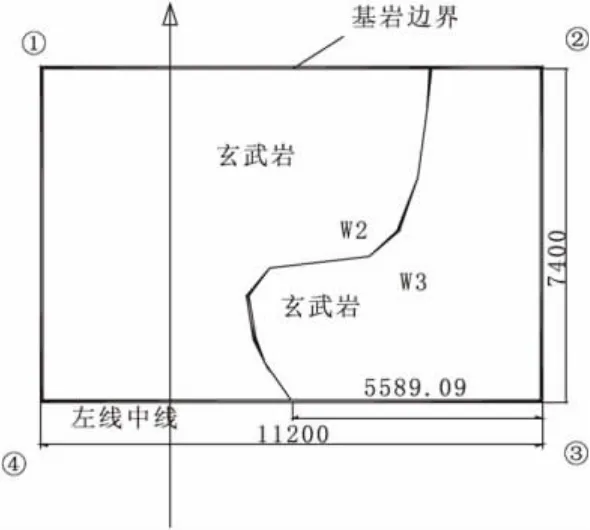
图1 明挖基础基坑平面图

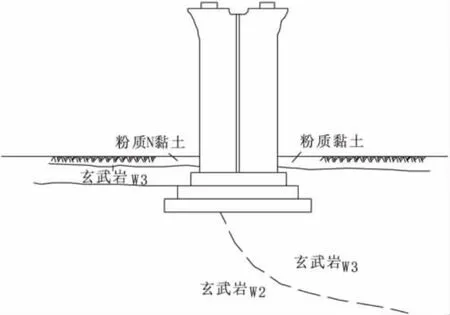
图2 明挖基础剖面图

2.2 力学模型的建立

力学模型主要依据地质模型特征建立，左右边界为水平位移约束，底边界为纵向与水平位移约束边界，桥墩顶部为力学边界，分别承受上部纵向荷载与水平荷载;本次计算按照时速250 km设计标准［9］，主应力+横向附加应力荷载组合进行计算，水平荷载500 kN，竖向荷载20 000 kN，桥墩两支座中心间距4.5 m，具体模型如图3所示。

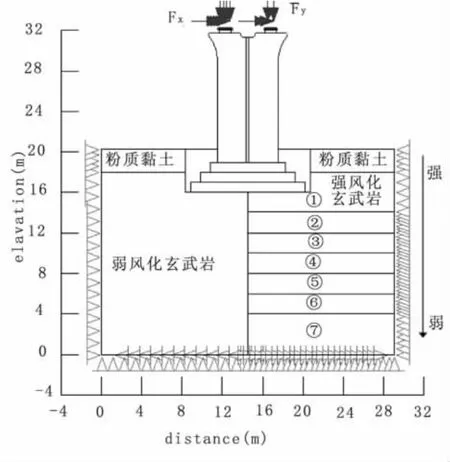
图3 明挖基础地质力学模型

2.3 物理力学参数的选取

物理力学参数主要参考岩石力学参数手册［10］，并结合工程试验结果选取，具体数值如表2所示。

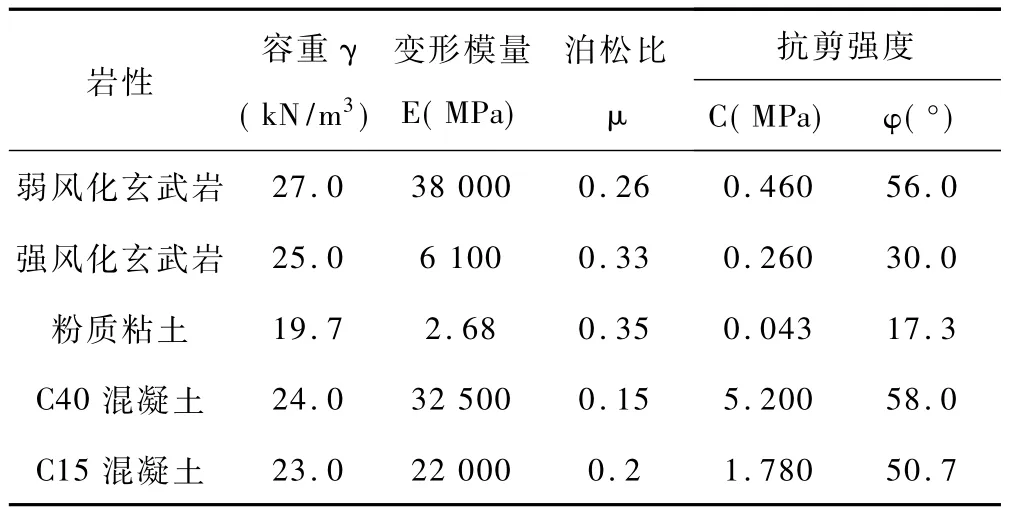
表2 地基与基础的物理力学参数表

3 计算结果分析

3.1 沉降分析

图4为明挖基础沉降云图，从图中结果可知:

(1)在不均匀地基条件下的明挖基础会发生差异沉降，地基强度低(强风化玄武岩)的一侧沉降量大于强度高(弱风化玄武岩)的一侧;

(2)基础顶部沉降量最大，向下直到地基依次减小;

(3)桥墩左右支座差异沉降最为显著，向下直到地基依次减小，地基下部差异沉降逐渐接近于零。

表3为明挖基础位移统计表，表4为明挖基础位移函数表，图5、6为明挖基础支座沉降曲线，从表中结果分析可知:

(1)随着地基强度较低(强风化玄武岩)地层深度的增加，桥墩支座的沉降量逐渐增大，增幅逐渐减小;

(2)桥梁基础差异沉降量随着地基不均匀深度的增加逐渐增加，但增幅逐渐减小;在工况八条件下，左右支座的差异沉降达到2.42 mm;

(3)通过表4可以得到左右支座沉降及差异沉降曲线都呈对数形式增长，增长速度逐渐减缓;

(4)依据桥梁设计规范，该条件下桥墩沉降量在容许范围内，但对桥梁位移控制有一定影响，且随着不均匀深度的增加，位移量呈增长趋势。

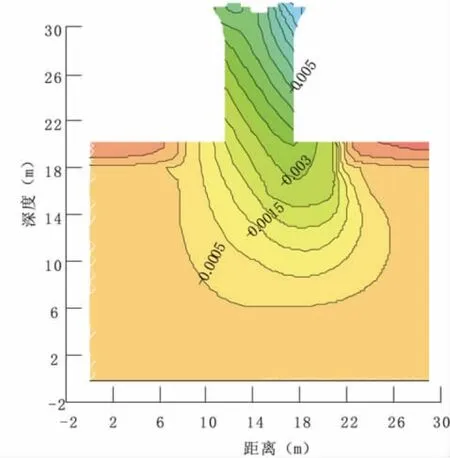
图4 明挖基础沉降云图

表3 明挖基础位移统计表

3.2 水平位移分析

图7为明挖基础水平位移云图，图8、9为扩大基础水平位移曲线，从表3、4及图7、8、9结果分析可知:

(1)基础水平位移左右两侧差值较小，位移等值线较为平缓;

(2)基础顶部水平位移及水平位移差值最大，向下直到地基逐渐减小;

(3)左右支座水平位移随地基不均匀深度的增加不断增加，位移曲线呈对数形式增长，增长幅度逐渐变缓;

(4)左右支座水平位移差值为常数，即其值不随地基不均匀深度的增加而变化，曲线为水平直线。

表4 明挖基础支座位移函数表

图5 明挖基础左右支座沉降曲线

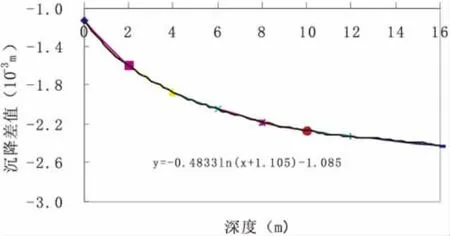
图6 明挖基础左右支座差异沉降曲线

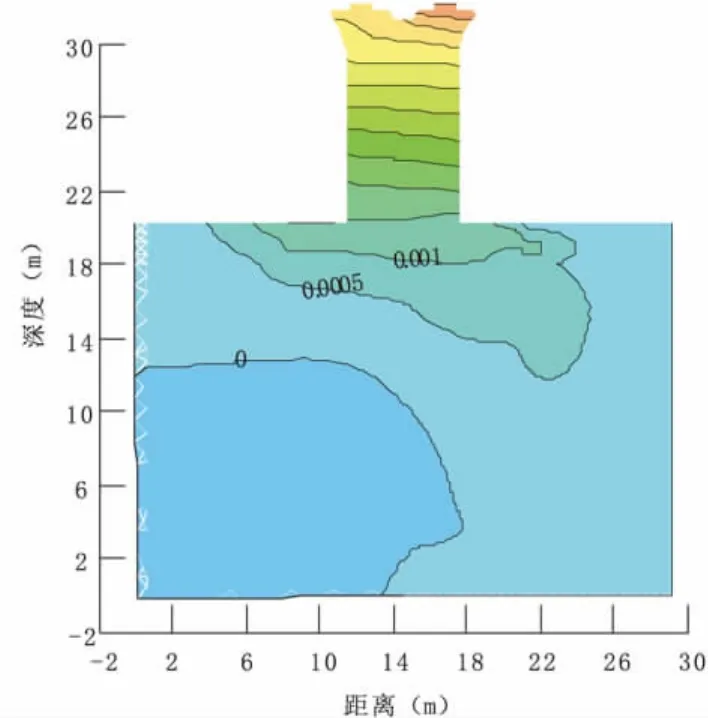
图7 明挖基础水平位移云图

3.3 应力分析

图10为明挖基础最大有效应力云图，从图中结果分析可知:

(1)桥墩支座应力最大，应力集中程度最高;

(2)基底部分地基强度越高(弱风化玄武岩)应力越大，强度较低一侧(强风化玄武岩)应力水平较低;

(3)玄武岩弱风化与强风化界面处应力较集中，为易破坏区;

(4)靠近强风化玄武岩一侧的桥墩应力较另一侧大，向下直到地基应力值减小速度较快。

通过上述应力结果分析可以得到:桥梁上部荷载通过桥墩向下传递到地基，地基部分主要由强度较高一侧的地层岩土体来承担荷载;桥墩部分靠近地基强度较低一侧的压应力偏高，可能形成薄弱区域。

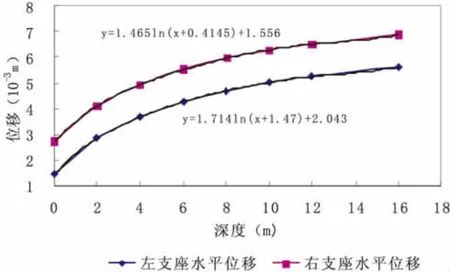
图8 明挖基础水平位移曲线

图9 明挖基础差异水平位移曲线

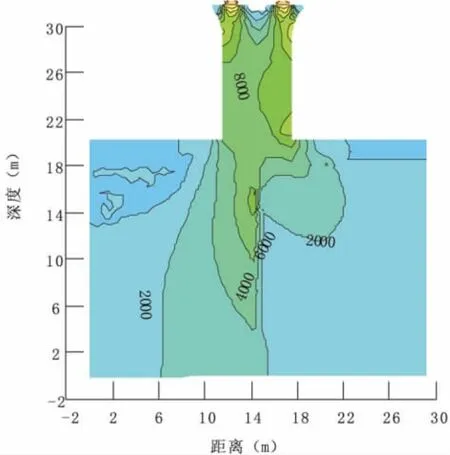
图10 明挖基础最大有效应力云图

4 结论

本文主要结论有:

(1)不均匀地基明挖基础会发生差异沉降及水平位移差，地基强度低的一侧基础沉降量及水平位移量较大;

(2)不均匀地基明挖基础变形函数如表4所示，其中沉降量函数、差异沉降量函数、水平位移量函数为对数函形式，水平位移差函数为常数;

(3)基础顶部位置沉降量、差异沉降量、水平位移量、水平位移差值最大，向下直到地基逐渐减小;

(4)随着地基不均匀深度的增加，基础沉降量、差异沉降量、水平位移量呈对数函数形式增长，但增幅逐渐减小;

(5)水平位移差值不随地基不均匀深度的变化而变化，其值为常数;

(6)基础基底部分地基强度越高应力水平越高;

(7)地基中软硬分界面应力集中，易成破坏区。

上述结论表明:当地基不均匀时，桥梁明挖基础的沉降量、水平位移量、差异沉降量随着不均匀深度的增加呈增长趋势，其函数呈对数函数形式，增长趋势逐渐减小;地基中强度较高岩土体及靠近地基强度较低一侧的基础部分为偏压区域，应从变形角度分析基础的适应性，并验算其安全可靠度。

［1］李国和，孙树礼，许再良，张建民.地面沉降对高速铁路桥梁工程的影响及对策［J］.铁道工程学报.2008(4):37－41，61.

［2］黄纳新.连续刚架桩基础的不均匀沉降特性分析［J］.铁道勘测与设计.2002(3):18－21.

［3］宋国华，高芒芒，黎国清.桥梁墩台不均匀沉降时的车桥垂向系统耦合振动分析［J］.中国铁道科学.2010(2):29－33.

［4］李隆平.地基基础弹性变形对明挖基础桥墩设计的影响［J］.科学技术通讯.1999(1):9－13.

［5］杨吉新，李佳明.哈大客运专线桥涵基础沉降观测分析与建议［J］.铁道工程学报.2010，136(1):38－41.

［6］杨吉新，朱伟伟，丁兰.哈大客运专线桥梁墩台沉降观测与预测［J］.铁道工程学报.2010，142(7):42－46.

［7］李志明，王丽娟，王扬.明挖扩大基础的设计与计算［J］.交通标准化.2006，158(10):62－63.

［8］刘英姿.扩大基础挖基问题及处理措施［J］.西部探矿工程.2004(2):15－16.

［9］铁路桥涵地基和基础设计规范［S］.北京，2005:2005.

［10］水利水电科学研究院等.岩石力学参数手册［M］.北京:水利水电出版社.1991.