不同尺度遥感影像上水体提取效果分析

杨旭艳，赵 婷，2

(1.西北大学 城市与环境学院，陕西 西安710127;2.丹凤县气象局，陕西 丹凤726200)

尺度概念是理解地球系统复杂性的关键，地表信息在时间上和空间上的分辨率都有极大的跨度在某一个尺度上人们观察到的性质、总结出的原理规律，在另一尺度上可能仍然是有效的或是相似的，但也可能需要修正，因为在一个空间尺度上是同质的现象到另一个空间尺度就可能是异质的，从而地理实体或现象的空间分布模式往往呈现出一定的尺度依赖性。基于尺度的空间问题的研究才能真正揭示各类地理对象或现象空间分布的客观规律。

尺度效应问题是不同分辨率遥感图像之间的关系、不同的自然现象有不同的最佳观测距离和尺度，需要适当的距离和比例尺，才能有效完整的观察，并不是距离越近越好，观测越细越好，因为只有在一定的尺度范围内特定地物的特征才能尽可能完美的呈现出来但距离越远混合像元越多，对研究对象的刻画越来越模糊，无法描述应有的细节[1]。本文提取水系的适宜尺度，做了定性的分析。

1 数据和方法

研究使用的遥感数据为陕西省西安市SOPT5多光谱影像，数据获取时间是2008年7月，经过对图像的几何精校正、图像增强、波段选择等预处理后，从中截取大小为4228×3647的图像作为研究区(如图1)。

图1 原始试验区10m

本次研究分为四个主要部分:

(1)对原始图像进行预处理:几何校正，并且添加投影信息，裁切4228×3647图像作为实验区;

(2)对源图像进行尺度转换，并进行结果评价，选择出最佳尺度转换方法;

(3)在不同的尺度下提取水系，并分析在不同尺度上水系不同的变化。

2 尺度转换实验

2.1 尺度转换方法

遥感图像尺度转换的方法按转换图像的波段数分为两大类:①基于像元的尺度转换方法，基于像元的数理统计方法主要依靠的是源数据像元的灰度值，将其作为尺度转换的依据和基础数据，数理统计的方法都是用于尺度上推，可以将高空间分辨率遥感图像转换为低空间分辨率图像[2]。②融合的转换方法，根据融合转换也是一种基于统计的多波段图像尺度转换的方法，适用于尺度下推，通过将高空间分辨率图像上的部分信息融入到低空间分辨率的图像上，从而达到提高低空间分辨率图像的分辨率。在尺度转换的过程中，基本的原则是在尽可能的保持原始图像光谱信息的前提下，提高图像的空间分辨率。

本文是基于一系列的尺度上推实验，采用基于像元的尺度转换方法，下面是几种基于像元数理统计的尺度转换方:

2.1.1 局部平均法

局部平均法是将高空间分辨率遥感图像转为低空间分辨率图像的一种基本方法，设置一定大小的窗口，将窗口内的所有像元值的均值作为相应尺度转换后的低分辨率遥感图像的像元值，然后将窗口滑动，依次计算下一个尺度转换后图像中的像元值。

2.1.2 中值采样法

中值采样法就是在遥感图像上开一定大小的窗口，将窗口内所有像元值的中位数值作为相应的尺度转换后的低分辨率遥感图像的像元值，然后将窗口滑动，依次计算下一个尺度转换后图像的像元值。

2.1.3 最邻近法

最邻近法，就是将原始遥感图像中离尺度转换后对应像元最近的像元值赋给转换后对应的低分辨率遥感图像像元，依次计算每个尺度转换的像元即完成了尺度转换。

2.1.4 双线性内插法

双线性内插也被称为一次内插法，算法的基本原理是:将原图像中两个正交方向上(即四邻域方向内)的像元值按照距离加权的方法进行内插，将所得值赋予尺度转换后对应位置的低分辨率图像的像元。

2.1.5 立方卷积法

也称为三次卷积法，立方体卷积内插法的原理同双线性内插的原理，其区别是立方体卷积法中是用原图像中某像元及其周围16个像元的加权平均值作为转换后遥感图像对应位置的像元值。

2.2 尺度转换实验

本次实验的基础数据是SOPT510m的遥感图像，以此数据为基础，进行尺度上推转换，得到一系列大尺度低分辨率的图像，为了体现水系在不同分辨率图像上的不同形态和形状。本文选用五种尺度转换的方法:局部平均法、中值采样法、最邻近法、双线性内插法、立方卷积法。用五种方法得到的五组系列尺度的图像将通过尺度转换效应分析，选择尺度转换后保持源图像各项指标效果最好的一组数据作为后续地物特征提取工作的基础数据。

局部平均法和中值采样法是在软件ErdasImage9.2中通过建模完成的，在图像上开3×3窗口，分别用平均值法和中值法对源图像进行计算，设置输出图像栅格的大小(即输出图像的尺度)，最终得到尺度转换结果图。

最邻近法、双线性内插法和立方卷积法都是在ArcGis9.3软件的toolbox中Raster模块下的resample工具下实现的，由中心像元及其邻域的像元值分别计算最邻近值、双线性内插值和三次卷积值作为新图像该位置的像元值，设置输出栅格的尺寸，就得到尺度转换结果图。

2.3 尺度转换评价指标

遥感图像在进行尺度转换后，会不可避免地导致图像有不同程度的信息损失或变异，并且利用不同方法进行尺度转换，光谱信息和特征信息的损失程度也会不一样[3]。目前，还没有一个明确的方法或者指标专门用来评价尺度转换结果的好坏，只能根据一些与遥感图像质量密切相关的系数或者指标从不同的方面反映尺度转换前后图像的质量，通过比较不同转换方法得到的图像与原始图像的在某些方面的接近程度，都可以作为衡量图像尺度转换方法的指标。

信息容量(iformation capacity)是计算机图形图像学领域的一个概念，是像素密度的信息承载能力的数量单位。信息容量的优点:①度量方法上，信息容量是一种基于多维直方图的灰度数字图像质量评价统计模型，计算时考虑了像元之间的相关关系，较信息墒(只对鼓励像元统计)更能客观的反应地物的结构及电磁辐射特性;②信息容量对图像评价结果和人类的视觉评价结果相一致，具有人类视觉响应的特点，克服了传统评价方法中与人的视觉评价结果不一致的问题。

每一幅灰度图像都可以做出一维直方图，通常可以用它来大致判断图像质量的好坏。数字图像的重要特征是像素灰度值的随机分布，直方图是图像的一种宏观统计。直方图能大概的描述图像的灰度范围，灰度的分布和每个灰度级的频数，以及整幅图像的对比度和平均明暗程度，这对图像的处理和分析具有重要作用[4]。一维直方图虽然能提供图像特性的许多信息，但它只是对孤立像元的统计，不能统计图像像素间的相关关系。所以，根据数字图像的一维直方图只能得到图像的一些基本信息。为了统计像素间的相关关系，就要用到高维直方图，对于一幅数字图像g(x，y)，设其行列值分别是m 和 n，其频数表示为{Num(G1，G2，…，Gk)|(G1，G2，…，Gk∈O)}，即表示满足该图像中某一像素灰度值为G1，而和该像素相关的(k－1)个像素的值为G2，…，Gk时的像素集的个数，称频数的集合{Num(G1，G2，…，Gk)|(G1，G2，…，Gk∈O)}为 k 维直方图。

二维直方图可以描述相邻像素之间的相关性质，同时有利于分析图像的宏观统计特性，又比较容易计算，并且和更高维的直方图没有本质的区别，所以定义二维直方图{Num(G1，G2)}为某像素灰度为G1，而其相邻邻像素点灰度为G2的像素频数。假设某一像素的灰度为x1，而其右边相邻像素的灰度值为x2，根据二维直方图的性质则有:如果二维直方图的值集中在对角线附近，就说明图像的质量比较好，如果二维直方图的值较为分散，没有明显的集中趋势，则说明图像的质量较差。通过图像直方图的特性和分形维数的原理可得出，图像二维直方图的灰度层次可根据分形维数的思想来评价，即用相同的维数去量度一个确定的几何体，得到的结果就是一个确定的维数，对于图像的二维直方图来说，这个维数可描述图像的灰度级的丰富程度。

可以用最大频数值max{Num(G1，G2)}对二维直方图进行归一化，得到二维峰值归一化直方图，即{Norm(G1，G2)}，

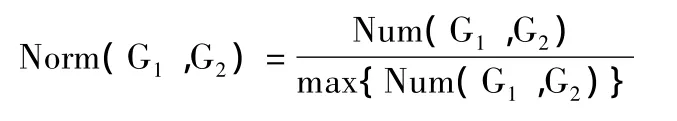
如果用频数峰值的对数将其归一化，得到的集合{Norm－LOG(G1，G2)}则称为二维对数峰值归一化直方图，其中

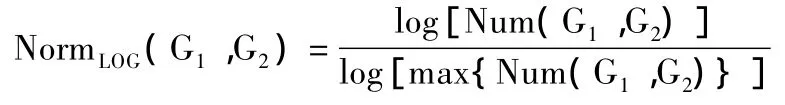
二维直方图频数的峰值归一化直方图和频数的对数峰值归一化直方图的值都在0～1内，从分形维数的复杂性量度思想上考虑，用直方图的最大值对频数进行归一化，能够将直方图的细节变化表现出来。二维对数峰值归一化直方图中，峰值变化对图像中其它灰度值的影响减小。从分形的观点来看，对数峰值归一化直方图反映了遥感灰度图像中灰度级的丰富程度及其分布的复杂性。在二维对数峰值归一化直方图的基础上，引入信息容量的概念。对数峰值归一化直方图在约束区域ω⊆Ω上的累积对数变换，就称为信息容量[4]，可表示为:

本文采用信息容量(Cinfo)来评价尺度转换的结果，在Matlab下编写程序计算各个尺度上的信息容量，下表1是不同转换方法得到的不同尺度遥感影像的信息容量。

为了比较清楚反应各种转换方法得到的结果和源图像的信息容量的差异，将表中的数据用折线图表示，见图2。

从上面的折线图上可以看出，这三种方法计算得到的信息容量的值是随着尺度的增大而减小的，最邻近法和双线性内插方法得到的结果变化趋势不规则，而三次卷积法得到的结果是近似呈现出一条直线的，符合信息容量与尺度之间的变化关系，即随空栅格尺寸的增加而逐渐变小。因此选择三次卷积法得到的图像和源图像作为本次实验研究的基础数据。下面是用三次卷积法得到的系列尺度图3。

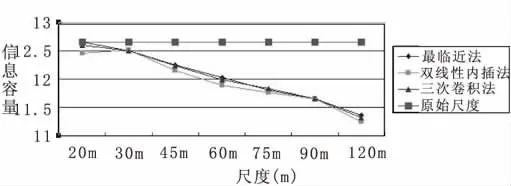
图2 信息容量评价指标图

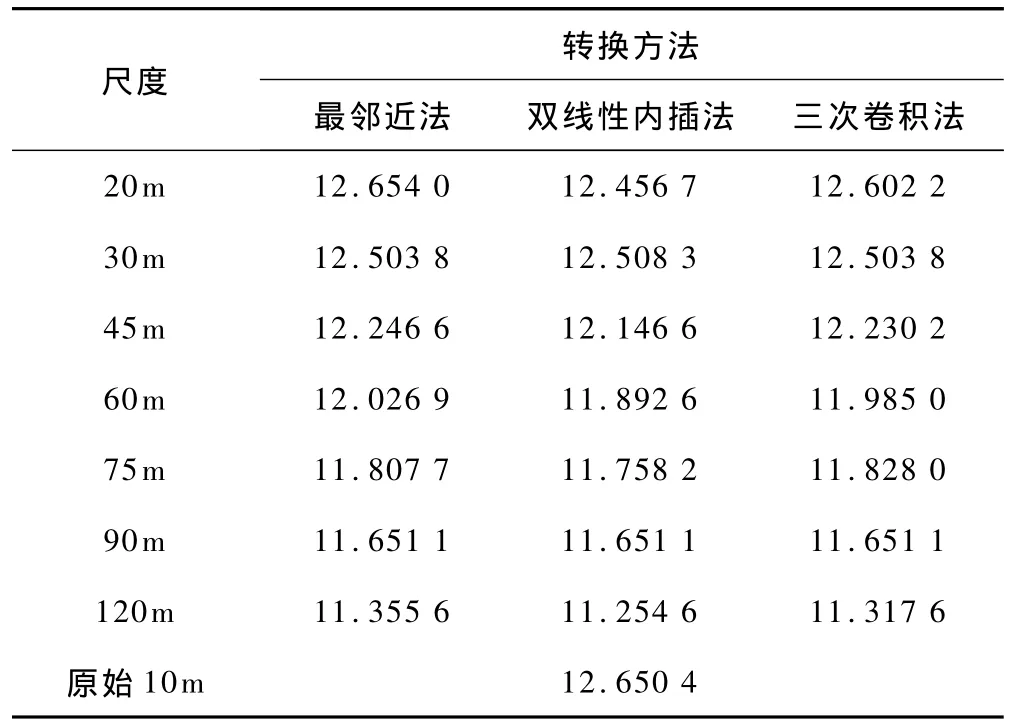
表1 信息容量法尺度效应评价指数值

图3 三次卷积法尺度转换系列影像

3 水体提取实验

在以上实验的基础上分别在原始10m，以及转换后的20m，30m，45m，60m，75m，90m，120m 的遥感影像上提取水系样本。

3.1 归一化水体指数模型计算

在 ERDAS IMGINE 9.2下建模计算(Modeler模块)，分以下几步:

(1)进行源影像裁剪，得到研究区域的band1(绿色)和band4(短波红外)波段的遥感影像文件;用Modeler模块的function函数集计算 band1－band5和 band1+band5，并将结果暂存;

(2)用Eeiher if函数判断每个像素的除数band1+band5是否为零，若为零则赋值－1，若不为零，则赋值为(band1－band5)/(band1+band5)，并将结果保存在临时存储器中;

(3)使用(DN－min)*255/(max－min)函数计算每一个像素的NDWI值。

最终可以得到研究区域的NDWI图像，其取值区间从0－255，与SPOT原始数据有同样的灰度级。

3.2 图像的二值分割

所得研究区的 NDWI值图像只是一个灰度图，若要提取水域，仍需要做灰度分割，此处的灰度分割算法实质是图像的二值化。首先用不同选区的感兴趣区AOI(Area of interest)，对 NDWI图像进行裁剪，统计各个水域的平均值，根据多次实验，最终确定图像分割的阈值为135，按该阈值二值化后的水域提取效果图[6]。NDWI法可以准确的将较宽的水体准确的提取出来，没有多提取的现象单波段阈值法无法提取的影像上部水域也可以准确提取，但对较小的水体提取仍然有一些局限性[7]。

3.3 不同尺度遥感影像上提取得到的水系

从不同尺度遥感影像上提取得到的水系见图4。

图4 不同尺度影像上水系样本

由图4可以看出，随着尺度的增大，图像栅格尺寸也增大，地物样本的形状边界逐渐模糊化，样本的边界不再是圆滑的，越加显得阶梯化，样本的边界钝化。并且在水系提取的过程中，尺寸越大，提取水系的难度也越来越大，到了120m的时候就很难再提出完整的水系了。

进一步分析上面的水系，在10m，20m，30m和45m分辨率上提取的水系，基本上是比较完整的，边界清晰，跟实际的情况符合度比较高，因此，在这种定性分析的基础上，可以认为水系在10m到45m的尺度上提取会有比较好的效果。

4 结语

本文采用三种经典方法对源图像进行尺度转换，得到了三组系列尺度的图像数据，源图像的信息在传递到不同尺度的图像过程中不免会发生不同程度的损失和转移，利用尺度效应指标(信息容量)可以反映出尺度转换后的图像与源图像在某些图像评价方面的接近程度。分析尺度效应评价指标计算结果可以得出:经过尺度转换后的图像中，运用三次卷积法转换得到的图像较其他方法能够较好的保持源图像的光谱性能、清晰度和信息量等，故作为典型地物特征提取的基础数据。

在三次卷积法转换后的系列尺度图像上运用归一化水体指数提取水体，分析其再不同尺度上的差异性，结果表明:在10m分辨率到45m分辨率之间提取的水系比较完整，边界清晰，而随着分辨率的不断增加，到120时就很难提取水系的大致形状。从得到的不同尺度上提取的水系经过与实际情况的对比，以及目视解译分析结果只是一个定性的分析，没有达到定量的要求，因此如何用一个定量的评价指标来选择水系提取的最佳尺度，以及应用于实践中，是以后工作和研究的重点。

[1]杨邦，任立良，王贵作，刘晓帆，李国芳.基于尺度转换的数字水系提取方法及应用[J].中山大学学报(自然科学版).2009，28(4):103－112.

[2]SU Fenzhen，GAO Yi，ZHOU Chenghu，YANG Xiaomei，FEI Xianyun.Scale effects of the continental coastline of China[J].Journal of Geographical Sciences.2011.21(6):1101－1111.

[3]韩鹏，龚健雅，李志林，程亮.遥感影像空间尺度上推方法的评价[J].遥感学报.1007－4619(2008)06－0964－08.

[4]屈颖歌，曾生根，夏德深.从图像信息容量和图像功率CBERS－1卫星图像[J].航天返回与遥感.2002，23(2):40－45.

[5]姜宁宁，庞莎.基于 GIS的延安市城郊区土地生态重要性分析[J].地下水.2011，33(1):152 －153.

[6]周德民，程进强，熊立华.基于DEM的洪泛平原湿地数字水系提取研究[J].地理科学.2009，20(3):118－121.

[7]刘金涛，张佳宝，刘建立，李晓鹏.融合多源数字信息的流域水系提取方法研究[J].地理与地理信息科学.2010，26(2):27－30.

[8]YU lei，LIU hongbin，WU wei.Extraction of River Networks in the Three GorgesArea in Chongqing Based on DEM[J].地理科学.2006，26(5):616－620.