冲击波感度临界隔板厚度的优化试验方法

王典朋，田玉斌，刘柳

(1.北京理工大学 理学院，北京100081;2.中国工程物理研究院 化工材料研究所，四川 绵阳621900)

0 引言

在测定主炸药冲击波起爆感度的方法中，隔板试验是经典试验之一。该方法主要通过增减衰减板厚度，调节输入的冲击波压力，最终估计炸药以50%概率发生爆轰的衰减板厚度［1-2］(简称临界隔板厚度)。临界隔板厚度是表征弹药主装药的冲击起爆感度，决定其安全性和可靠性的一项重要参数。

目前，我国主要应用升降法［3］进行隔板试验［1，4］:1)假设主装药的感度分布为正态分布，具有形式Φ((x-μ)/σ)，μ 是主装药以50%概率发生爆轰的隔板厚度，σ 表示感度分布的标准差;2)根据经验确定初始隔板厚度x1和试验步长d;3)根据第i次试验的结果yi(yi=0 表示未发生爆轰，yi=1 表示发生爆轰)，按如下方式调整隔板厚度(也称为试验水平)

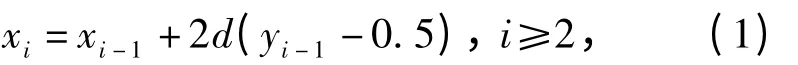
即第i 次试验若发生爆轰，增加隔板厚度d 个单位(否则，减少隔板厚度d 个单位)，得到下一次试验的隔板厚度;4)在获得样本量为n 的试验数据(x1，y1)…，(xn，yn)后，应用似然方法求出两个参数μ，σ 的极大似然估计。此时，在数学理论上有一限制条件［5］，即只有试验数据存在交错区间(即发生爆轰的最大隔板厚度小于不发生爆轰的最小隔板厚度)，两个参数的极大似然估计才存在唯一解。否则按照试验数据无法求出μ，σ 的极大似然估计(这样的试验数据称为无效试验数据，相应的升降法试验称为无效试验)。

应用升降法试验估计主装药的临界隔板厚度简单易行，但是有如下缺点:1)升降法试验不具有数学上的优化特性，在相同的样本量下估计精度有待进一步提高，或者在相同的估计精度下样本量有待进一步减少;2)在升降法试验开始时，需要猜测试验步长d.如果步长猜测的较大，产生无效试验数据的机率增大，从而增加了试验的不确定性。

Neyer 方法也可以用来估计临界隔板厚度。Neyer 方法的试验策略分3 个部分:1)猜测μ 的取值范围［μmin，μmax］和σ 的值σg，探索试验水平的范围;2)快速寻找交错区间，使得参数的极大似然估计唯一存在;3)通过最大化数据对应的Fisher 信息矩阵

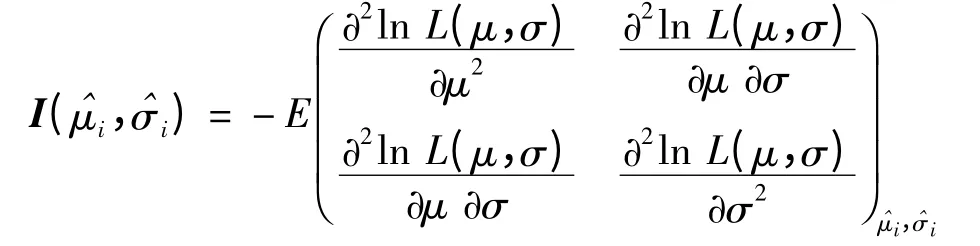
的行列式来选择第i+1 次试验水平，其中L 为数据对应的似然函数，是利用前i 组数据计算的(μ，σ)的极大似然估计。具体步骤参见文献［6］.Neyer 方法同样存在无效试验的情况。在σg猜测较大的时候，产生无效试验的几率也急剧增加，但是较升降法已经有了很大的提升。下面以感度分布Φ((x-μ)/σ)，μ=10，σ=1 为例，在各种可能的初始猜测下，以获得1 000 次有效试验数据为目的，模拟了样本量为10 和20 的升降法和Neyer 方法试验。表1～表4展示了伴随发生的无效试验的次数和比率。在模拟中，升降法的初始试验水平为μ 的猜测值μg，步长d = σg;Neyer 方法的初始猜测为μmin=μg-4σg，μmax=μg+4σg以及σg.

表1 样本量为10 时的无效升降法试验次数和比率Tab.1 The count and rate of the Up-and-Down’s unavailable data when the sample size is 10

表2 样本量为10 时的无效Neyer 方法试验次数和比率Tab.2 The count and rate of the Neyer’s unavailable data when the sample size is 10

表3 样本量为20 时的无效升降法试验次数和比率Tab.3 The count and rate of the Up-and-Down’s unavailable data when the sample size is 20

表4 样本量为20 时的无效Neyer 方法试验次数和比率Tab.4 The count and rate of the Neyer’s unavailable data when the sample size is 20

表1～表4展示的模拟结果表明，升降法在试验步长较大时出现大量的无效试验，Neyer 方法在σ猜测较大时无效试验的次数也急剧增加。为了避免无效试验，本文基于优化随机逼近思想提出了一种新的试验方法(称为优化随机逼近方法)。新的方法不需要用极大似然方法进行参数估计，因此有效避免了无效试验，克服了升降法和Neyer 方法的缺陷。

1 优化随机逼近方法

1.1 数学模型

将升降法扩展至更一般的试验设计形式，按照以下公式调整隔板厚度，

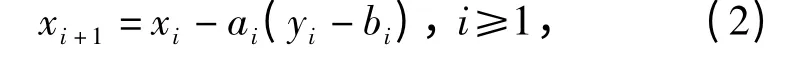
式中:xi为第i 次试验的隔板厚度;yi为相应的试验结果;{ai}和{bi}为常数序列。在升降法试验中，ai= -2d，bi=0.5.令Zi=xi-μ，则模型(2)式可以转化为

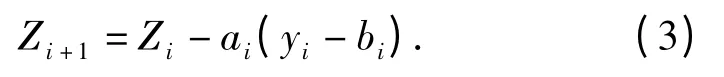
应用Bayesian 思想，根据历史数据或经验选择参数μ 的先验分布。选择初始试验水平x1为参数μ 的先验分布的均值，先验分布的方差τ21表明了用x1估计参数μ 的不确定性，则E(Z1)=0，D(Z1)=τ21.假设临界隔板厚度μ～N(x1，τ21)，此时若以90%的概率认为μ 在x1±5 区间内，则取τ1=3.039 8.

工程应用中，隔板厚度越大爆轰越不易发生。因此，在给定隔板厚度xi和参数μ，σ 时，

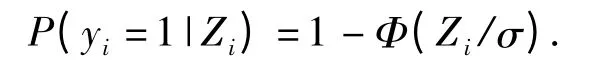
即给定隔板厚度xi和参数μ、σ，第i 次试验的结果yi服从二项分布

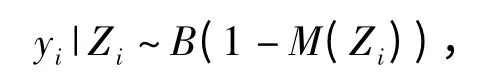
式中M(Z)=Φ(Z/σ).

在模型(3)式中，常数序列{ai}和{bi}满足一定条件时［7］，Zn以概率1 收敛到0.优化随机逼近方法选择{ai}和{bi}的依据为，使得E(Zi)=0，且达到最小。即在每一次试验中，隔板厚度都围绕μ 设置，而且设置的隔板厚度与真实临界隔板厚度之差具有最小的不确定性。

1.2 优化随机逼近中的常数序列

定理1 在优化随机逼近(3)式中，使得E(Zn+1)=0，且D(Zn+1)= τ2n+1达到最小的an和bn具有如下形式:

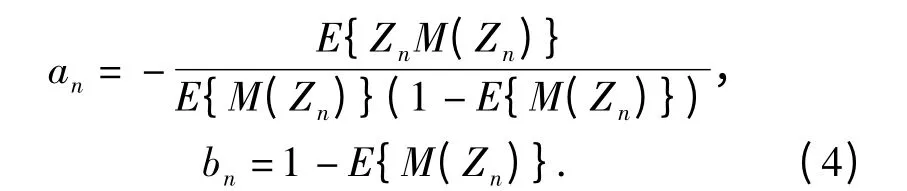
证明 由迭代公式(3)式，可以得到

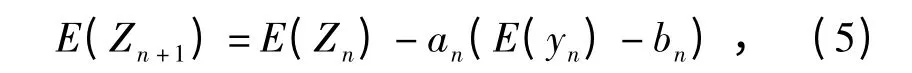
将E(yn)=E(E(yn|Zn))=1 -E{M(Zn)}代入(5)式，令(5)式等于0，则E(Zn+1)=E(Zn)-an(1 -E{M(Zn)}-bn)=0.

由于在迭代过程中E(Z1)=0，…，E(Zn)=0，所以有bn=1 -E{M(Zn)}.

由于E(Zn+1)=0，则D(Zn+1)=E(Z2n+1)，

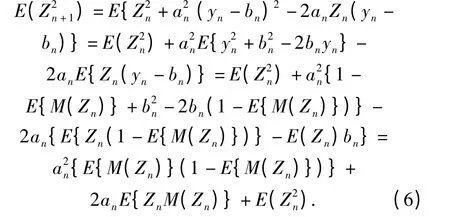
最小化(6)式，可以得到

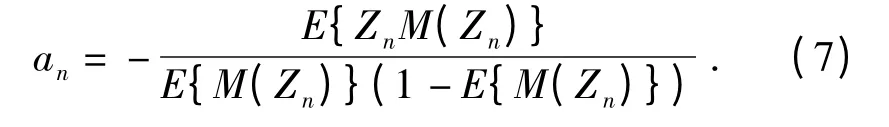
(7)式没有具体的解析形式，难以进行实际应用。文中用具有相同二阶矩的正态分布近似Zn的分布，得到以下{an}和{bn}的近似迭代公式。

定理2 假设Zn的近似分布为N(0，τ2n)，即E(Zn)=0，D(Zn)=τ2n，n≥1.令β =1/σ，则有

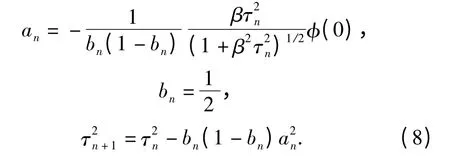
证明 由定理1 的结论和Zn的近似分布为N(0，τ2n)，n≥1，有将an和bn带入到(6)式即可得到的迭代公式。

由(8)式和包含升降法的一般试验设计形式(2)式可以进一步看出，升降法不具有最优性。根据文献［7］，在常数序列(8)式条件下，Zi依概率收敛于0，并且收敛性与初始猜测x1和τ1无关。根据该性质，完成样本量为n 的试验后，用(2)式得到的第n +1 次试验水平xn+1来估计临界隔板厚度μ.

本文方法与升降法和Neyer 方法最主要的区别在于以下3 点:优化思想不同，试验设计方法不同，数据分析方法不同。1)升降法虽然具有(2)式的形式，但不具有优化思想;Neyer 方法将试验水平尽可能散布在感度分布的0.2 和0.8 分位数附近来最大化数据对应的Fisher 信息矩阵的行列式;本文方法是通过使E(Zi)=0，且D(Zi)=τ2i达到最小将试验水平设置在临界隔板厚度附近，并且围绕临界隔板厚度变化的稳定性达到最好。2)升降法选择ai=-2d，bi=0.5 均为固定的常数，利用(2)式选择下一个试验水平;Neyer 方法在获得交错区间之后，通过最大化Fisher 信息矩阵的行列式来确定下一个试验水平;本文方法通过使E(Zi)=0，且D(Zi)=τ2i达到最小来优化选择{ai}和{bi}，然后利用(2)式选择下一个试验水平。3)升降法和Neyer 方法均需要利用数据(x1，y1)…(xn，yn)，建立似然函数L，并求解参数μ 和σ 的极大似然估计，然后用μ 的极大似然估计来估计临界隔板厚度;本文方法是按照Bayesian 方法用第n +1 次试验水平xn+1来估计临界隔板厚度。

由于上述不同，本文方法与升降法和Neyer 方法的数据分析结果也将存在差异。下一节将通过蒙特卡洛模拟方法来研究新方法与升降法和Neyer 方法估计临界隔板厚度的差异。

2 模拟研究

下面用蒙特卡洛方法将本文所提方法和升降法、Neyer 方法进行模拟比较。假设主装药的冲击波感度分布为正态分布N(x|μ，σ2)，μ =10，σ =1［8］.在各种不同的初始猜测下，应用本文方法、升降法和Neyer 方法估计临界隔板厚度。在模拟中，给定μ，σ 的猜测值μg和σg，按照国军标GJB/Z377A—94 的建议，在升降法中取x1=μg，d =σg;在Neyer 方法中，取μmin=μg-4σg，μmax=μg+4σg以及σg;对于优化随机逼近方法，取x1=μg，β=1/σg，τ1=3.039 8.在实际应用中，根据经验可以将x1设置在μ(即真实临界隔板厚度)附近，然而对σ 的猜测偏差较大。所以，借鉴文献［8］，取x1=8，10，12，σg=0.5，1，2，3.在x1和σg的各种组合下，应用蒙特卡洛方法模拟样本量为n 的升降法、Neyer 方法以及优化随机逼近方法试验数据。根据升降法和Neyer 方法试验数据求出μ 的极大似然估计，根据优化随机逼近试验数据用xn+1估计μ.将模拟过程重复1 000 次，获得参数μ 的估计各1 000 个。分别计算3 种方法所得估计的偏差和MSE［9］(即各个估计相对于真实临界隔板厚度的波动性)。表3和表4分别展示了在n=10 和20 两种情形下，应用3 种方法所得到的临界隔板厚度估计的MSE1/2.图1～图6则展示了在这两种情形下，应用3 种方法所得到的临界隔板厚度估计的平均值与真实临界隔板厚度μ 之间的偏差。

表5 样本量为10 时升降法、Neyer 方法和本文方法估计临界隔板厚度的MSE1/2Tab.5 The (MSE)1/2 of estimation using Up-and-Down Neyer and the New method when the sample size is 10

表6 样本量为20 时应用升降法、Neyer 方法和本文方法估计临界隔板厚度的MSE1/2Tab.6 The (MSE)1/2 of estimation using Up-and-Down Neyer and the New method when the sample size is 20

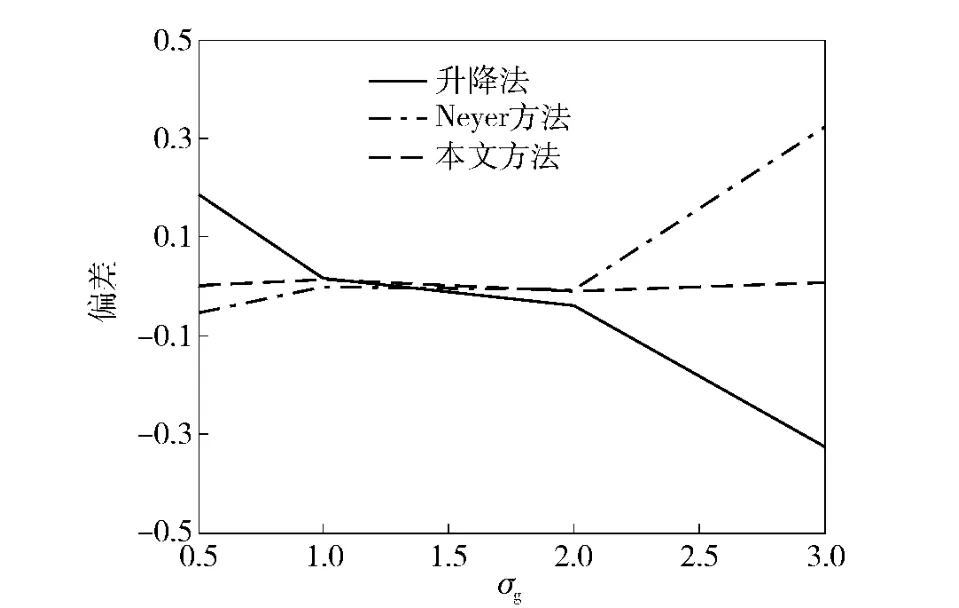
图1 样本量n=10 和μg =8 时估计的偏差Fig.1 The bias of estimation when n=10，μg =8

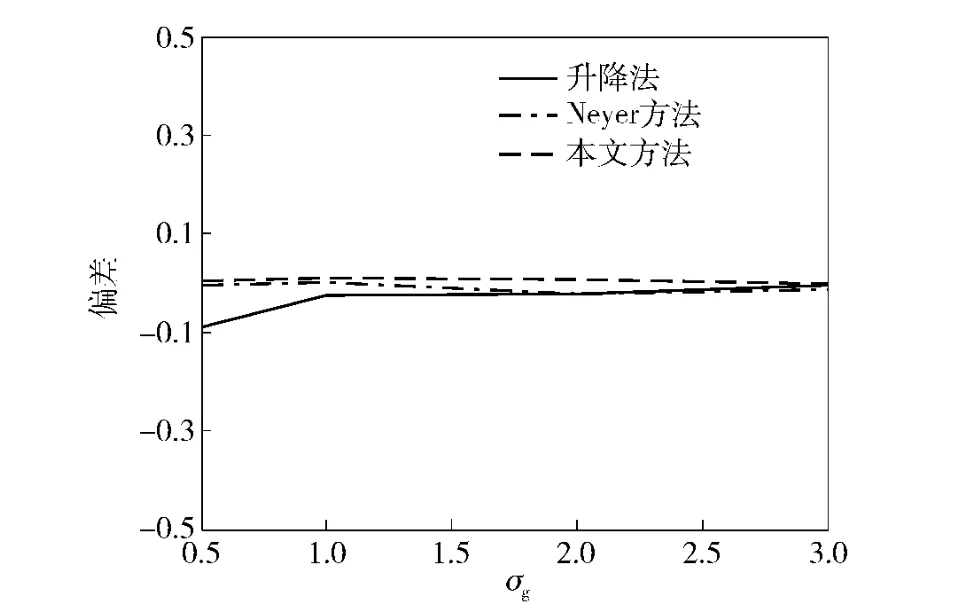
图2 样本量n=10 和μg =10 时估计的偏差Fig.2 The bias of estimation when n=10，μg =10

从表3和表4以及图1～图6的模拟结果不难发现，应用本文方法估计临界隔板厚度，估计更稳健(MSE 小)，并且更接近真值。接下来，将本文提出的新方法应用于实际试验，研究它的实际应用效果。

3 实际应用

用本文提出的优化随机逼近方法，测定某种炸药临界起爆的铝隔板厚度，并与以往升降法测定的试验数据进行比较。由于试验条件的限制，铝隔板的厚度只能以0.5 mm 的幅度进行增减，因此在试验过程中，对试验水平进行了截断调整。具体的调整方法为

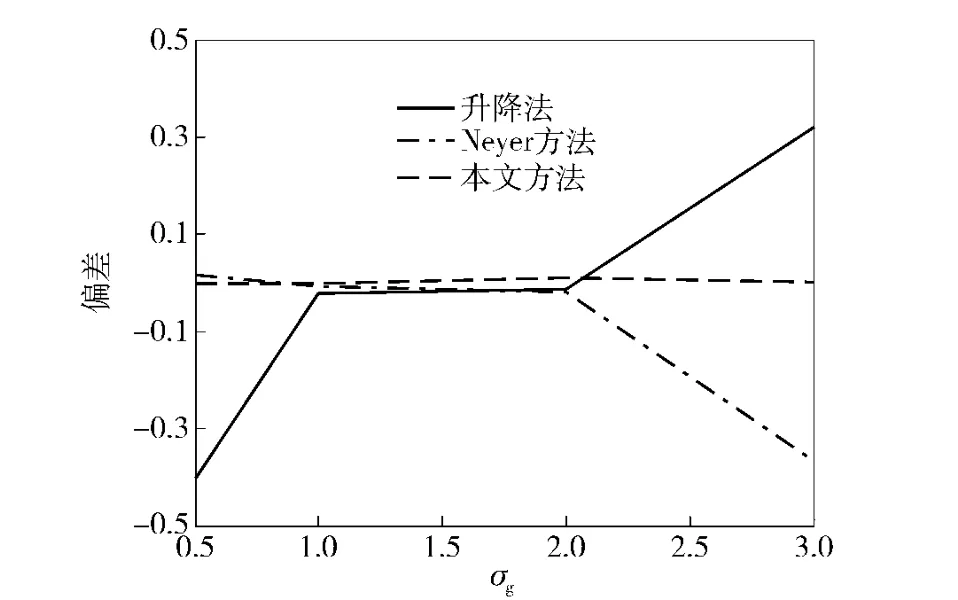
图3 样本量n=10 和μg =12 时估计的偏差Fig.3 The bias of estimation when n=10，μg =12

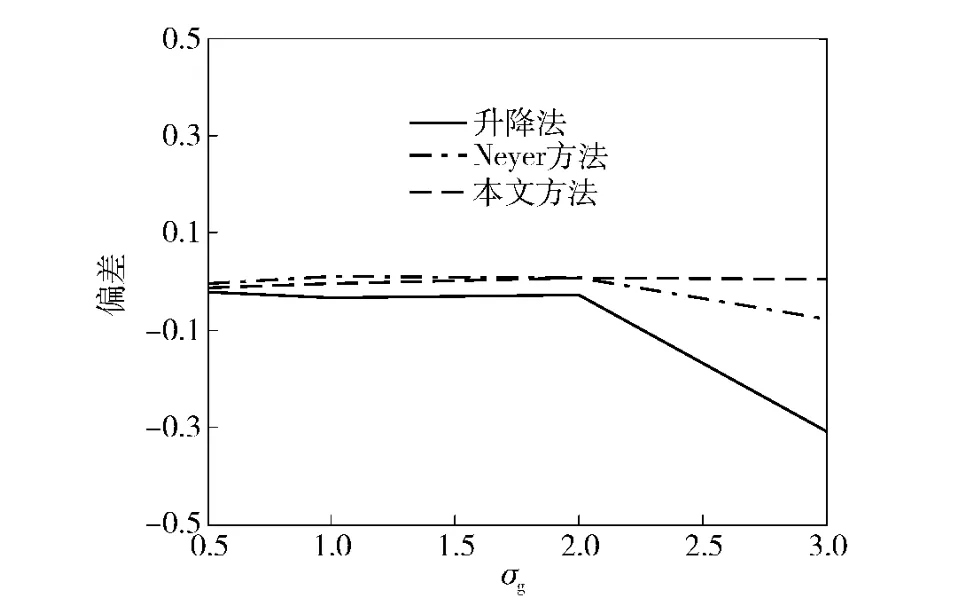
图4 样本量n=20 和μg =8 时估计的偏差Fig.4 The bias of estimation when n=20，μg =8

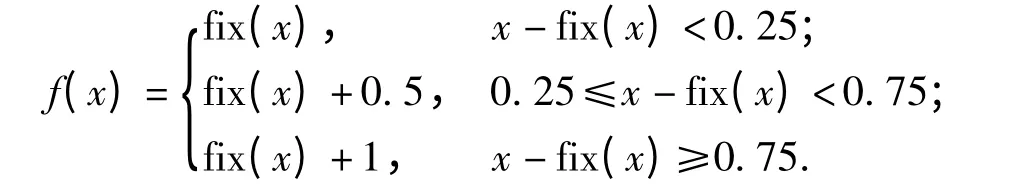
式中fix(x)表示绝对值不超过|x|的整数。

应用优化随机逼近方法，用16 发样本得到铝隔板的临界起爆厚度为27 mm，具体试验结果见表7.以往的两组升降法(各20 发样本)得到的铝隔板临界起爆厚度均值为27.11 mm(两次临界隔板厚度的估计分别为:26.92 mm 和27.30 mm).从估计结果来看，优化随机逼近方法(16 发样本)所得估计与两组升降法(20 发样本)所得估计的均值更接近，进一步表明优化随机逼近方法的精确性。同时也将优化随机逼近方法应用于其它两组空气间隙试验，具体试验数据见表8和表9.从试验结果可以发现，用较小的样本量达到了收敛效果。

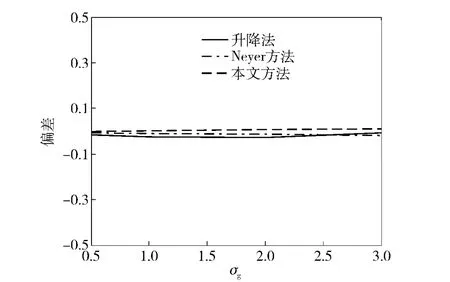
图5 样本量n=20 和μg =10 时估计的偏差Fig.5 The bias of estimation when n=20，μg =10

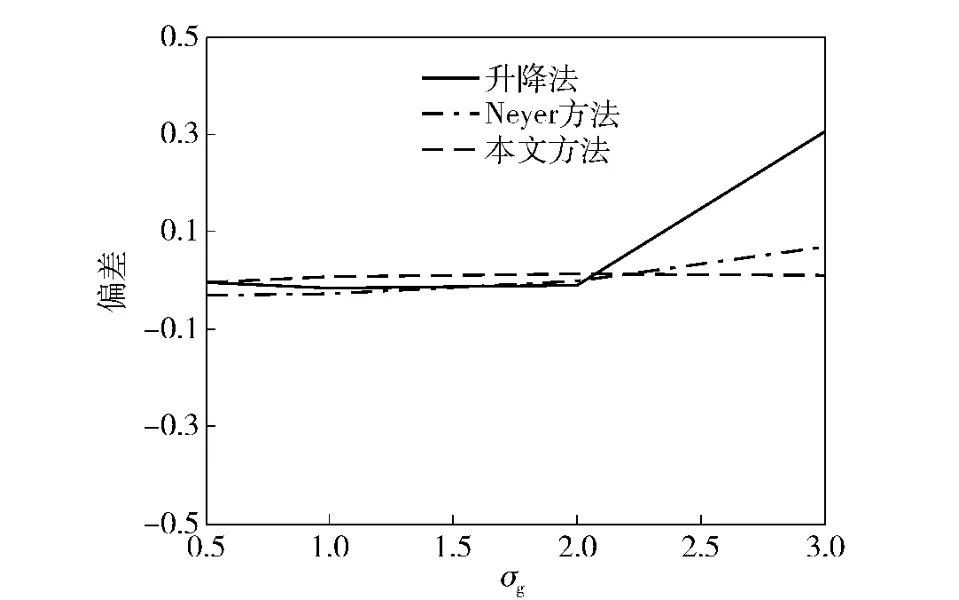
图6 样本量n=20 和μg =12 时估计的偏差Fig.6 The bias of estimation when n=20，μg =12

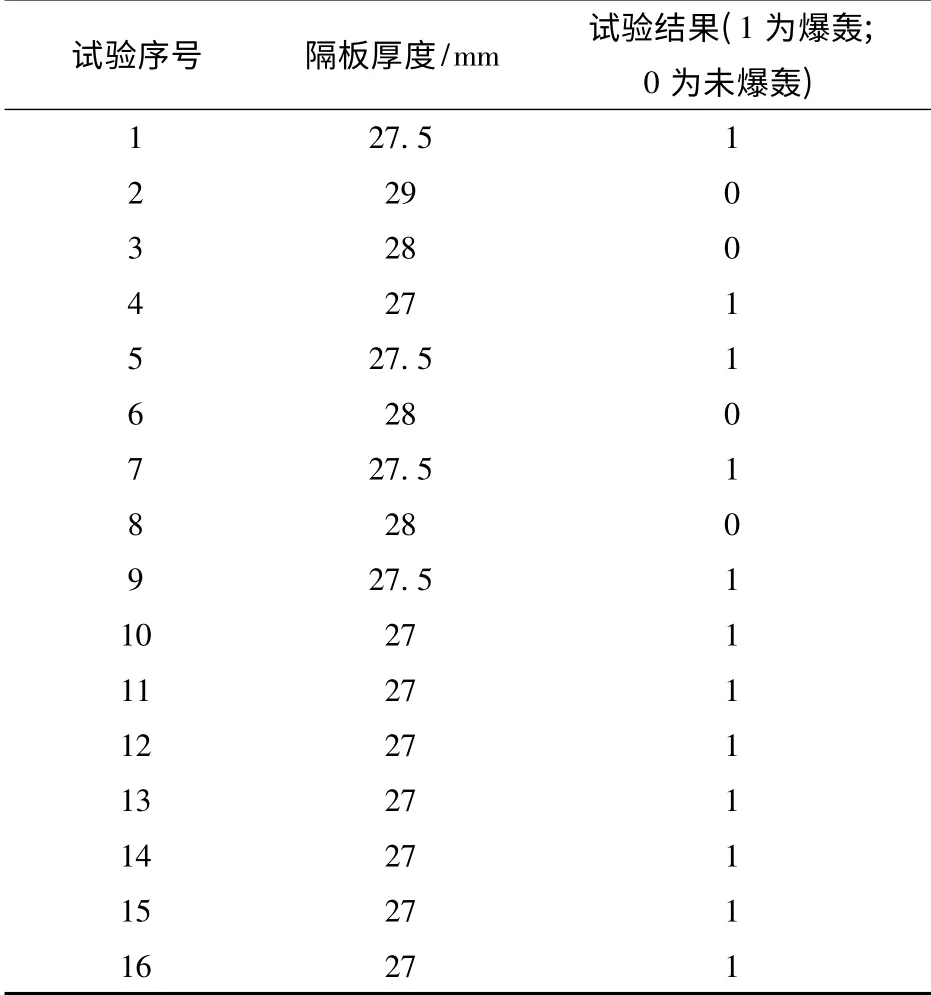
表7 优化随机逼近方法估计铝隔板临界起爆厚度的实际试验数据Tab.7 The experiment data using new method to estimate the critical gap thickness

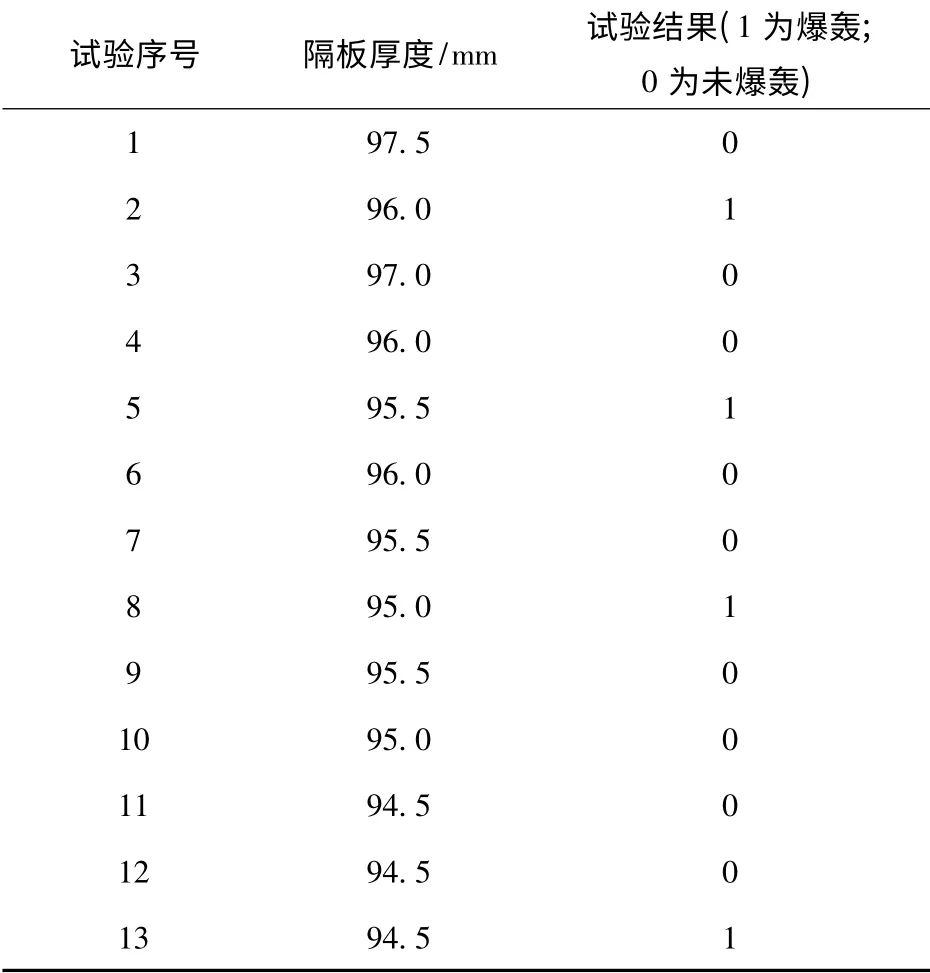
表8 优化随机逼近方法估计空气间隙(低密度药柱)的实际试验数据Tab.8 The experiment data using new method to estimate the critical air gap (low density medicine column)

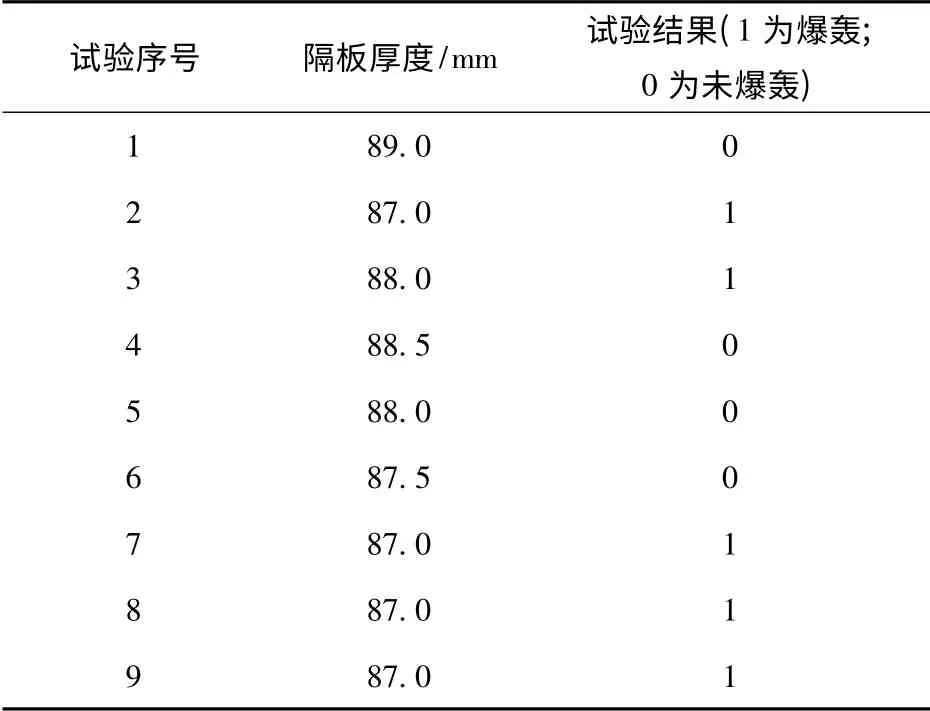
表9 优化随机逼近方法估计空气间隙(高密度药柱)的实际试验数据Tab.9 The experiment data using new method to estimate the critical air gap (high density medicine column)

4 结论

从表1～表2的模拟数据可以看出在步长或者σ 猜测较大的时候，升降法的无效试验和Neyer 方法的无效试验比率急剧增多，造成了试验的浪费和不确定性;而本文所提出的优化随机逼近方法采用的是序贯逼近策略，不使用似然方法，避免了无效试验的情况。从表3和表4以及图1～图6不难发现，应用本文方法估计临界隔板厚度，估计的稳健性大多优于升降法和Neyer 方法，并且更接近真值。因此，可以认为本文提出的优化随机逼近方法比国军标GJB/Z377A—94 中的升降法优越，是一种估计火工品和火炸药感度以及其他临界值的优化小样本试验设计方法。

References)

［1］ 陈文，胡晓东.某新型炸药冲击起爆试验与临界起爆特性研究［J］.火工品，2009，(2):5 -8.CHEN Wen，HU Xiao-dong.Experimental study on impact initiation characteristic of a new explosive［J］.Initiator＆Pyrotechnics，2009，(2):5 -8.(in Chinese)

［2］ 王金英，张景林.PBXN—5 传爆药安全可靠性试验方法研究［J］.中国安全科学学报，2010，20(1):72 -76.WANG Jin-ying，ZHANG Jing-lin.Experimental study on the reliability and safety of PBXN—5 booster［J］.China Safety Science Journal，2010，20(1):72 -76.(in Chinese)

［3］ 国防科学技术工业委员会.GJB/Z377A—94 感度试验用数据统计方法［S］.北京:中国标准出版社，1995.Commission of Science Technology and Industry for National Defense.GJB/Z377A—94 Statistical method for sensitivity test［S］.Beijing:China Zhijian Publishing House，1995.(in Chinese)

［4］ 王作山，张景林，刘玉存.纳米Al2O3对HMX 临界起爆压力的影响［J］.测试技术学报，2005，19(2):152 -156.WANG Zuo-shan，ZHANG Jing-lin，LIU Yu-cun.The effect of Nano-Al2O3on critical initiation pressure of HMX［J］.Journal of Test and Measurement Technology，2005，19(2):152 -156.(in Chinese)

［5］ Silvapulle M J.On the existence of maximum likelihood estimators for the binomial response model［J］.Journal of the Royal Statistical Society，Ser.B，1981，43:310 -313.

［6］ Neyer B T.A D-optimality-based sensitivity test［J］.Technometrics，1994，36:61 -70.

［7］ Joseph V R.Efficient Robbins-Monro procedure for binary data［J］.Biometrika，2004，91:461 -470.

［8］ 田玉斌，王典朋，房永飞.火工品发火点估计方法比较研究［J］.Chinese Journal of Energetic Materials，2010，18(1):58 -62.TIAN Yu-bin，WANG Dian-peng，FANG Yong-fei.Comparative study on estimating method of firing level of pyrotechnics［J］.Chinese Journal of Energetic Materials，2010，18(1):58 -62.(in Chinese)

［9］ 严楠.感度试验设计方法的若干研究［D］.北京:北京理工大学，1996.YAN Nan.Studies on sensitivity experimental design methods［D］.Beijing:Beijing Institute of Technology，1996.(in Chinese)