高超声速飞行器的动态滑模飞行控制器设计

耿洁，刘向东，王亮

(北京理工大学自动化学院，北京100081)

0 引言

高超声速飞行器飞行跨度范围大，飞行环境复杂多变，且飞行器机身与推进系统严重耦合［1］，高速飞行使得此类飞行器对外形和空气动态参数以及大气条件的变化非常敏感。另外，在高超声速条件下，风洞试验地面设备不足以及飞行测试的困难，导致其大气特性和气动特征难以量测和估计。以上特点均导致了飞行器模型中存在不确定性，鉴于模型的不确定性对高超声速飞行器的控制系统具有很强的不利作用，因此，高精度，高鲁棒性的控制方法设计一直是高超声速飞行器动态特性及其控制研究的主要目标。

滑模控制作为一种变结构控制方法对满足匹配条件的外部扰动和参数不确定性不敏感，是解决高超声速飞行器控制器设计的一个较好方法。然而，传统的普通滑模控制存在抖振现象，限制了其发展与应用。目前，已经提出了消除滑模控制抖振问题的多种方法。其中比较典型的是边界层法，即采用连续的函数(饱和函数或sigmoid 函数等)来替代产生切换控制动作的符号函数或者不连续的控制量，但边界层的引入降低了系统的控制精度。目前采用更多的是动态滑模方法［2］以及高阶滑模方法［3］。动态滑模或者高阶滑模能够产生连续的控制量以及更高的控制精度，同时又保留了传统滑模控制所具有的优点，能有效地减少抖振并提高系统的控制精度。

本文针对高超声速飞行器纵向模型来研究动态滑模飞行控制器的设计问题。

1 高超声速飞行器纵向动力学模型

本文采用通用高超声速飞行器在平稳巡航条件下的纵向模型［4］:

式中:v 为速度;γ 为飞行路径角;h 为高度;α 为攻角;q 为俯仰角速率;m 为飞行器质量;ρ 为空气密度;A 为参考面积;CL、CD、CT分别为升力系数、阻力系数、推力系数:CL=0.620 3α，CD=0.645 0α2+0.004 337α + 0.003 772， CT=升力L =0.5ρv2ACL;阻力D=0.5ρv2ACD;推力T=0.5ρv2ACT.

CM(α)、CM(q)、CM(δe)分别是由于攻角、俯仰角速率、升降舵偏角产生的力矩系数:

俯仰力矩:

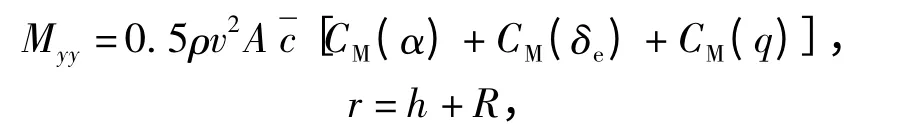
发动机动态方程采用典型二阶系统模型:

式中:β 为发动机的节流阀给定;βc为节流阀给定的指令信号。

在假定的参数标称值中加入随机变化量来表示参数的不确定性:

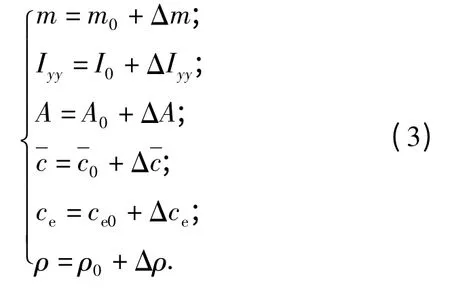
式中，m0，I0，A0，ce0，ρ0分别表示为高超声速飞行器相关参数的标称值。

2 模型线性化处理

在高超声速飞行器巡航段，期望的飞行器速度和高度分别为vd与hd，速度和高度误差分别为eV=v－vd，eH=h－hd.其控制任务是通过控制输入升降舵偏转角δe和发动机的节流阀给定βc的调节，最终使误差eV和eH为0，使得飞行器按照设定的高度和速度巡航飞行。

针对(1)式表示的高超声速飞行器纵向模型，运用全状态反馈进行输入/输出线性化，对输出飞行速度v 和高度h 分别微分n 次和m 次，直到控制输入升降舵偏转角δe和发动机的节流阀给定βc出现在微分式子中:

可见，经过对v 三次微分和对h 四次微分可以得出控制输入量。且:

进而输出动力学方程能够写成

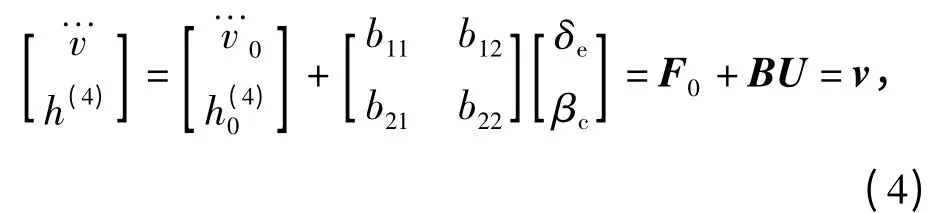
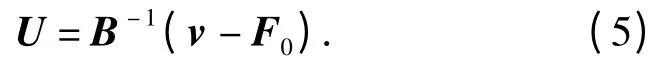
考虑(3)式所示的模型不确定性，由于参数ρ与s 总是一起出现在飞行器的动态方程中，因而将这2 个参数合并为ρA，从而定义参数向量p=［ρAce1/m 1/Iyy］，则参数向量p 的不确定部分相应表示为Δp=［ΔρAΔce1/Δm 1/ΔIyy］.

在对飞行速度v 和高度h 用全状态反馈进行线性化处理过程中，考虑上述参数不确定性，可得到

ΔWi(Δp)，i=1，2 为不确定参数的组合。不确定参数偏离标称值较小，为了简化计算，可进行在标称值附近的泰勒展开，并且忽略高阶项进行估算。

因而根据(6)～(8)式，可将(4)式转化为

式中ΔF0+ΔBU=Δv=(v1v2)T.

假定Δv 有界:|Δvi|≤Ψvi，其中i=1，2.

经过以上步骤后，根据转化后的模型，即(9)式进行动态滑模控制器设计。

3 动态滑模控制器设计

下面具体讨论动态滑模跟踪控制器设计过程，并给出满足系统稳定的参数设计范围.控制系统的设计问题主要是选择矢量［βcδe］T，使速度v 和高度h 跟随给定的期望值vd与hd.经过反馈线性化，系统实现了输入输出解耦，可以对速度通道和高度通道分别设计控制器。定义传统滑模面:

式中:S 为滑模面数组;数组元素SV、SH分别为速度通道、高度通道的滑模面;滑模斜率λV、λH为正常数。

对时间求导可得

式中:ρ1V，ρ2V＞0;ρ1H，ρ2H＞0.这样就得到了整个动态滑模控制器的结构模型。很明显，辅助变量χ =［χVχH］T可看作是前面定义的2 个滑模函数S 和J 的误差。需要研究的问题就是设计一个合适的控制量来保证辅助滑模函数J－滑模的存在和收敛。

为了得到满足滑模函数有限时间收敛的控制量，首先，引入引理1［5－6］.

引理1 对于如下(14)式所示微分方程的解及其导数将在有限时间内收敛到0，

根据引理1，进一步提出定理1 来证明动态滑模控制器各滑模平面的收敛性。

定理1 考虑如(1)式描述的高超声速纵向模型，设计传统滑模平面(10)式，同时构造辅助滑模平面(13)式，如果动态滑模控制律取为(15)式所示的形式:

式中:ρ3V＞0;ρ3H＞0.同时控制器参数满足(16)～(19)式所示的条件:

整个证明过程可分为2 步:

1)辅助滑模平面J 的有限时间收敛性。首先证明JV的有限时间收敛性，参考(11)式中的表达式，由于Vd为常数，所以=0，由于，有界，λV是正常数，所以，存在正常数C1，使|2λV+|≤C1.

同时，关于辅助滑模平面JV的动态方程将变成如下形式:

将方程(13)式、(15)式代入(20)式，可得:

所以，

且

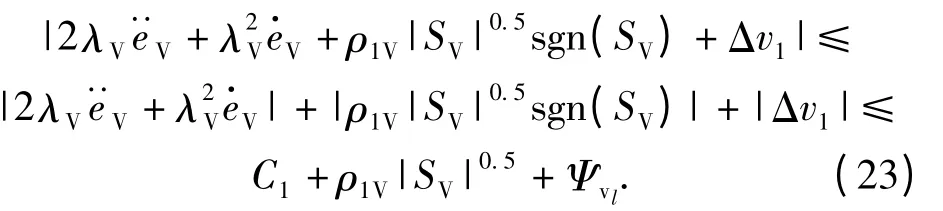
比较方程(23)式和(14)式，并根据引理1，可得到，如果动态滑模控制器参数满足(16)～(17)式所示的不等式条件，那么辅助滑模平面JV将在有限时间tJV内收敛到0，即

根据成都市医疗废物处置中心项目二期厂房及拟建停车场规划方案，修建二期厂房后边坡需开挖，受场地用地条件限制，边坡需采用直立开挖，开挖后形成13m高（P2边坡）和7m高（P1边坡）两个工程边坡，P1工程边坡位于P2工程边坡上方，距离约22～29m。P1工程边坡开挖岩土体主要含角砾粉质粘土及回填土组成，边坡可能会沿着基覆交界面的含角砾粉质粘土中薄层灰白色夹紫红色粉质粘土剪出；P2工程开挖边坡主要由风化基岩组成，边坡会沿着层间结构面及层间错动带等软弱结构面剪出。

取tJ=max(tJV，tJH)，则J 在有限时间tJ内收敛到0.

2)传统滑模平面S 的收敛性。当经过tJ这段时间后，由于J(t≥tJ)=0，因此，由(12)～(13)式可得

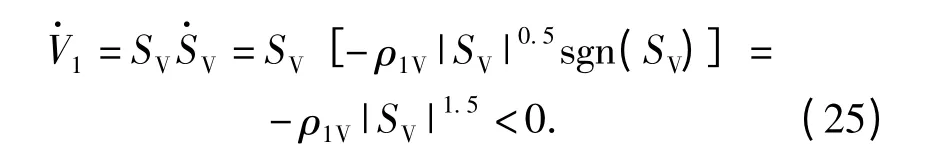
求解上述微分方程，可得

因此，可得出结论，滑模函数SV在有限时间内，有v1(t≥tSV)=0，同样，对 SH，可得到有效收敛时间 tSH=，取tS= max(tSV，tSH)，至此，我们可以得出结论:传统的滑模平面S 以及辅助的滑模平面J 都是有限时间收敛的。并且辅助滑模平面的收敛速度要大于传统的滑模平面，即有

［7］给出滑模面J 先于S 收敛的初始条件:

在仿真中取合适的参数可保证该条件满足。

证毕。

从上面的证明过程可以看出，动态滑模控制器的滑模平面是分两阶段收敛的，先是辅助滑模平面J 在有限时间内收敛到0，然后是传统滑模平面S 再经过有限时间收敛到0.

由上面的定理可知，经过时间tS，S =0 恒成立，解下列微分方程可得到误差随时间的变化规律:

4 仿真实验分析

运用MATLAB 的Simulink 仿真工具进行33 528 m高度和马赫数15 的飞行条件下高超声速飞行器控制仿真实验，此时飞行器的平衡状态为:v0=4 590.3 m/s，h0=33 528 m，γ0=0°，q0=0° ，α0=2.92°.高超声速飞行器模型参数参考文献［8］.选择滑模斜率λV=λH=0.3，以及动态滑模参数ρ1V=5，ρ2V= 150，ρ3V= 1 000，ρ1H= 5，ρ2H= 150，ρ3H=1 000.初始误差取eV(0)=－40 m/s，eH(0)=－60 m，JV(0)=－ 3.8，JH(0)=－ 2.0，SV(0)=－3.8，SH(0)=－2.0，满足(27)式所示条件。

图1比较了标称模型情况下分别运用动态滑模与普通滑模进行控制的仿真结果。

为了检验动态滑模控制器的鲁棒性，在标称模型中引入参数不确定性，将普通滑模与动态滑模的仿真结果进行比较。仿真中选取飞行器纵向模型的不确定参数的变化，如(22)式。并将普通滑模与动态滑模的仿真结果进行比较，如图2所示。

可看出，对于标称模型，普通滑模与动态滑模都可以实现较好的控制，采用动态滑模控制器时响应速度有一定程度的提高，当模型具有参数不确定性时，普通滑模的控制性能受到较大影响，高度响应速度明显降低，需要40 s 才能跟上给定高度信号。但是动态滑模依然能够保持较好的控制响应，与普通滑模相比，动态滑模可以缩短调节时间。所以，对于具有模型参数不确定性的情况，动态滑模具有明显的优势。

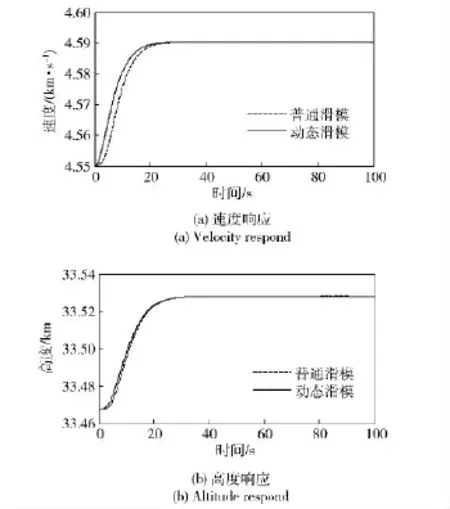
图1 标称模型对马赫数为15 的速度指令和33 528 m的高度指令的响应Fig.1 Respond to Mach 15 step velocity command and 33 528 m step altitude command with common and dynamic sliding mode controllers for nominal model

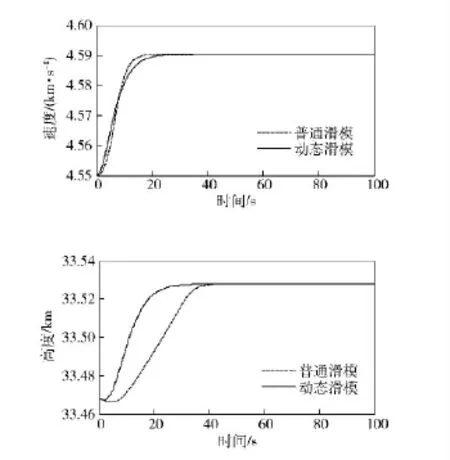
图2 最大参数不确定性情况下动态滑模和普通滑模对马赫数为15 的速度阶跃指令和33 528 m 的高度阶跃指令的响应Fig.2 Respond to Mach 15 step velocity command and 33 528 m step altitude command with common and dynamic sliding mode controllers when using largest parameter uncertainties

如图3所示，模型具有最大参数不确定性时动态滑模面SV、SH与普通滑模面SVC、SHC收敛情况的对比。可看出，普通滑模的到达时间明显比动态滑模要长。

图3 动态滑模与普通滑模方法的滑模面对比Fig.3 The slide surface of common and dynamic sliding mode controllers

图4 动态滑模与普通滑模的控制量对比Fig.4 The controlled variables for common and dynamic sliding mode controllers

如图4所示，比较了动态滑模与普通滑模的控制量。采用动态滑模后，控制量的抖动明显减小了。

5 结论

本文针对通用高超声速飞行器纵向模型提出了一种动态滑模跟踪控制方法。首先采用了输入输出反馈线性化，将该模型转化为仿射型，然后引入辅助滑模面，实现了动态滑模面的两阶段有限时间收敛。动态滑模在保留普通滑模控制优点的同时对不连续的控制量输出加以积分作用，有效地降低了普通滑模的抖振现象。仿真结果验证了提出方法的有效性和鲁棒性。

参考文献(References)

［1］ 朱云骥，史忠科.高超声速飞行器飞行特性和控制的若干问题［J］.飞行力学，2005，23(3):5－8.ZHU Yun－ji，SHI Zhong－ke.Several problems of flight characteristics and flight control for hypersonic vehicles［J］.Flight Dynamics，2005，23(3):5－8.(in Chinese)

［2］ Yan X G，Spurgeon S K，Edwards C.Dynamic sliding mode control for a class of systems with mismatched uncertainty［J］.European Journal of Control，2005，11(1):1－10.

［3］ Garc L G，Parra V，Arteaga M A.Higher－order sliding mode impedance bilateral teleoperation with robust state estimation under constant unknown time delay［C］∥Proceedings of the 2005 IEEE/ASME International Conference on Advanced Intelligent Mechatronics.California:ASME，2005:1293－1298.

［4］ Xu H J，Ioannou P A，Mirmirani M.Adaptive sliding mode control design fora hypersonic flight vehicle［J］.Journal of Guidance，Control and Dynamics，2004，25(5):829－838.

［5］ Kaveh P，Ashrafi A，Shtessel Y.Integral and second order sliding mode control of harmonic［C］∥Proceedings of the 44th IEEE Conference on Decision and Control，and the European Control Conference.Spain:IEEE，2005:3941－3946.

［6］ Tournes C H，Frederick R，Carroll T，et al.Miniature interceptor guidance and control using second order sliding mode and adaptive control［C］∥AIAA Guidance，Navigation，and Control Conference and Exhibit.San Francisco:AIAA，2005:1－15.

［7］ Koshkouei A J，Burnham K J，Zinober A S I.Dynamic sliding mode control design［J］.Control Theory and Applications，2005，152(4):392－396.

［8］ Xu H，Leung P，Mirmirani M，et al.Adaptive sliding mode control of a hypersonic flight vehicle［C］∥Proceeding of the 11th Annual AAS/AIAA Space Flight Mechanics Meeting.Santa Barbara:CSA，2001:1947－1961.