固体火箭发动机药柱概率贮存寿命预估

唐国金，申志彬，田四朋，杨东

(1.国防科学技术大学 航天与材料工程学院，湖南 长沙410073;2.成都飞机设计研究所，四川 成都610041;3.中国航天科技集团公司 四院43 所，陕西 西安710025)

0 引言

固体火箭发动机(SRM)药柱贮存寿命预估具有重要意义。常规的药柱贮存寿命预估一般采用“确定性模型”，不考虑随机参数的影响，取其均值进行分析。这降低了预估的准确度和可信度，是预估寿命偏离真实寿命的重要原因之一。

20世纪60年代初，文献［1］采用数理统计方法和应力－强度干涉理论处理随机因素，初步形成了概率寿命预估的思想。文献［2－3］基于高温加速老化试验，分析了固体推进剂的可靠贮存寿命。上述研究仅以固体推进剂力学性能参数作为发动机贮存寿命的标志参数，脱离了药柱真实几何形状和载荷历程，不可避免存在较大的误差。文献［4－5］将发动机药柱简化为一个弹性约束的无限长中空圆筒，利用经验公式和Monte Carlo 方法进行随机结构分析，得到了药柱结构可靠度随贮存时间的变化。文献［6］则采用粘弹性Monte Carlo 随机有限元法对随机温度载荷下导弹结构进行了概率贮存寿命预估。但由于计算手段和分析方法的限制，这些研究仅能处理一些简化的药柱模型，难以应用于实际工程问题。预估具体发动机药柱的概率贮存寿命，需借助三维粘弹性随机有限元法，目前尚无采用该方法开展SRM 概率贮存寿命预估的研究报道。

本文基于三维粘弹性随机有限元法和推进剂高温加速老化试验，对某SRM 药柱的概率贮存寿命进行预估。

1 概率寿命预估模型

高温加速老化试验数据符合统计原则，假设总体服从正态分布，各观察值之间相互独立［7］。加速老化过程中，固体推进剂某些性能参数的变化与时间、温度存在一定的相关关系，通过对老化数据进行拟合，可找到一个与其相适应的老化模型方程。航天行业标准QJ 2328A—2005［7］给出了用于数据处理的3 个老化模型:

式中:I 为固体推进剂某一时刻的性能;I0为性能初始值(常数);K 为与温度有关的性能变化速度常数;t 为老化时间，单位:周。

在老化过程中，假定固体推进剂性能变化服从Arrhenius 化学动力学方程:

式中:E 为活化能;H 为频率因子;R 为气体常数。

考虑预测过程中存在的随机误差，需求K 的置信界限。先求lnK 的标准差［7］

于是，(4)式的置信界限为

式中tα为置信概率为1－α 时t 分布值。

从而可得贮存温度为Ts时，K 的上限值

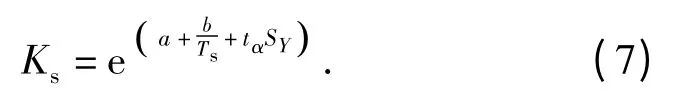
根据文献［7］，可取各老化试验温度下初始性能的平均值为(1)～(3)式的性能初始值，即

固体发动机结构可靠度

式中:Zp(t)为某时刻药柱的功能函数;R(t)和S(t)分别为该时刻与强度和结构响应有关的随机参数。假定R(t)和S(t)均为简单随机变量，服从正态分布且相互独立，则Zp亦服从正态分布，其均值和方差分别为

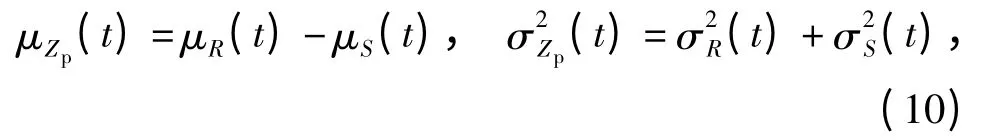
式中:μR(t)、μS(t)和σ2R(t)、σ2S(t)分别为R(t)、S(t)的均值和方差。对(9)式进行标准化变换，则［8］

式中Φ(·)为标准正态分布的累积分布函数。

失效概率

结构可靠度分析中，通常令

β(t)即可靠指标。不难看出，在R(t)和S(t)均为正态分布的条件下，β(t)唯一确定了结构可靠度。

本文药柱的破坏准则采用与八面体剪应变等效Von Mises 应变准则［9］，因此，R(t)和S(t)分别表示某贮存时间推进剂的最大伸长率和药柱的最大Von Mises 应变。按照(11)～(13)式给出的可靠度分析模型，可得药柱结构可靠度随贮存时间的变化规律，进一步可求取满足一定可靠度要求的概率贮存寿命。

以可靠指标β 为例，给出基于可靠指标的药柱概率寿命预估模型。对各个贮存期的药柱进行随机结构完整性分析得到药柱最大Von Mises 应变均值μS和标准差σS，结合推进剂最大伸长率各贮存时间的均值μR和标准差σR.利用(13)式可得药柱各贮存期的可靠指标β(t)，对其进行参数拟合得

β(t)与推进剂材料参数M，药柱载荷参数L，几何参数G，贮存温度T 以及贮存时间t 有关，其中M、L、G和T 为参数，t 为变量。f(M，L，T，t)可以为多项式模型、指数模型或对数模型。给定满足要求的可靠指标β0，利用(14)式便可得到一定可靠指标下药柱的贮存寿命t.(14)式即为基于可靠指标的药柱概率寿命预估模型。同理，利用(11)～(12)式可得基于可靠度和失效概率的药柱概率寿命预估模型。

2 概率寿命预估流程

采用基于高温加速老化试验和结构完整性分析相结合的药柱寿命预估方法［9］，利用三维粘弹性随机有限元方法，对SRM 药柱进行概率寿命预估，流程如图1所示。本文采用三维粘弹性响应面随机有限元法对药柱进行随机结构分析［10］，基于Von Mises 应变准则计算药柱的结构可靠度。

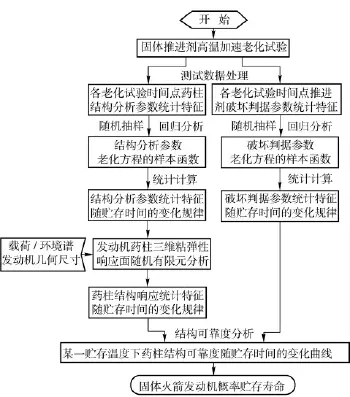
图1 药柱概率贮存寿命预估流程Fig.1 Flow chart of grain probabilistic storage life prediction

3 算例

利用提出的概率寿命预估模型对某固体发动机药柱进行概率寿命预估。

3.1 试验方法

依照文献［7］对某HTPB 固体推进剂进行了高温加速老化试验，选取了40 ℃、50 ℃、60 ℃、70 ℃四个老化试验温度，每个老化温度下取样8 次。按照GB 4889—85 的要求，为了获取固体推进剂性能参数的统计特征，每次取样数目为25 个，并根据GJB 770B—2005 规定的方法对试件进行单向拉伸试验，异常数据按GB 4883—85 中规定的方法处理。由试验数据知，老化导致该推进剂最大伸长率降低，模量升高，且老化速度随老化温度升高加快。

3.2 老化性能统计特征随时间变化规律

按照文献［7］给出的原则，为了选择合适的老化数学模型，如图2～3 所示，给出了各老化温度下固体推进剂最大伸长率εmax及初始模量E0均值的散点图，并给出了一次多项式的最小二乘拟合曲线。

图2 最大伸长率均值与老化时间散点图Fig.2 Scatter diagram for specific elongation and aging time

图3 初始模量均值与老化时间散点图Fig.3 Scatter diagram for initial modulus and aging time

由散点图可看出，在各老化试验温度下，固体推进剂最大伸长率和初始模量的均值与老化时间具有明显的线性关系。为了进一步对线性相关性进行检验，如表1所示，列出了固体推进剂最大伸长率和初始模量均值随老化时间变化的回归方程，同时给出了线性相关系数和相应的置信概率。计算表明，在置信概率大于99%的条件下，该型号固体推进剂老化性能参数与老化时间的线性关系成立，因此可采用(1)式的老化模型方程求解各老化试验温度下的性能变化速度常数K，然后求解Arrhenius 方程中的其他系数，进而外推出常温贮存条件下固体推进剂的性能变化速度常数。

表1 固体推进剂老化性能参数随时间变化的回归方程Tab.1 Regression equation for propellant aging performance parameter variation with time

基于表1中给出的不同温度下性能变化速度常数，采用文献［7］给出的步骤对Arrhenius 方程(4)式中的参数进行计算及相关性检验，如表2所示。取置信概率为99%，有tα=4.540 7.从而在贮存温度Ts=25 ℃的条件下，可得固体推进剂最大伸长率εmax和初始模量E0的变化速度常数Ks的上限值分别为8.538 9 ×10－5和0.002 273.如表3所示，给出了固体推进剂性能变化的回归方程。

表2 老化温度与性能变化速度常数相关的回归方程Tab.2 Regression equation for performance velocity constant variation with aging temperature

这里从固体推进剂高温加速老化性能测试结果的均值出发给出了常温贮存条件下固体推进剂性能变化回归方程的计算过程，未考虑老化性能参数的随机性。实际上，由于不同老化温度和老化时间的性能参数具有随机性，在常温贮存条件下，固体推进剂性能参数必然随贮存时间随机变化，本文采用Monte Carlo 方法解决此问题，主要步骤为:1)对不同老化温度和老化试验时间的性能测试数据进行n次随机抽样;2)重复进行以上计算，可得到n 条常温贮存下固体推进剂性能变化的回归方程(样本函数);3)统计分析各回归方程在不同贮存时间的函数值，即可得到固体推进剂性能参数统计特征随贮存时间的变化规律。

表3 常温贮存条件下固体推进剂性能变化的回归方程Tab.3 Regression equation for propellant performance parameter variation under normal temperature

取随机抽样次数n=10 000，经计算可得常温贮存条件下固体推进剂最大伸长率和初始模量标准差随贮存时间的变化曲线，如图4～5 所示。

图4 最大伸长率标准差随时间变化曲线Fig.4 Curve of specific elongation standard deviation variation with time

图5 初始模量标准差随时间变化曲线Fig.5 Curve of initial modulus standard deviation variation with time

计算表明，老化试验数据的随机性对推进剂性能变化回归方程的初值I0影响不大，但对性能变化速度常数K 影响非常显著，从而导致推进剂最大伸长率和初始模量标准差随贮存时间的增加而增大。

3.3 药柱概率寿命预估

以文献［10］中给出的SRM 为例，取贮存温度Ts=25 ℃，载荷工况为常温点火发射，如表4所示，给出了药柱未老化时的部分结构参数，其中，推进剂松弛模量Prony 级数的松弛时间τj= 4.303 5 ×10j－1，j=1，2，3.

为简化计算，本文仅考虑推进剂松弛模量和最大伸长率的老化特性，不考虑其他随机参数随贮存时间的变化。由于推进剂松弛模量Prony 级数中的各参数是由一组(多个试样)应力松弛试验确定的，不能通过简单的统计分析得到。本文采用张海联［11］给出的近似解法得到。固体推进剂初始模量的老化统计特征已在3.2 节给出，其他松弛模量老化统计特征不一一列出，仅给出未老化时推进剂药柱的松弛模量统计特征。

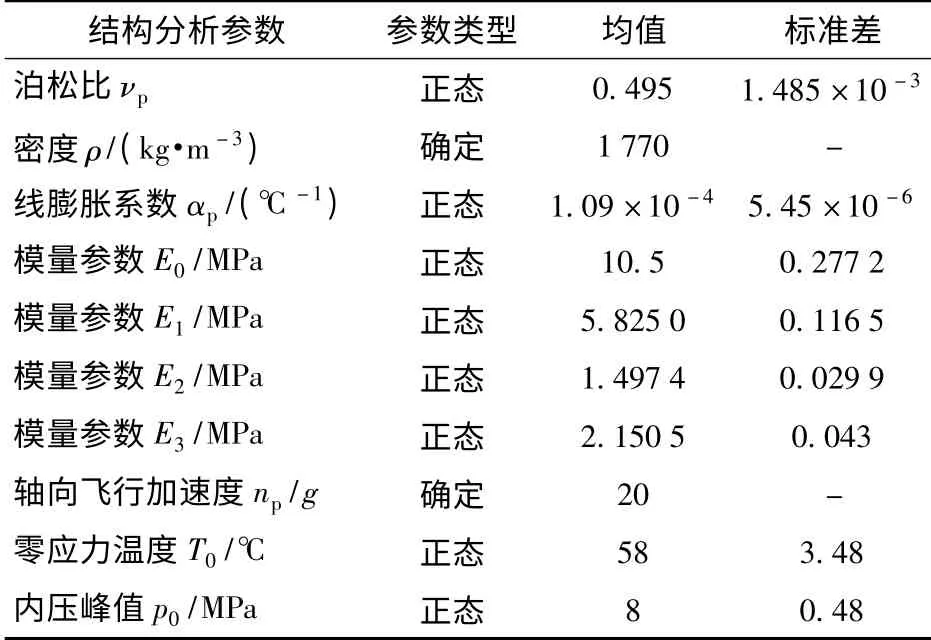
表4 药柱结构分析参数Tab.4 Structure analysis parameters of grain

采用响应面随机有限元方法对药柱进行随机结构完整性分析，假定贮存时间为20年，药柱危险点Von Mises 应变均值和标准差随贮存时间的变化曲线如图6～7 所示。可看出，随着贮存时间的增加，由于固体推进剂模量上升，SRM 药柱危险点Von Mises 应变的均值和标准差均有所下降。

利用(13)式计算各贮存时间药柱的可靠指标β，可得到药柱结构可靠指标随贮存时间的变化曲线，如图8所示，由图可知，在贮存期间SRM 药柱的结构可靠度不断降低，失效概率增加。如图9所示，进一步给出了药柱结构失效概率随贮存时间的变化曲线。

可见，根据药柱结构可靠度(或失效概率)随贮存时间的变化趋势，在不同结构可靠度水平下，可得到药柱不同的寿命预估结果。

图6 应变均值随贮存时间的变化曲线Fig.6 Curve of strain equally variation with storage time

图7 应变标准差随贮存时间的变化曲线Fig.7 Curve of strain standard deviation variation with storage time

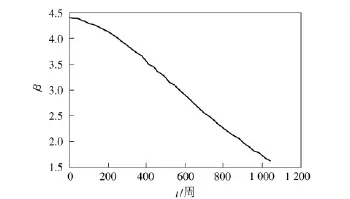
图8 药柱结构可靠指标随贮存时间的变化曲线Fig.8 Curve of grain structural reliable index variation with storage time

利用三次多项式模型对图8中数据点进行参数拟合，(14)式可表示为

式中:A0、A1、A2、A3分 别 为4.417、－ 7.032 × 10－4、－4.617×10－6、2.639 ×10－9，相关系数为0.999 9.给定β 或可靠度，就可从(15)式中求出药柱的概率寿命。如表5所示，给出了几种结构可靠度水平下该发动机药柱的贮存寿命。

图9 药柱失效概率随贮存时间的变化曲线Fig.9 Curve of grain failure probability variation with storage time

显然，在较高的结构可靠度水平条件下预估的贮存寿命较短，反之亦然。因此，确定合理的结构可靠度水平非常重要。

表5 SRM 药柱的概率贮存寿命Tab.5 Probabilistic storage life of solid rocket motor grain

4 结论

以三维粘弹性随机有限元法和固体推进剂高温加速老化试验为基础，提出了SRM 药柱概率贮存寿命预估模型，并实现了具体SRM 药柱的概率贮存寿命预估。主要研究结论如下:

1)基于粘弹性随机有限元法的SRM 药柱概率贮存寿命预估模型，能够综合考虑环境/载荷谱、几何构型及参数不确定性等因素对寿命预估的影响，结果更为合理、可信。

2)SRM 药柱概率贮存寿命预估能够在给定结构可靠度要求的条件下，给出药柱的贮存寿命。

3)对具体SRM 药柱进行概率贮存寿命预估，需借助三维粘弹性随机有限元法和结构可靠度分析理论。

本文建立和实现了适于工程应用的SRM 药柱概率贮存寿命预估模型，具有重要的理论意义和应用价值。

References)

［1］ Chappell R N，Jensen F R，Burton R W.Statistical service life prediction:minuteman third－stage propellant grain［J］.Journal of Spacecraft and Rockets，1968，5(1):42－46.

［2］ 刘德辉，贺南昌.复合推进剂贮存寿命及其可靠性研究［J］.推进技术，1993，14(6):63－67.LIU De－hui，HE Nan－chang.An investigation on storage life of composite propellant and its reliability［J］.Journal of Propulsion Technology，1993，14(6):63－67.(in Chinese)

［3］ 刘子如，郝仲璋，谢俊杰，等.FH－94 固体推进剂的可靠度评估和可靠贮存寿命预测研究［J］.兵工学报，1994，15(2):24－27.LIU Zi－ru，HAO Zhong－zhang，XIE Jun－jie，et al.Research on reliability evaluation and reliable life prediction of FH－94 solid propellant［J］.Acta Armamentarii，1994，15(2):24－27.(in Chinese)

［4］ Heller R A，Kamat M P.Service life prediction for solid propellant motors，AIAA－1978－486 ［R］.New York:American Institute of Aeronautics and Astronautics，1978.

［5］ Heller R A，Thangjitham S，Janajreh I M.Probabilistic service life prediction for solid propellant motors subjected to environmental thermal loads，AD－330303［R］.Virginia:Defence Technical Information Center，1997.

［6］ Cost T L.Probabilistic service life prediction of missile structures subjected to random thermal loads，AIAA－1980—406［R］.New York:American Institute of Aeronautics and Astronautics，1980.

［7］ 李彦丽，赵海泉，杜秋丽.QJ 2328A—2005 复合固体推进剂高温加速老化试验方法［S］.北京:中国航天标准化研究所，2005.LI Yan－li，ZHAO Hai－quan，DU Qiu－li.QJ 2328—2005 test method for temperature accelerated aging of composite solid propellant［S］.Beijing:China Astronautics Standards Institute，2005.(in Chinese)

［8］ 何水清，王善.结构可靠性分析与设计［M］.北京:国防工业出版社，1993.HE Shui－qing，WANG Shan.Structural reliability analysis and design［M］.Beijing:National Defense Industry Press，1993.(in Chinese)

［9］ 袁端才，唐国金，李海阳，等.基于加速老化与三维粘弹性有限元分析的固体导弹发动机寿命预估［J］.兵工学报，2006，27(4):685－689.YUAN Duan－cai，TANG Guo－jin，LI Hai－yang，et al.Three－dimension viscoelastic analysis and accelerated aging approach to predict the service life of solid missile motor［J］.Acta Armamentarii，2006，27(4):685－689.(in Chinese)

［10］ 田四朋.固体火箭发动机药柱三维粘弹性响应面随机有限元分析［J］.固体火箭技术，2010，33(1):17－20.TIAN Si－peng.Three－dimensional viscoelastic response surface stochastic finite element analysis on solid rocket motor grain［J］.Journal of Solid Rocket Technology，2010，33(1):17－20.(in Chinese)

［11］ 张海联.固体火箭发动机药柱的粘弹性不确定结构分析［D］.长沙:国防科学技术大学，2002.ZHANG Hai－lian.Viscoelastic uncertain structural analysis for solid rocket motor grain［D］.Changsha:National University of Defense Technology，2002.(in Chinese)