基于神经网络和遗传算法的卫星结构参数优化

韩 冲，陈 庆

（上海空间推进研究所，上海 200233）

对于卫星产品，追求更小的结构总质量和较高的一阶固有频率，一直是科技人员追求的目标。为了减轻卫星结构的总质量，通常有两种途径：一是对卫星结构进行优化设计；二是采用比模量和比强度高的复合材料代替传统的金属材料。

在复合材料工艺水平确定的情况下，优化设计显得尤为重要。在结构优化中，传统的有限元方法是重要方法之一。但是传统优化计算效率较低，优化过程参与了大量的有限元计算，耗时较多。如果变量设置不合理，往往陷入局部最优解的困境。

像整星结构这类单元较多的复杂结构，若直接采用商业软件进行优化，大量工作花费在了对分析文件的提取过程。如果是不熟悉软件语言的初学人员，将会遇到很大的挑战。因此需要探索新的优化方法，来完成优化工作。

本文尝试建立整星结构一阶固有频率最大、质量最小为目标的多目标优化设计模型，采用线性加权的方法，将多目标优化问题转换为单目标优化问题。结合正交实验技术，采用神经网络和遗传算法，在MATLAB软件平台上，完成整星结构的优化计算。

1 神经网络和遗传算法

1.1 神经网络

人工神经网络（Artificial Neural Networks，ANN），简称神经网络，作为对人脑最简单的一种抽象和模拟，是近年发展起来的一门十分活跃的交叉学科。理论证明，三层BP网络能映射任意的非线性函数，并且具有较好的全局收敛性与结构简单等优点。而针对卫星结构的设计参数与其固有频率的关系，亦是非线性关系，因此采用BP网络来映射从设计变量到目标函数的非线性关系，是比较合理的。图1所示为三层BP网络结构模型。

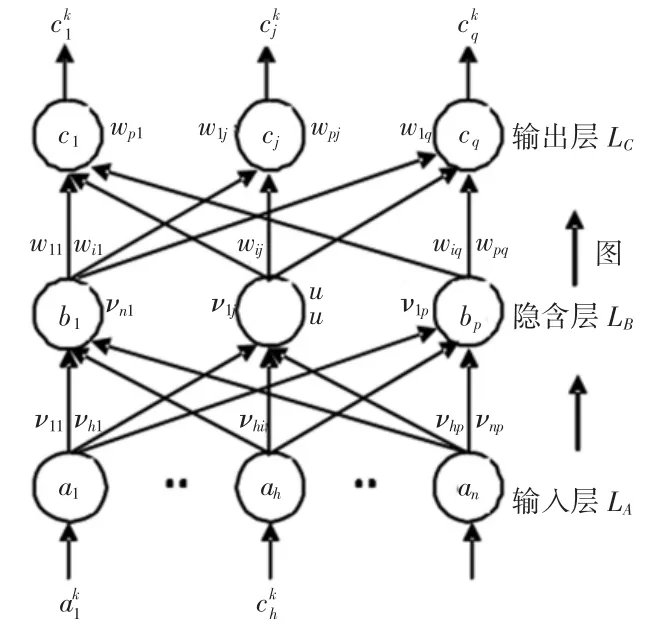
图1 三层BP网络示意图

1.2 遗传算法

遗传算法通过模拟自然界生物的进化过程来进行择优。其从代表问题的可能潜在解集的一个种群开始，而一个种群则是由经过基因编码的一定数目的个体组成。每个个体，实际上是染色体带有特征的实体。染色体作为遗传物质的主要载体，即多个基因的集合，其内部表现是某种基因组合，其决定了个体的外部表现。

在初始种群产生之后，按照适者生存和优胜劣汰的原理，逐代演化产生出越来越好的近似解。在每一代，根据问题域中个体的适应度大小挑选个体，并借助于自然遗传学的遗传算子进行组合交叉和变异，产生出代表新的解集的种群。这个过程导致种群像自然进化一样，后生代种群比前代种群更适应于环境，末代种群中的最优个体经过解码，可以作为问题的近似最优解。

遗传算法计算过程的实现，主要取决于变量编码、初始群体生成、适应度函数设计、遗传算子设计、算法控制参数选取、算法停止准则等环节设计。遗传算法流程图如图2所示。

图2 遗传算法流程图

2 应用与分析

2.1 优化模型

图3所示为某卫星结构图。

图3 卫星结构图

下面就是卫星整星结构多目标优化设计数学模型的目标函数：

式（1）中的 12 个自变量 x1，x2，…，x12表示相应的独立设计变量。

卫星整星结构优化模型可以描述如下：

式（2）中，

W为卫星结构总质量；

freq1是卫星结构一阶固有频率；

Tdi和T蜂窝芯分别对应蜂窝夹层板和蜂窝芯的失效公式；

umax为结构过载工况下的最大位移；

Mmax为相应材料的应力值；

Hi为蜂窝芯的厚度；

Lp为面板的厚度；

Rq为构架圆管的半径；

u0、M0和f0分别为卫星结构的各许用值。

2.2 优化设计变量参数组合表形成

本文的优化问题所涉及的参数和各参数的水平数不是太多，并且要将这些参数组合的计算结果，用于神经网络的训练。因此，参数的组合不能太少，并且要能反映出各个参数对计算结果的影响规律，本文采用正交实验选参法。各优化设计变量的水平数如下：

底板蜂窝芯子高度Hd：10～60 mm，在其变化范围内取6个水平数，增量为10 mm；

底板面板厚度Ld：0.2～1.0 mm，在其变化范围内取9个平均数，增量为0.1 mm；

层板蜂窝芯子高度Hc：10～60 mm，在其变化范围内取6个平均数，增量为10 mm；

层板面板厚度Lc：0.2～1.0 mm，在其变化范围内取9个平均数，增量为0.1 mm；

长立板蜂窝芯子高度Hl：10～60 mm，在其变化范围内取6个平均数，增量为10 mm；

长立板面板厚度Ll：0.2～1.0 mm，在其变化范围内取9个平均数，增量为0.1 mm；

其余结构板蜂窝芯子高度Hj：10～60 mm，在其变化范围内取6个平均数，增量为10 mm；

结构板面板厚度Lj：0.2～1.0 mm，在其变化范围内取9个平均数，增量为0.1 mm；

承力筒蜂窝芯子高度Ht：10～60 mm，在其变化范围内取6个平均数，增量为10 mm；

承力筒单层面板厚度Lt：0.01～1.0 mm，在其变化范围内取9个平均数，增量为0.1 mm。

从上述设置的水平数可以看出，蜂窝芯子高度的水平数比其他变量的水平数小，为方便使用正交实验表进行参数组合，采用拟水平法将所有的设计变量的水平数统一为9个。对于蜂窝芯子高度增补的水平数分别是50 mm，40 mm，30 mm。最后参考10个变量，9个水平数的正交设计表，得到如表1所示的参数组合表。挑选出符合实际结构要求与满足强度要求的参数组进行固有频率与质量的计算，为神经网络的训练提供样本。

表1 基于正交实验法的各设计变量的参数组合（部分）

在表1中最后一列“验证”，表示对相应的参数组进行卫星结构的静力计算与校核。Y表示满足结构的强度要求和位移要求，N表示不能满足相应的要求。

通过对表1中满足静力要求的参数组进行卫星固有特性计算，获得相应参数组合的计算结果。为了提高计算效率，本文采用Power dynamics方法进行低阶频率计算（如表2所列）。

表2 各设计变量参数组对应的计算结果（部分）

2.3 神经网络和遗传算法程序编写

在MATLAB7.0软件平台基础上，应用神经网络工具箱中的函数，编写针对已有样本的神经网络程序，并对训练好的神经网络进行样本的检验，直到满足所有检验样本对应的目标值均在许可的范围内为止。

神经网络的结构参数如下：

BP网络，30个隐含层，10个输入变量，2个输出变量；

输入层转移函数为tansig，隐含层转移函数为logsig函数，输出层转移函数采用线性purelin函数，训练函数采用trainlm函数；

初始权系数值由系统的随机函数自动给出，取最大训练步数为5 000步，目标误差精度为1e-4，学习率为0.15；

直到达到训练所要求最大训练步数或目标误差精度为止。

MATLAB7.0中的主程序片段如表3所示。

表3 神经网络主程序片段

在神经网络的训练程序中，将输入输出样本值存储起来，以备后来编写遗传算法程序中所用。神经网络训练过程中，误差的精度和训练步数的关系图见图4。

图4 神经网络训练误差和迭代关系曲线图

从误差曲线看出，训练过程约经过1 300步达到误差精度要求。通过对样本的仿真值的检验，发现训练好的网络泛化能力较强，能够到达预期效果。因此，该神经网络的结构是合理的。

首先根据神经网络的训练结果，在MATLAB7.0软件平台上进行目标函数的多项式拟合。考虑到以一阶频率最大和总质量最小的双目标优化，可以利用加权系数将其转化为单目标优化工作。具体如式（3）。

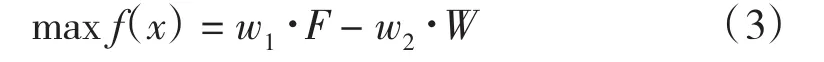
式（3）中，

w1、w2分别为整星结构质量和一阶频率的加权值；

W、F分别为整星结构质量和一阶频率。

根据要求不同，可以设置不同的w1、w2。本章取值：w1=0.4，w2=0.6。

W、F分别除以kg、乘以100/Hz来实现无量纲化。

最终得到以各结构参数为自变量的多项式：

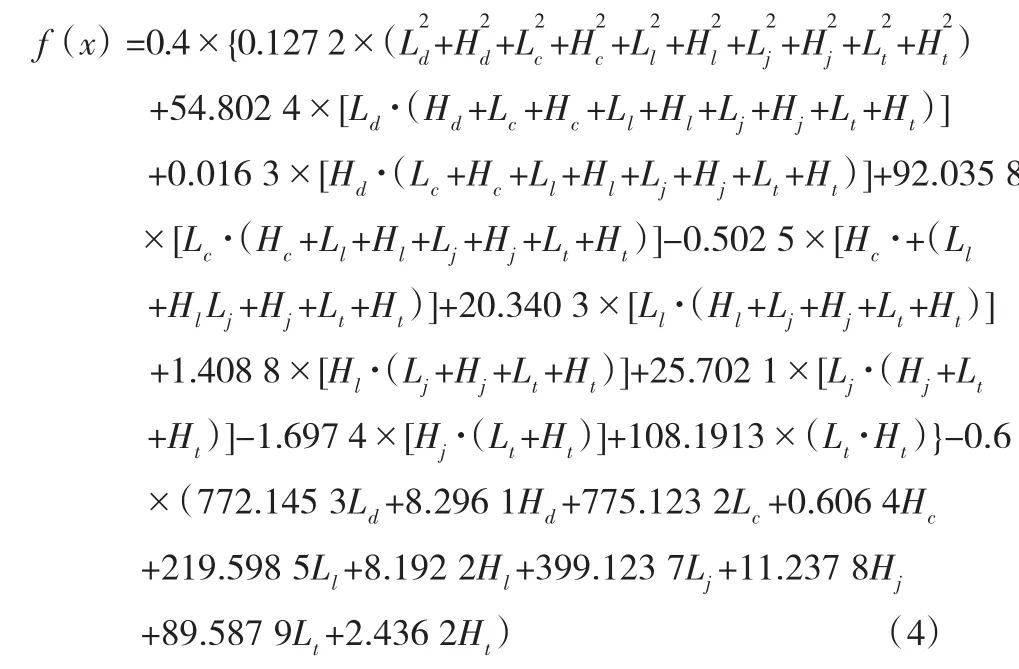
在MATLAB7.0环境下，编制遗传算法主程序及各个相应子程序。设置种群大小为80，交叉概率为0.9，变异概率为0.001，计算代数为200。（见表4）。

表4 遗传算法主程序片段

2.4 优化结果分析

调试并运行程序，得到遗传代数与最佳适应度值变化关系（如图5所示）。

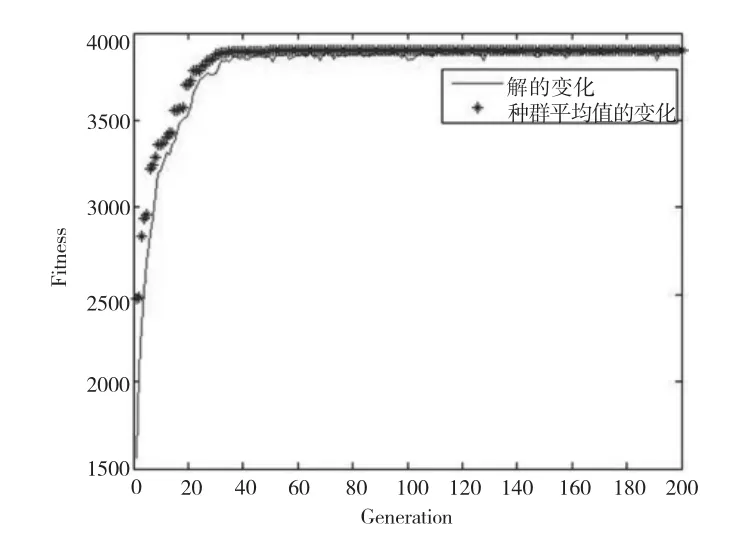
图5 遗传代数与最佳适应度值和平均适应度值的关系

对应的自变量参数值见表5。

表5 优化后得到的设计变量值 （单位：mm）

经过验证，表5所示的参数组满足结构的静力强度要求。对应这组参数的ANSYS计算结果为：一阶固有频率为16.647 Hz，质量为2 314.4 kg。可以认为表5的变量值即为结构设计变量的全局优化值。

使用商业软件ANSYS优化模块，按照传统优化方法的优化结果见表6。

表6 使用传统优化方法的优化结果 （单位：mm）

对应于该参数变量值下的整星结构质量是2306.3 kg，一阶固有频率为14.624 Hz。

比较两种方法的优化结果，使用神经网络结果遗传算法的结构优化设计方法，尽管得到了较大的整星质量，但是在一阶固有频率上有明显的优势。

3 结束语

本文针对卫星结构的多目标优化设计模型，在MATLAB7.0软件平台的基础上，通过BP网络结合遗传算法，完成了一阶固有频率最大、质量最小的多目标优化计算，得到了比较合理的设计变量值。验证了BP网络结合遗传算法在卫星结构优化中的可行性。

笔者将商业软件ANSYS优化模块的优化工作和本文的优化工作对比，得出前者的主要工作是分析文件建立，耗时最多的是迭代过程；后者的主要工作是BP网络的建立和遗传算法的编写，耗时最多的是各正交实验参数下结构计算。在当今MATLAB软件各种工具箱相对完善的情况下，采用后者对复杂结构进行优化计算会更简洁，更省时。

[1]燕乐纬.基于遗传算法的结构动力优化[D].重庆：重庆大学，2006.

[2]吴仕勇.基于数值计算方法的BP神经网络及遗传算法的优化研究[D].昆明：云南师范大学，2006.

[3]Surrry，et al.“A Muti-objective Approach to Constrained Optimization of Gas Supply”[R].Networks.AISBEC,Sheffield,1995.Volume 993/1995,166-180.

[4]Whiltey D.“Modeling Hybrid Genetic Algorithms”[R].In:Genetic Algorithm in Engineering and Computer Science,Winter G(ed).Wiley,1995.

[5]蒋良孝，李超群.基于BP神经网络的函数逼近方法及其MATLAB 实现[J].微机与应用，2004，(1)：52-53.

[6]杨雁宁.利用MATLAB实现BP神经网络的设计[J].河南科技，2005，(8)：46-47.

[7]刘 强，谭光宇，等.基于遗传算法的复杂槽型铣刀片槽型参数优化[J].工具技术，2007，（41）：11-14.