Lotka-Volterra捕食系统的反步控制设计
王晓琴, 马汇海
(1.陕西科技大学理学院, 陕西 西安 710021;2.陕西科技大学电气与信息工程学院, 陕西 西安 710021)
0 引 言
系统的稳定性在生态系统分析中占据十分重要的地位,一个稳定的生态系统对维持其功能是至关重要的.近年来随着工业的发展,生态平衡遭到了严重的破坏.因此,人为地对系统施加有效的控制,使生态系统维持长期平衡是必不可少的[1-4].反步设计法(Backstepping)在工程控制领域得到了广泛重视和实际应用[5,6],实践证明它确实是一种思路清晰、方法简单、效果优良的控制方法,但其用于种群动力学的控制尚不常见,值得进一步研究.
反步设计法又称为反演法,该方法的核心思想是通过逐步修正算法去设计镇定控制器,实现系统的全局调节或跟踪.反步控制的基本设计方法是从一个高阶系统的内核开始(通常是系统输出量满足的动态方程)设计虚拟控制律以保证内核系统某种最为重要的性能,如稳定性、无源性等,然后对得到的虚拟控制律逐步修正算法,但应保持既定性能,进而设计出真正的镇定控制器,实现系统的全局调节或跟踪,使系统达到包含所有期望指标的性能指标.其具体设计步骤如下:
(1)将复杂的高阶非线性系统分解成若干不超过系统阶数的子系统;
(2)给第(1)步得到的每个子系统设计相对独立的部分Lyapunov函数(简称V函数)和中间虚拟控制量;
(3)由系统输出设计一直向后推算,逐渐“后退”到整个系统,将它们集成起来完成整个控制律的设计.
从设计步骤上可以看出,反步法实际上是一种由前向后递推的设计方法,利用一步步的迭代过程去设计新的V函数,最终获得整个系统的稳定性或其他性能.本文通过反步设计法研究了Lotka-Volterra型捕食系统模型的全局稳定性问题,得到了使闭环系统在平衡点处全局渐近稳定的控制规律.
1 Lotka-Volterra捕食者-食饵系统的反步控制设计
1.1 预备知识
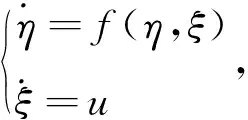
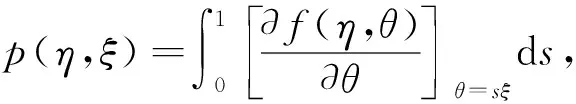
1.2 二维Lotka-Volterra捕食者-食饵系统模型的反步控制设计
在Lotka-Volterra系统中,以二维系统最为简单,但是对它的研究结果对于高维系统而言具有很强的典型性和重要的指导意义,因此人们在研究此类系统时大多是以二维系统为基础而展开的.本节所讨论的对象也正是Lotka-Volterra二维系统中的捕食者-食饵系统,其数学模型表达为:
(1)
式中x1,x2的系数均为常数;a11,a22为种内作用系数,反映两种群的密度作用因素;a12,a21为种间作用系数,反映两种群相互作用的因素;a10,a20表示两种群的内禀增长率,a20>0表示除x1外,x2还有其他食物资源;u是控制量,u的形式将根据反步控制的设计方法给出.
定理:对于系统(1),存在状态反馈控制器
由此可以将式(1)化为对称式
其中aij>0.其反步控制的设计步骤为:
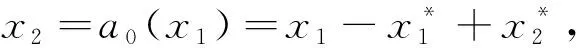
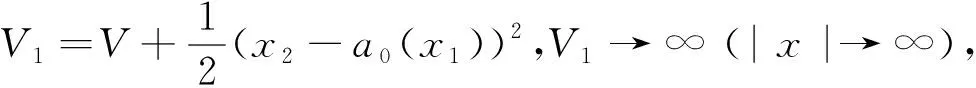
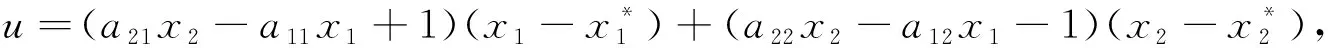
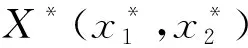
2 实例与数值模拟
2.1 控制规律的设计
考虑如下系统:
(2)
易知u=0时,系统(2)的平衡点(1,2)虽然稳定但非全局渐近稳定.
下面利用反步设计法寻找控制律来达到系统全局渐近稳定.
首先化系统(2)为对称式:
第1步,取V(x1)=x1-1-lnx1,显然V(x1)正定且无界,沿系统有
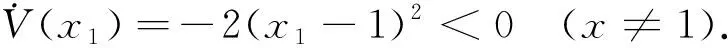
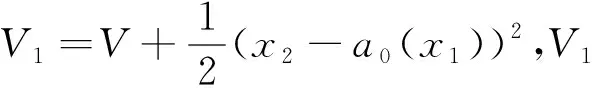
选取
u=(-x2-x1+1)(x1-1)+(x2-x1-1)(x2-2)
(3)
即在反馈控制u下,闭环系统在点(1,2)处是全局渐近稳定的.
2.2 数值模拟
利用mathmatic软件可以分别对无控制规律和以式(3)为控制规律的L-V系统模型进行数值模拟,得到的结果分别如图1和2所示.

图1 原系统的状态曲线 图2 施加控制规律后系统的状态曲线
对比图1和图2可以看出,如果不给系统(2)加以适当的控制,则无论是食饵还是捕食者其种群数量都将会在一定的时间以后逐渐趋于0,这意味着该种群灭亡.而对该系统施加以形如式(3)的人工控制以后,则经过一段时间的发展之后系统会在一定平衡点处趋于某个稳定值,达到了控制目标,其现实意义为无论是捕食者种群还是被捕食者种群都能够维持较长时间的持续共存,从而保证了生态系统的延续性.
3 结束语
本文利用Backstepping反步设计方法研究了二维L-V捕食模型的全局稳定性问题,得到了使闭环系统在正平衡点处全局渐近稳定的控制律.由反步法的设计思想可知,反步设计法使李雅普诺夫函数(V函数)和控制器的设计过程系统化、结构化,因而借助软件编程,整个过程易于实现.由此可见,本文的研究有一定的理论和应用价值.此外,反步法中引进的虚拟控制本质上是一种静态补偿,前面的子系统必须通过后面子系统的虚拟控制才能达到镇定的目的,因此要求系统结构必须是严参数反馈系统或可经变换化为该种类型的非线性系统,这样也使反步法的应用受到了一定的限制.
参考文献
[1] 陈兰荪,宋新宇,陆征一.数学生态学模型与研究方法[M].成都:四川科学技术出版社,2003:1-180.
[2] 赵立纯.种群动力学系统控制问题的研究[D].沈阳:东北大学硕士学位论文,2003.
[3] 田亚品,陈斯养.N-种群Lotka-Volterra扩散竞争反馈控制生态系统的持久性和全局渐近性[J].应用数学,2007,20(3):485-490.
[4] 郑秀亮,唐妍霞.N+M维Lotka-Volterra捕食-竞争时滞系统的渐近性[J].安徽大学学报(自然科学版),2011,35(6):24-29.
[5] 程代展,洪奕光,秦化淑.多输入非线性系统后推(Backstepping)型[J].控制理论与应用,1998,15(6):824-830.
[6] Li J,Xu D M,Ren Z.Backstepping Variable Structure Control of Nonlinear Systems with Unmatched Uncertainties[C].Proc.of the 14th IFAC World Congress,Beijing,PRC,1999:67-71.
[7] A.Isidori.Nonlinear Control Systems[M].3rd.ed.Berlin:Springer-Verlag,1995.

