斜拉桥健康监测信号改进小波相关降噪❋
严 鹏, 李 乔, 单德山
(西南交通大学土木工程学院 成都,610031)
引 言
在建立桥梁结构健康监测系统后,需要对系统采样信号进行分析,以评价结构状态和识别结构损伤。桥梁结构通常处在复杂的外界环境中,在各种因素的影响下,桥梁健康监测系统输出信号总是受到噪声的干扰,结构的大量有用信号淹没在噪声之中,导致损伤识别率偏低。因此,在信号分析过程中,首先必须对系统输出信号进行降噪处理,最大限度地消除噪声的影响,对准确评价结构状态和识别结构损伤具有重要意义。
目前,国内外不少学者对降噪方法进行了研究,小波降噪是其中较常用到的方法。小波降噪方法主要有3类,即小波阈值降噪[1]、小波模极大值降噪[2]和小波相关降噪[3]。其中小波相关降噪充分利用了信号和噪声在小波分解各层相应位置上不同的相关性特点[4],算法易于实现,降噪效果较好。文献 [5]介绍了一种传统小波相关降噪算法。文献[6]对传统算法进行了改进,并通过数值试验证明该方法具有更好的去噪效果。
在上述小波相关降噪的文献中,相邻小波系数相关检测范围的确定没有考虑小波各尺度系数的特征。将小波系数的绝对值或能量作为降噪阈值也不准确,导致小波系数幅值较小的有用信号误判为噪声而被滤除。在进行信号重构时,均采用传统算法,忽视了除最后一层外所有尺度的低频系数相关检测阈值处理结果,使得重构信号中缺少足够的趋势信息。为此,笔者针对传统小波相关降噪算法的缺陷,基于斜拉桥健康监测信号特征,提出一种改进的小波相关降噪算法,对斜拉桥健康监测动态信号的降噪处理进行研究。
1 改进小波相关降噪算法
1.1 改进措施
1.1.1 相关检测邻域范围改进
相关检测邻域范围必须有合适的大小。桥梁响应信号的整体信息由周期信号体现,而细节信息则由突变信号体现。反映信号整体特征,需要相关检测邻域范围足够大,能够将周期信号包含在内;而反映信号细节特征,则需要相关检测邻域范围尽量小,以突出突变信号的局部特征。因此,在确定相关检测邻域范围时,需要做到两者之间的平衡。
小波变换将斜拉桥动态响应信号各阶主要能量周期分解到不同尺度的小波系数中,采用主要能量周期为各层相关检测邻域范围,在确保能将信号主要整体特征包含在内的前提下,以最小范围反映了信号局部特征。各层相关检测邻域范围随着该层系数的主要能量周期自适应地变化,使求得的相关量能够较为完整、无冗余地反映相邻系数的局部相似程度。
1.1.2 降噪阈值改进
Bruce等[7]证明了硬阈值法有较大的方差,而软阈值法有较大的偏差,信号重构的准确性比精密性更为重要,选用硬阈值法进行降噪。为了避免传统算法中低幅值信号误判为噪声而滤除的情况发生,规定降噪阈值为某一固定值。当局部相关系数大于该阈值时,保留此范围小波单支重构系数,反之则置零。
1.1.3 信号重构计算改进
根据小波分解的 Mallat算法,重构信号可以表示为各单支重构系数之和[8]。据此提出一种全新的信号重构算法,该算法推导过程为

等式左右同时求和,得

其中:S为重构信号;A为小波分解低频系数的单支重构系数;D为小波分解高频系数的单支重构系数;L为小波分解层数;P为临时向量。
按式(3)重构信号,在计算中充分利用了所有尺度的低频系数,使得重构的信号保留了足够的经过阈值处理的趋势信息。
1.2 改进步骤
改进小波相关降噪算法具体步骤如下:
1)小波变换。确定小波基和小波分解层数,进行监测信号二进小波变换;
2)小波系数单支重构。为了便于相关检测,进行各层小波系数单支重构,使相邻各层系数长度相同;
3)计算各层单支重构信号的自相关函数,求出其频谱。采用峰值法求得各层信号的主要能量周期Tj,j为分解层数,以该周期作为之后相关检测的邻域范围值;
4)信号延拓。对所有各层单支重构信号进行延拓,采用反对称延拓模式,向两个方向各延拓信号原长度的 1/4;

5)计算延拓后相邻小波单支重构系数Yj和Yj+1的局部相关量其中:j为尺度;m为相关检测邻域的中心值;n为相关检测邻域的大小,即等于各层主要能量周期值Tj;其中j的最大值为L-1,L为小波分解层数。
相关量计算从延拓前信号的初始位置开始,并将求得的相关系数赋给以m为中心、n/2范围大小邻域组成的分段叠加相关系数

6)循环移动相关检测。重复步骤5,每次正向移动n/2,直至m移动到延拓前信号的结束位置;
7)阈值处理。将分段叠加相关系数的绝对值与固定阈值进行比较,如果前者较大,则保留分支重构系数的值,反之则置零;
8)求出降噪信号。对阈值处理后的各层分支重构系数按式(3)计算,得到降噪信号。
改进小波相关降噪算法流程如图1所示。
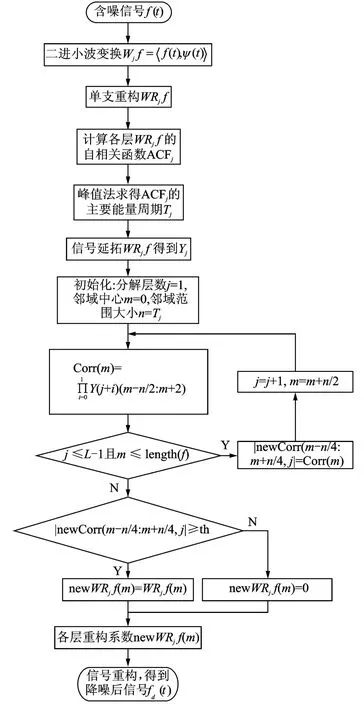
图1 改进小波相关降噪算法流程图
2 降噪评价指标
在进行信号降噪研究时,无噪信号是已知的,可以采用信噪比改善比(SNRI)作为评价各种条件下不同算法的降噪效果指标。 SNRI是降噪后与降噪前含噪信号的信噪比相对增量,其值越大,降噪效果越好。 SNRI定义为

其中:SNRin为降噪前信号的信噪比;SNRout为降噪后信号的信噪比。
其中信噪比 SNR计算公式为

其中:s(n)为含噪信号;(n)为无噪信号;N为信号采样数量;SNR的单位为dB。
3 仿真试验
3.1 仿真试验信号
斜拉桥主梁结构振动频率较低,通常在[0.15,2]Hz内[9-10]。考虑到结构响应的频谱为多极值曲线,极值即对应各阶频率,可以将数值仿真信号简化为极值对应频率在该范围内的信号。
根据桥梁健康监测动态信号特征,选取 3种典型信号作为数值仿真信号,以验证提出的改进小波相关降噪算法的适用性和有效性。这 3种数值仿真信号分别为单频率正弦信号、单频率正弦+脉冲信号和双频率正弦信号,分别用于模拟单自由度结构响应、受冲击荷载的单自由度结构响应以及两自由度结构响应。各种信号添加高斯白噪声,然后对不同频率和信噪比的含噪信号进行降噪处理。数值仿真信号特征见表 1。

表1 数值仿真信号
为了验证实际斜拉桥结构响应的降噪效果,采用 ANSYS建立桥梁结构有限元模型,进行有限元仿真信号降噪处理研究。模型以如图 2所示某大型桁架斜拉桥为依据,其主桥为双塔双索面斜拉桥,跨度布置为(81.9+ 135+432+ 135+ 81.9)m,总长865.8 m。

图2 某大型斜拉桥总体布置 (单位:m)
模拟桥址所在位置的环境振动,对有限元模型施加均值为 0、标准差为 0.1 m/s2的高斯白噪声激励,进行瞬态分析,提取主梁跨中正中结点的竖向位移响应进行处理,响应时长为20.48 s。根据模态分析可知,该桥前 10阶振型的频率范围为 0.184~1.010 1 Hz,其位移响应的主要频率也在此范围。进行降噪处理研究时,在位移响应中添加高斯白噪声,为便于对比,信噪比 SNR的取值与前述数值仿真信号相同。
在仿真信号的改进小波相关降噪处理的同时,进行传统小波相关降噪(小波系数相关检测邻域范围固定为含噪信号主要能量周期)和小波默认阈值降噪[11]的对比。在降噪计算时,参照常用小波基参数[12],小波基采用 bior3.1,分解层数定为 5层。
3.2 降噪阈值确定
降噪阈值的准确确定是提出的改进算法能够有效降噪的关键。根据斜拉桥有限元仿真结果,可以归纳出最佳降噪阈值。当信噪比分别为13,10,7,4和3 dB时,降噪后信号的 SNRI值随降噪阈值的变化如图 3所示。

图3 SNRI随降噪阈值变化
由图3可见,在含噪信号的各信噪比条件下,降噪后信号的 SNRI值均在降噪阈值为 0.7时达到最大。因此,对于斜拉桥健康监测动态响应信号降噪来说,降噪阈值可以取为 0.7。
值得注意的是,该降噪阈值是通过试算确定的。由于桥梁结构种类繁多,体型各异,其响应并没有统一的信号特征,无法采用相同的阈值进行降噪处理,因此在实际工程应用中,可以采用上述方法,通过有限元建模计算完成降噪阈值的选择。
3.3 各层局部相关系数
小波单支重构系数局部相关的阈值降噪是本文算法的核心内容。以斜拉桥有限元仿真结果为例,对相邻各层小波单支重构系数进行局部相关检测,得到的各层相关系数如图4所示。图中A1和A2表示小波单支重构系数A1和A2的局部互相关系数,其他名称以此类推。其中:A表示小波分解的低频部分;D表示小波分解的高频部分。
图4(c~ j)的横坐标为采样点数,纵坐标为相关系数值。图中实线为相邻各层的局部相关系数,各实线为分段直线,而分段长度就是其局部相关检测的邻域范围;水平点线为降噪阈值,这里均为0.7。当局部相关系数值大于降噪阈值时,认为该段小波单支重构系数为信号而保留;反之认为是噪声而去除。
由图 4可见,大部分低频系数相邻各层的局部相似性均较阈值高,这部分系数作为有用信号而保留;大部分高频系数相邻各层的局部相似性则较阈值低,仅有少数系数值大于阈值,这部分较大的系数作为原始信号中的突变信号而保留。

图4 相邻各层小波单支重构系数局部相关系数
从相关检测邻域范围的分析可知,邻域范围过小或过大均会导致相关系数值减小,这样低频成分的部分有用信号和高频成分的部分噪声将会被误判,从而降低降噪效果。因此,以各层主要能量周期作为相关检测邻域范围,能够最大程度地实现信噪分离。
此外,小波低频系数的相关检测邻域范围较大,适合用于周期信号的识别;而高频系数的邻域范围则较小,随着阶数降低而减小,适合突变信号的识别。这种变化进一步充分证实了该方法相关检测邻域范围变化的自适应性。
3.4 降噪效果随频率的变化
信号频率的改变将导致不同算法降噪效果的差异,特定的降噪算法只能适用于某一频率区间,对于该区间之外的频率,其降噪效果则急剧下降。在验证降噪算法效果时,根据斜拉桥健康监测动态信号的频率范围,近似等间隔地选取频率为 0.15,0.5,1,1.5和 2 Hz的仿真信号作为研究对象,添加相同信噪比的高斯白噪声并进行不同算法的降噪处理。
图5为 SNR=7 dB时,3种类型数值仿真含噪信号的 SNRI随信号频率的变化情况。
在 3种降噪算法中,改进小波相关降噪显示了独特的优势,其 SNRI值不仅在不同频段皆大于零,而且数值较大;传统小波相关降噪由于其固有缺陷,降噪效果最差,反而致使信噪比下降;小波默认阈值降噪则不适用于斜拉桥健康监测信号频段,当频率较高时SNRI值小于零。因此,改进小波相关降噪算法更适用于斜拉桥健康监测动态响应信号降噪。
不管哪种类型的信号,经改进小波相关降噪后,其 SNRI值均随频率增加而下降。噪声通常处于较高的频段,随着无噪信号频率的增加,两者在频域上逐渐难以区分,因此,SNRI值将随着信号频率的增加而降低。
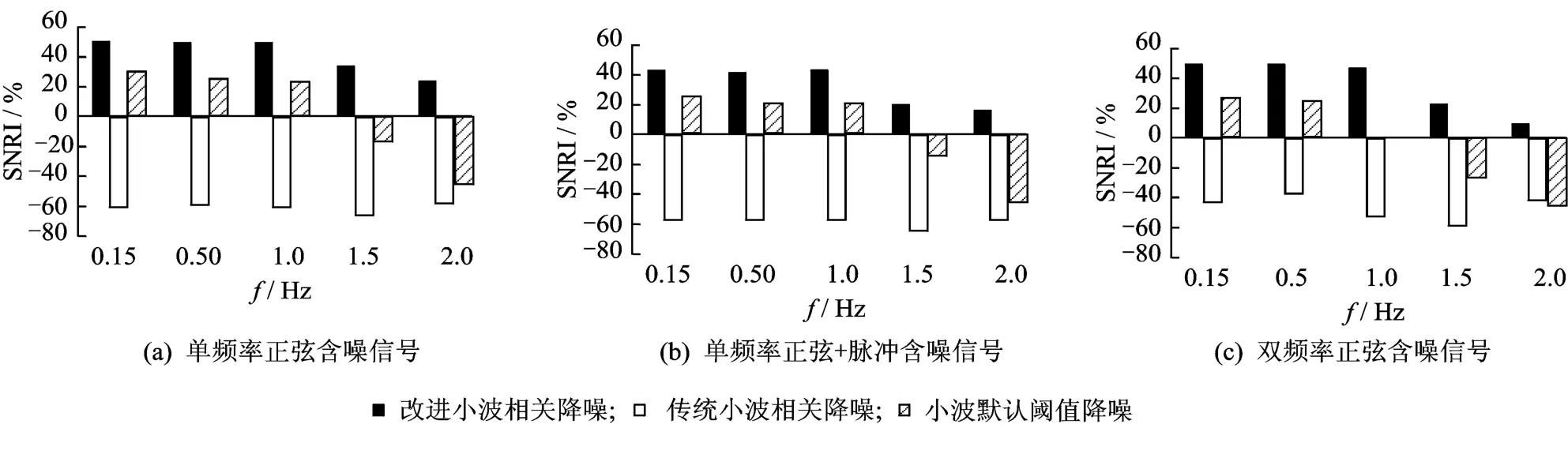
图5 SNRI随信号频率的变化
3.5 降噪效果随信噪比的变化
SNR的大小将直接影响含噪信号与无噪信号的差异,信噪比越小则所含噪声比例越大,越难以将原信号从含噪信号中分离出来。一种好的降噪算法能够适应不同的信噪比,为了验证各种降噪算法的有效性,对一组固定频率的信号进行研究,其 SNR分别为 13,10,7,4和 3 dB,采用不同算法对其进行降噪处理研究。
图6为 3种类型数值仿真含噪信号(频率f=1 Hz)和有限元模型位移响应含噪信号的 SNRI随信噪比的变化情况。
在 3种降噪算法中,改进小波相关降噪算法的效果尤为明显,其 SNRI值均大于零,数值相对较大,不同信号类型也都有较好的数值稳定性;传统小波相关降噪算法由于其固有缺陷,降噪效果最差,处理后的信号信噪比反而降低;小波默认阈值降噪算法的降噪效果处于两者之间,在某些信噪比条件下其SNRI值小于零。因此,改进小波相关降噪算法更适用于斜拉桥健康监测动态响应信号处理。
图7为各种算法对有限元模型位移响应含噪信号降噪结果对比,图中含噪信号信噪比SNR=7 dB。由图可以直观看出,改进小波相关降噪算法的降噪结果较好,不仅体现了无噪信号的总体趋势,也较大程度保留了其突变细节部分,具有另外两种降噪算法不可比拟的重构无噪信号的优势。因此,改进小波相关降噪算法更适用于斜拉桥健康监测的动态响应信号降噪。

图6 SNRI随信号 SNR的变化
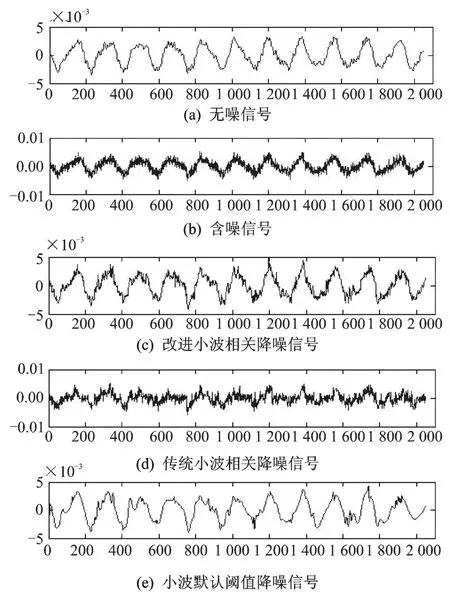
图7 动态位移响应信号降噪结果
4 结 论
1)针对斜拉桥动态响应信号特征,依据小波单支重构系数的主要能量周期,创造性地提出了小波相关降噪算法中相关检测邻域范围的自适应确定算法。该算法能够最大限度地反映相邻系数的局部相似程度,使小波相关降噪达到最佳效果。
2)重新确定新的降噪阈值,避免传统算法中较小幅值信号被误作噪声滤除的现象发生。该降噪阈值是通过试算产生的,对同类型斜拉桥健康监测动态响应信号的降噪计算具有参考意义。其他类型的桥梁可以参照该方法,得到相应的降噪阈值。
3)提出一种全新的信号重构算法。该算法在计算中充分利用了所有尺度的低频系数,使得重构的信号保留了足够的经过阈值处理的趋势信息,最后采用平均处理得到降噪信号。
4)改进的小波相关降噪算法仅对斜拉桥动态响应频率范围内信号的白噪声去除有较好的效果。
[1] Donoho D L,Johnstone I M.Ideal spatial adaptation via wavelet shrinkage[J].Biomefrika,1994,81:425-455.
[2] Mallat S,Hwang W L. Singularity detection and processing with wavelets[J]. IEEE Trans Inform Theory,1992,38(2):617-643.
[3] Xu Y,Weaver J B,Healy D M,et al.Wavelet transform domain filters: a spatially selective noise filtration technique[J].IEEE Trans Image Processing,1994,3(6):747-758.
[4] 周美玲.基于二进小波相关系数的比例萎缩图像去噪 [D].曲阜:曲阜师范大学,2007.
[5] 成礼智,王红霞,罗永.小波的理论与应用 [M].北京:科学出版社,2004:283-284.
[6] 向东阳,吴正国,胡文彪,等.改进的小波变换系数相关去噪方法[J].振动、测试与诊断,2010,30(5):561-565.
Xiang Dongyang,Wu Zhenguo,Hu Wenbiao,et al.Improved denoising algorithm using correction of wavelet coefficient[J]. Journal of Vibration,Measurement&Diagnosis,2010,30(5):561-565.(in Chinese)
[7] Bruce A G,Gao Hongye.Understanding w ave shrink:variance and bias estimation[J].Biometrika,1996,83(4):727-745.
[8] 杨福生.小波变换的工程分析与应用 [M].北京:科学出版社,1999:64-68.
[9] 樊可清,倪一清,高赞明.大跨度桥梁模态频率识别中的温度影响研究[J].中国公路学报,2006,19(2):67-73.
Fan Keqing,NiYiqing GaoZanming. Research on temperuture influences in long-span bridge eigen frequencies identificaton[J].China Journal of High Way and Transport,206,19(2):67-73.(in Chinese)
[10]车树汶,陈权,楼松庆.质量矩阵模式对桥梁自振频率的影响 [J].兰州铁道学院学报:自然科学版,2003,22(6):80-83.Chen Shuwen,Chen Quan,Lou Songqing.Influence of mass matrix model on natural vibration frequency of bridges[J]. Journal of Lanzhou Railway University:Edition of Natural Science,2003,22(6):80-83.(in Chinese)
[11]胡昌华,李国华,刘涛,等.基于 M ATLAB 6.x的系统分析与设计——小波分析[M].3版.西安:西安电子科技大学出版社,2004:292-301.
[12]Daubechies I.Ten lectures on w avelets[M].Philadephia:Society for Insductrial and Mathematics,1994:194-202.

