经验模态分解滤波器组特性及轴承异音识别❋
黄迪山,刘玉霞
(上海大学机电工程及自动化学院 上海,200072)
引 言
Huang在 1998年提出了一种全新的信号时频分析方法-HHT,该方法的核心内容是经验模态分解(EMD),即把信号分解成多个相互正交本征模态函数(imf)[1]。 EMD分解具有自适应滤波性质,文献[2-3]对 EMD滤波器组特性进行研究,通过 5 000次独立的高斯噪声进行 EMD分解,分别得到imf的频谱。经过观测和分析推知,当输入信号为高斯噪声或具有广谱性时,EMD具有和二进离散小波分解完全类似的二进滤波器组结构的特性。本文在高斯噪声 EMD分解中,改变判别参数 SD,研究EMD滤波器组特性。通过大量独立的数值计算,发现 EMD滤波器组特性是可调整的,文献 [2-3]中所观测到的二进制小波特性是一种特殊条件下的现象。EMD滤波器组特性的可调整性将为EMD分解信号分析拓宽应用前景。
轴承异音指轴承运转过程中,除了均匀的基音以外,还伴随周期性和随机性的各种声音[4],它的频谱具有广谱性。因此,根据轴承振动加速度的广谱性,文中将 EMD对轴承振动加速度信号进行分解,利用参数 SD对 EMD滤波器组特性的可调性,实现振动信号按异音测量要求进行自动频段分离。结合前三阶本征模态的 ST FT处理,实现轴承异音在时频域上的识别。
1 高斯随机噪声经验模态分解
假设n(t)为高斯随机噪声信号;imfi(t)为EMD分解得到的本征模态函数,r(t)为余量,则高斯噪声信号可以表达为所有的imfi(t)及余量r(t)
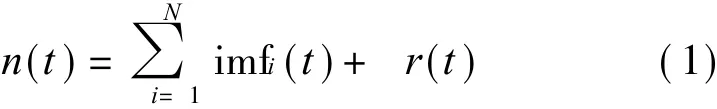
在 EMD分解中,采用递推过程实现高斯噪声信号“筛”过程的数值计算。考虑到较少递推次数和较小的包络平均计算误差,用统计参数SD控制“筛”过程的次数

文献 [1]对 1 024点数据进行 EMD分解,推荐SD=0.2~ 0.3为“筛”过程的递推停止判据,相当于递推次数 4~10的情况。在这种条件下,对高斯噪声信号进行 EMD分解,滤波器组特性表现为二进制小波特性,即相邻滤波带的中心频率之比为

但是在式(2)中,会遇到某些点h1,k-1(t)=0情况,对不利于SD数值计算。为此笔者采用的递推停止判据为
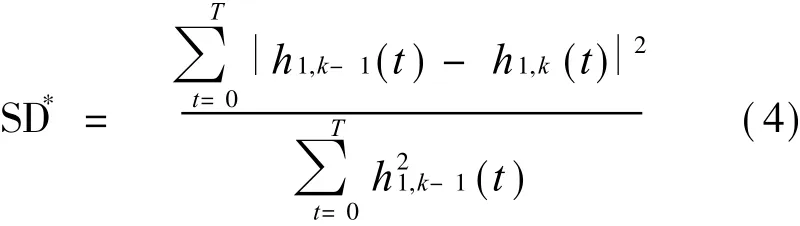
在EMD分解中,如果改变判据参数SD*取值范围,不仅影响 EMD分解中递推次数,而且 EMD滤波器组特性将随之改变。
在数值试验中,对 1 024点高斯随机噪声信号n(t)进行5 000次独立 EMD分解,采用三次样条插值EMD算法,其中取循环停止判据参数SD*=0.3,0.03和 0.003,取前 7个本征模态信号 imf1~ imf7。为了防止分解过程中的端点误差进入本征模态信号imfi(t)的频谱,除了作端点处理外,从本征模态信号imfi(t)的中间取8 192点进行傅里叶变换,得到相应的归一化频谱,最终将各个imfi(t)的频谱汇总在同一图上(见图 1)。
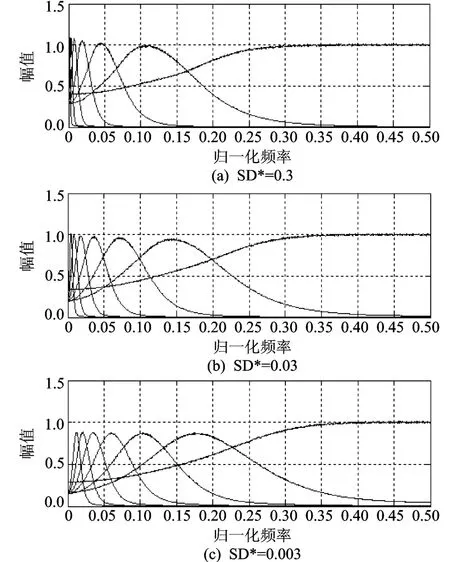
图1 3种判据 SD*的高斯噪声经验模态分解结果
反复数值试验结果显示,不同的判据参数 SD*取值,得到不同的 EMD滤波器组特性。最明显的特征是 EMD滤波器组的中心频率变化:
1)当判据参数 SD*减小时,在高斯随机噪声信号进行 EMD分解中,滤波器组的中心频率右移;反之,则中心频率左移。
2)当判据参数 SD*变化时,相邻滤波带的中心频率之比随之改变,具体的数据见表1。当判据参数SD*取值为 0.03,对高斯噪声信号进行 EMD分解,滤波器组呈现二进制小波特性。如果判据参数 SD*偏离 0.03时,滤波器组将不再保持二进制小波特性,即相邻滤波带的中心频率之比


表1 相邻滤波组中心频率之比与判据参数SD*关系
通过改变判据参数 SD*,能在一定范围内改变滤波器组的特性,但判据参数 SD*的大小影响 EMD分解的计算速度。
2 轴承异音检测应用
应用 EMD分解对轴承振动加速度信号进行分解,实现自动频段分组。对轴承异音,由数值试验方法,确定递推判据SD*=0.3,实现EMD分解中滤波器组的中心频率调整。
在试验研究中,选用异音强度中等偏下(人耳判别)的 608系列深沟球轴承,在安德鲁轴承试验机上进行驱动,转速为 1 800 r/min,外圈固定并且轴向加载 2.25 kg,进行振动测试。用传感器B&K 4517-002拾取轴承振动加速度,用 PULSE分析仪 3560-B-120对振动信号采集,得到如图 2(a)所示的 0~12.8 kHz轴承振动加速度信号。
图2(b~f)是轴承振动加速度信号由EMD分解后的本征模态函数(imf1~imf5)。本征模态信号imf1,imf2,imf3可显示轴承瞬间的高、中、低频段振动加速度信号,反映了轴承的异音成分。
3 轴承异音的通频段识别
对轴承振动加速度信号的 EMD分解的前 3个本征模态信号 imf1,imf2和imf3之和进行短时傅里叶变换,得到时频的三维表达,即轴承加速度信号的时间、频率和幅值分布。通过对三维图的特征识别,实现对轴承异音在通频段的判别。
图3(a)是图 2中(b,c,d)本征模态信号之和的时频分析,给出了异音发生时通频段的三维表示。在0~ 5 m/s2幅值范围作均匀 20等份等高线,得到图 3(b)所示的等高线投影,给出时频分析的等高线表达。
无论从三维时频图还是从两维时频等高线图,都可以观测到轴承异音在低频段分布着幅值较大的冲击信号,并且带有周期性。在中频段则分布着周期性不明显而幅值相对较小的冲击信号;在高频段则密布着微小的随机性冲击信号。
4 异音分级判定

图2 轴承振动加速度信号及其本征模态函数(imf1~imf5)
轴承异音是幅值大小不等、频率不等、周期和随机性的冲击,其时频特征形式繁多。图4列举了典型轴承异音信号,其特性明显不同于图3情况。其中图4(a)是异音强度中等偏下情况,异音的频率主要分布在中频段,并且振动延伸到高频段;图4(b)则是一个无异音情况,只有微小冲击分布在两个共振带上。由于振动幅值太小,时频域的等高线图案不再出现。
根据多个异音强度中等偏下的轴承测定,结合振动加速度信号的 EMD分解和时频分析,异音的确定可以从时频域的峰值或有效值判定。峰值判定对轴承具有周期性冲击的情况非常有效,如图 3(a)和图4(a)。从峰值大小可以确定异音存在。虽然从三维图可直接观测,但不够精确。设置等高线的密度,使等高线与阈值有关,这样从等高线直接可以判定异音存在、及轴承的异音分级。当最低的等高线设为阈值(例中为 0.5 m/s2)时,如果异音存在,等高线图就会呈现;否则如图 4(b)无异音情况,不存在等高线,图中出现一片空白。
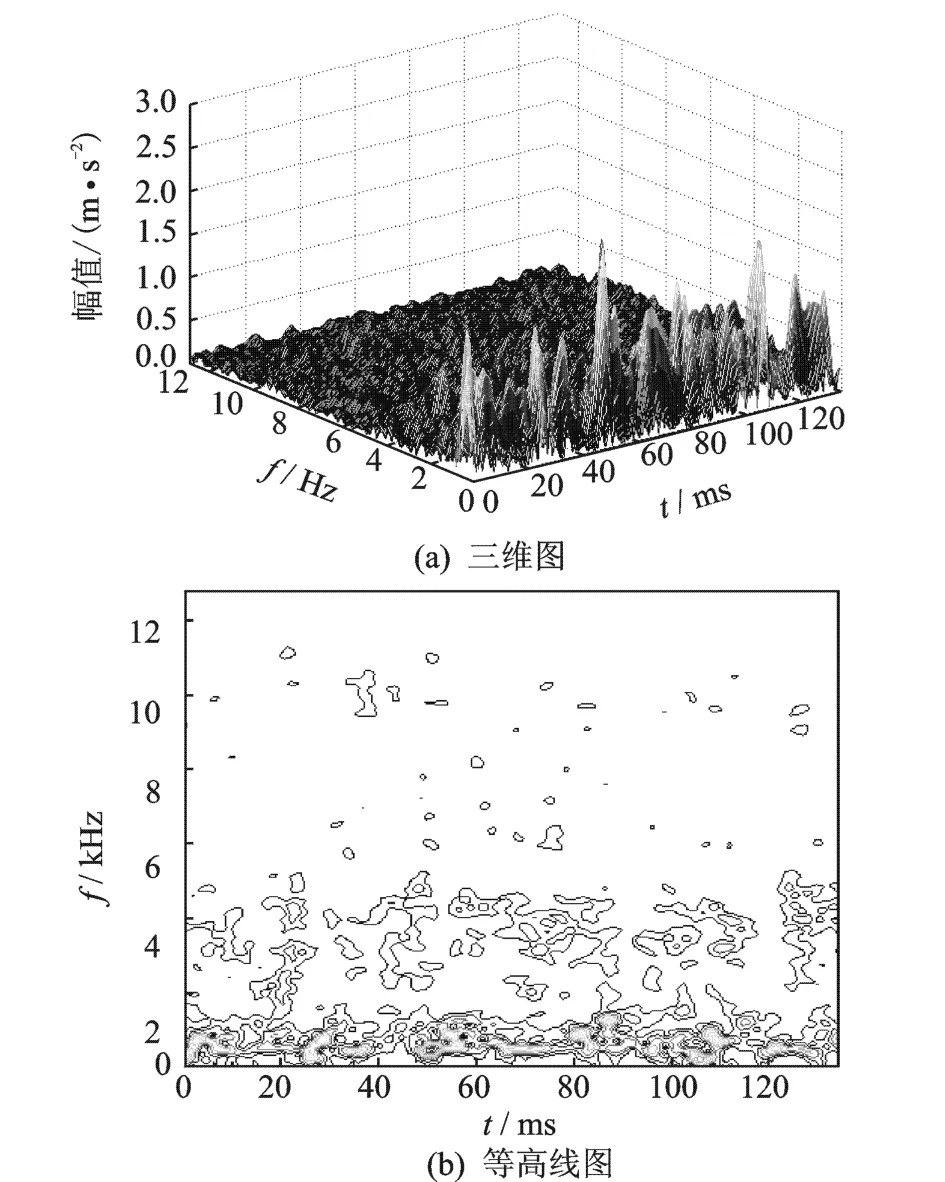
图3 轴承异音的时频域表示
有效值则可统计随机分布为主导的冲击能量,如图 4(c)情况,通过有效值计算可判定异音存在。
5 轴承异音的低、中、高频段识别
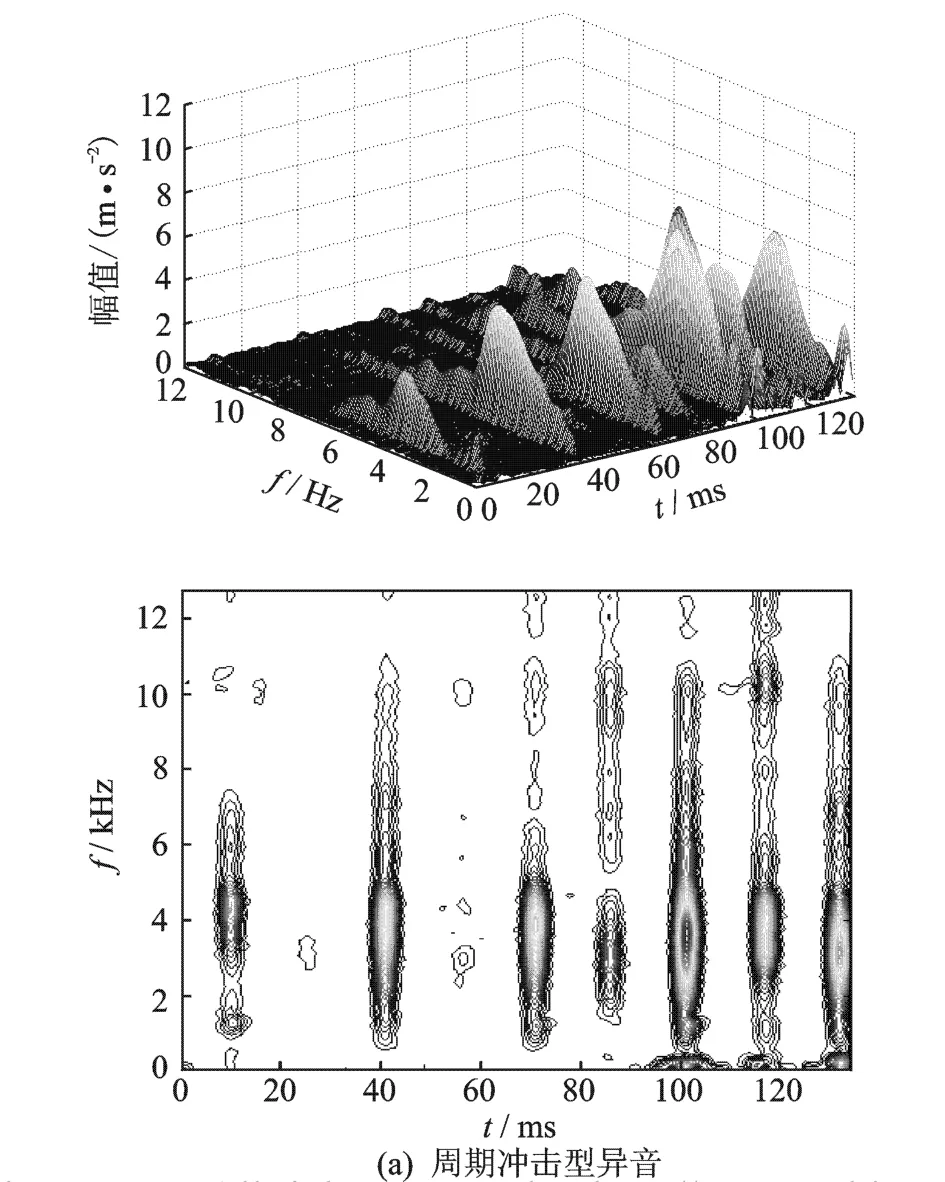

图4 608系列深沟球轴承异音分析
对轴承振动 EMD分解的各阶本征模态信号分别进行 STFT处理,实现对轴承的高、中、低频段异音识别。对图4(a)情况作分段 ST FT处理,如图 5所示。图5(a)表明轴承高频段异音情况,图5(b)表明轴承中频段异音情况,图 5(c)表明则轴承低频段异音情况。
由于不同频段可采用不同尺度的高斯窗进行ST FT处理,在高频段时频分析中冲击的时间分辨率得到提高。
6 异音模式识别
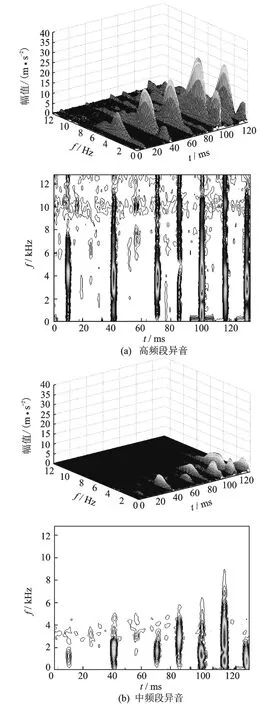
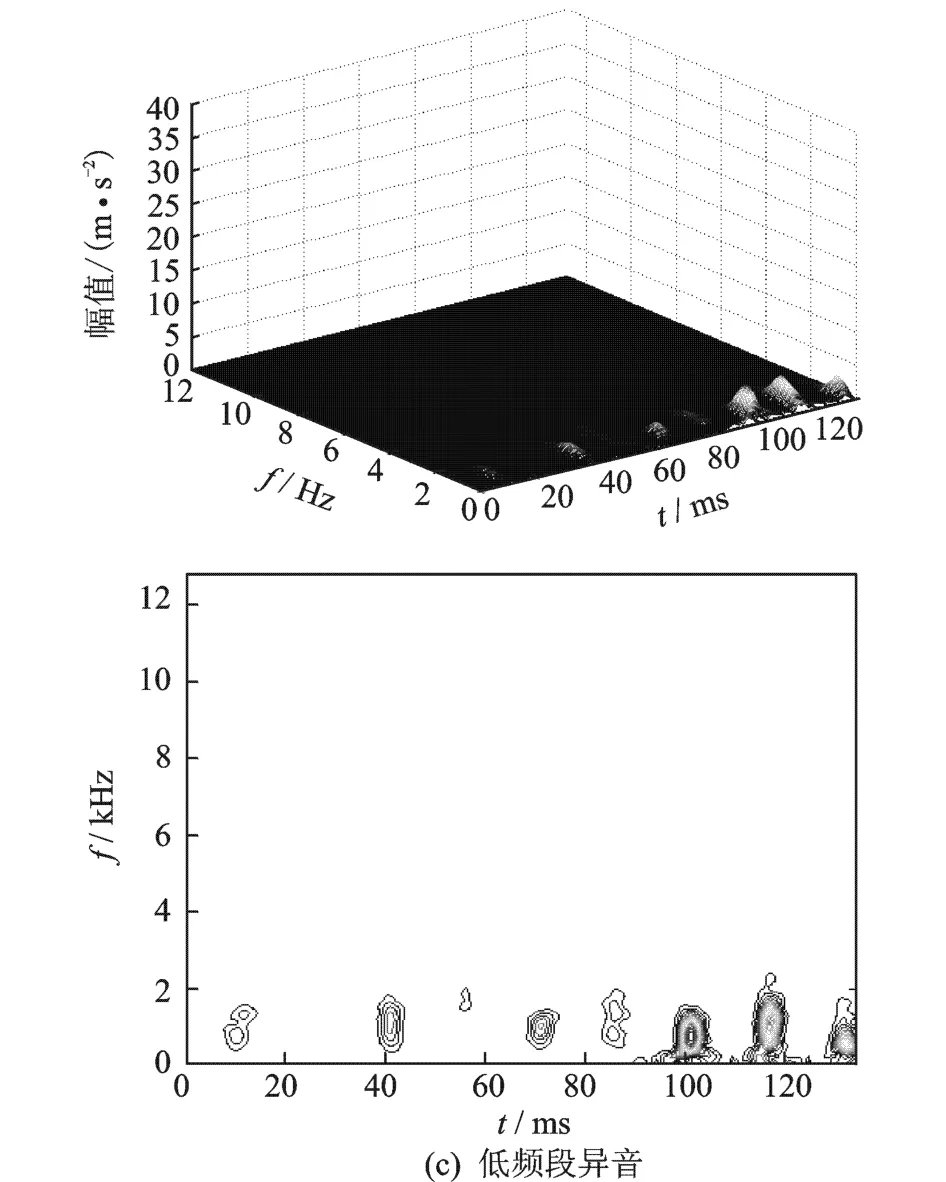
图5 轴承异音的低、中、高频段识别
应用EMD和STFT不仅对轴承异音实现分级,而且从三维刻画的分布识别轴承异音的类别,跟踪轴承质量有关的加工过程。文中已列举了一些典型轴承异音情况。在图 3中,振动在低频段呈周期性,异音的出现与轴承内外滚道圆形偏差有关;在图 4(a)中,振动高频冲击,有周期性,异音的出现与轴承滚道的局部缺陷对应;在图 4(b)中,在三维图上没有显示大的冲击,但明显存在两条低幅度的共振带,有窄带随机分布特征,是有轴承表面正常粗糙度对轴承滚道激励形成的,这种轴承加工质量上乘,异音小;图4(c)则在三维图上振动幅度较大并呈窄带随机分布,这是轴承滚道粗糙度过大引起的。三维图分布提供各种轴承加工质量的异音模式,可以帮助识别轴承加工质量误差源。
7 结 论
1)在高斯噪声 EMD分解中,采用三次样条插值算法,通过调整参数 SD*,改变了 EMD滤波器组特性。
2)利用参数 SD对滤波器组特性可调性,实现轴承振动信号按异音测量要求进行自动频段分离。对前 3阶本征模态函数进行短时 STFT处理,把轴承异音的幅值大小、频率大小、周期和随机分布冲击特性在三维图中刻画出来。
3)通过对 ST FT幅值和有效值的阈值设定,能客观地判定轴承各种异音存在。通过三维分布表达,能有效识别轴承异音模式,分析生产过程中加工质量误差源。该信号处理方法直观、易懂,可用于超静音轴承制造中的异音品质控制。
[1] Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceeding of the Royal Society A,1998(454): 903-995.
[2] Flandrin P,Rilling G,Goncalves P.Empirical mode decomposotion as a filterbank[J]. IEEE Signal Processing Letter,2004,11:112-114.
[3] Chen Qiuhui,Huang N E,Sheman D,et al.A B-spline approach forempirical mode decompositions[J].Advance in Computation Mathematics,2006,24:171-195.
[4] 邱明,李济顺,张洛平,等.深沟球轴承异常声评定指标的探讨[J].轴承,2002,3:26-29.
Qiu Ming,Li Jishun,Zhang Luoping,et al.Discussion on evaluation for a abnormal vibration of deep groove ball bearing[J].Bearing,2002(3):26-29.(in Chinese)

