高速铁道车辆天棚阻尼悬挂系统时滞稳定性分析

廖英英， 刘永强， 杨绍普， 魏红梅

(1．石家庄铁道大学 土木工程学院，河北 石家庄 050043;2．石家庄铁道大学 机械工程学院，河北 石家庄 050043;3．山东华宇职业技术学院，山东 德州 253034)

0 引言

我国铁路第六次大提速以后，干线客运列车的运营速度可以达到200 km/h，高速客运专线运营速度超过300 km/h，为人们的日常出行和经济提升提供了坚实的保障。但随着运行速度的提高，车辆振动加剧，对铁道车辆的运动稳定性、运行平稳性和安全性等产生了严重影响。半主动控制技术的提出为解决这一难题提供了思路，国内外的众多专家学者在理论上对半主动控制效果进行了分析［1-3］，结果表明:相对于被动控制，半主动控制技术可以提高铁道车辆运行平稳性20%以上。然而，在实际运用中半主动控制效果却远远低于这一数值［4］。究其原因，控制系统中存在的时滞是造成半主动控制效果差的重要因素之一。

时滞是指在控制系统的信号采集、传输，控制器规则形成和作动器输出等过程中存在的时间滞后现象，最终表现为在系统不需要能量时作动器输出能量，这就会造成控制效果变差和系统特性的改变，甚至会造成系统失稳等。国内外学者对悬挂系统中时滞造成的稳定性问题进行了大量的研究。胡海岩和王在华［5-6］曾对带时滞的天棚阻尼主动悬架和考虑司机反应时滞的四轮驱动车辆系统的稳定性转换问题进行研究。张文丰［7］，翁建生［8］和陈龙［9］等讨论了时滞对具有天棚阻尼控制的1/4 汽车悬架模型的频响特性的影响，并计算了系统临界时滞的大小。Jalili［10］根据稳定性分析提出一种包含作动器时滞的车辆悬架系统优化方法。Shin［11］利用定性和定量的方法分析了时滞对系统稳定性的影响。

在目前的时滞稳定性研究中，大多数都是针对汽车悬架系统进行的，而以更加复杂的铁道车辆悬挂系统的时滞稳定性为研究对象的还很少见。本文对包含一系阻尼的铁道车辆1/4 动力学模型中存在的时滞稳定性问题进行分析，以期获得含时滞的悬挂控制系统失稳临界时滞的情况。

1 磁流变阻尼器天棚阻尼控制

作为半主动控制的实现载体，磁流变阻尼器有很多优点，如反应时间短(约0．1ms)，抗剪切强度高，对温度和外界环境不敏感，不存在明显的时滞问题，调节方便等优点［12］。磁流变阻尼器的力学模型有很多种，如Bingham 模型、Bouc-Wen 模型和多项式模型等。本文采用文献［13］中的用速度的指数函数和线性函数拟合磁流变阻尼的特性曲线，当电压为最大时阻尼力可表示为

式中，sign(x)为符号函数;V 为车体和悬挂之间的相对速度，即V = ˙x2- ˙x1;a 和b 为常数，反映了磁流变阻尼在高速时的饱和性以及在低速时的高阻尼性，可以通过实验获得。

在理想状态下，天棚阻尼控制下的磁流变阻尼器输出的可调阻尼系数为

式中，Cout为磁流变阻尼器输出的可调阻尼系数。

但在实际中，磁流变阻尼器输出的最小可调阻尼器系数并不能达到零值，而存在着所谓的基值阻尼C，即磁流变阻尼器实际输出的最小可调阻尼器系数为C。本文为了分析方便，将基值阻尼C 看作一个单独的阻尼器存在，而将磁流变阻尼器的输出可调阻尼系数写为

式中，Cr为调整后的磁流变阻尼器时实际输出可调阻尼系数。

2 含时滞的铁道车辆垂向模型

包括一系垂向阻尼的铁道车辆1/4 模型如图1 所示，速度通道内含时滞τ 的运动微分方程写为

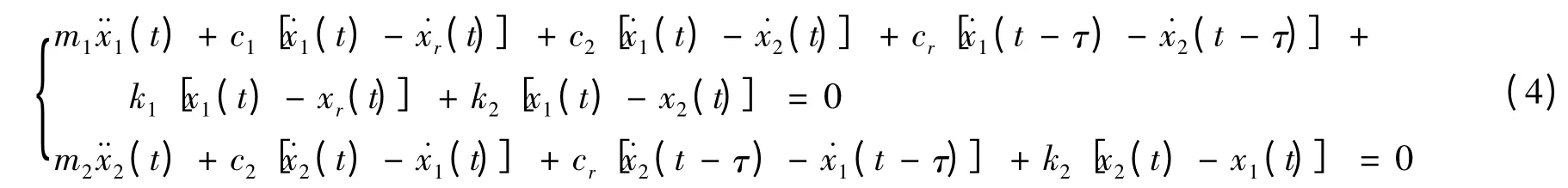
根据λ2M + λC + K 得到系统特征方程为

图1 1/4 车模型

系统失稳的临界条件是方程(6)有纯虚根，设纯虚根为λ = iω，带入方程(6)，并将指数函数转化为三角函数形式，然后分离实部和虚部，结果为

可以分别得到sin(ωτ)和cos(ωτ)的表达式

将式(8)带入sin2(ωτ)+ cos2(ωτ)= 1 中可以得到仅含未知数ω 的方程

可以通过求解方程(9)得到ω 的实根，带入式(8)可得临界时滞τ。如果方程(9)的根中没有实根，则系统进入全时滞稳定。

3 临界时滞稳定性分析

采用300 km 级高速动车组拖车车辆的参数进行计算，参数见表1。

表1 车辆系统参数

根据上述方法，可以绘得系统失稳临界时滞随可调阻尼变化的情况，如图2 所示。可以发现，当可调阻尼cr= 2 113 N·s/m 时，系统失稳临界时滞达到最大，为0．882 s。当可调阻尼cr＜2 113 N·s/m 时，方程(9)无实根，系统进入全时滞稳定状态。经过改变基值阻尼c2的大小，可以得到不同基值阻尼状态下，系统达到临界失稳时的可调阻尼和临界时滞的大小。计算表明，取任意基值阻尼时，只要满足cr-c2=113 N·s/m，系统就会达到临界失稳状态，如图3 所示。

图2 系统临界时滞随可调阻尼变化情况

图3 系统临界时滞随阻尼差值变化情况

以虚线为界，虚线左侧为系统全时滞区域，在此区域内无论时滞取多大的值，理论上系统均为稳定状态。虚线右侧为非全时滞区域，临界时滞曲线下方区域为系统稳定区域，临界时滞曲线上方为系统不稳定区域。

4 数值仿真分析

4．1 时滞对系统频响特性的影响

对特征矩阵(λ2M + λC +K)求逆，可以得到传递函数矩阵G(λ)，那么λG(λ)则代表¨x2到˙xr的传递特性，将λ = iω 带入，即可得到其复频响应函数矩阵，即

根据式(10)，可以绘出时滞对幅频特性和相频特性的影响情况，选取可调阻尼系数cr= 8 000 N·s/m，此时的系统失稳临界时滞为0．474 6 s，任意选取时滞τ = 0．1 s，τ = 0．3 s 和τ = 0．5 s 的情况下进行说明，如图4 所示。从图中可以看出，时滞对系统一阶共振峰值(f = 0．537 Hz 处)的影响很大，而对系统二阶共振峰值(f = 4．965 3 Hz 处)的影响却很小。当时滞超过系统失稳临界时滞时，一阶共振峰值趋于无穷大，系统发生失稳。

图4 时滞对系统频响特性的影响

4．2 仿真分析

分别考察在确定性激励和轨道不平顺随机激励作用下，时滞对系统动力学特性的影响。根据方程(4)设计Simulink 框图，如图5 所示。参数根据表1 选取，取cr= 18 000 N·s/m，此时系统失稳临界时滞为0．371 9 s。

考察随机激励作用下的情况。本文采用基于频域功率谱采样的数值模拟方法生成德国高干谱轨道不平顺曲线［14］，如图7 所示。仿真车辆以250 km/h 的速度行驶在德国高干扰轨道上，考察轨道不平顺随机激励作用下的车体分别在时滞τ = 0 s，τ = 0．3 s 和τ = 0．5 s 时的振动加速度情况，如图8 所示。从图中可以发现，随着时滞量的增加，车体振动加速度增大，当时滞超过系统失稳临界时滞量时，车体振动加速度曲线发散，系统失稳。

5 结论

本文基于含时滞的线性常微分方程临界时滞理论分析，采用数值方法讨论了时速300 km 级高速动车组的失稳临界时滞大小，分析了不同区域的稳定性状态，然后分析了不同时滞状态下的系统频响特性，并对确定性激励和轨道不平顺随机激励作用下的车体振动情况进行了仿真分析。研究结果表明，时滞对系统一阶共振的影响较大，当时滞超过理论计算临界时滞时，车体振动加剧，系统发生失稳。

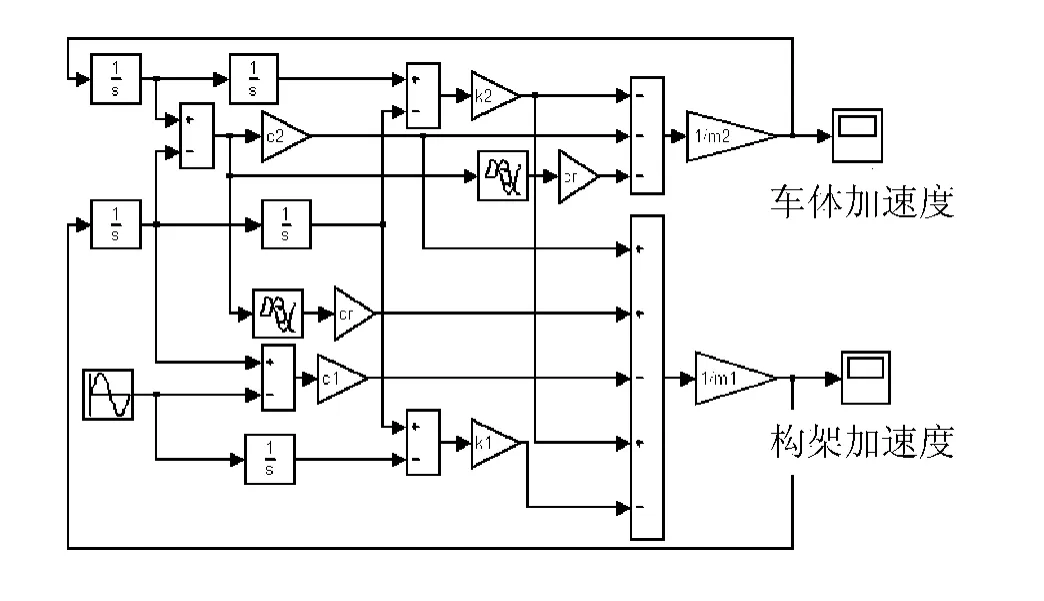
图5 时滞系统Simulink 框图

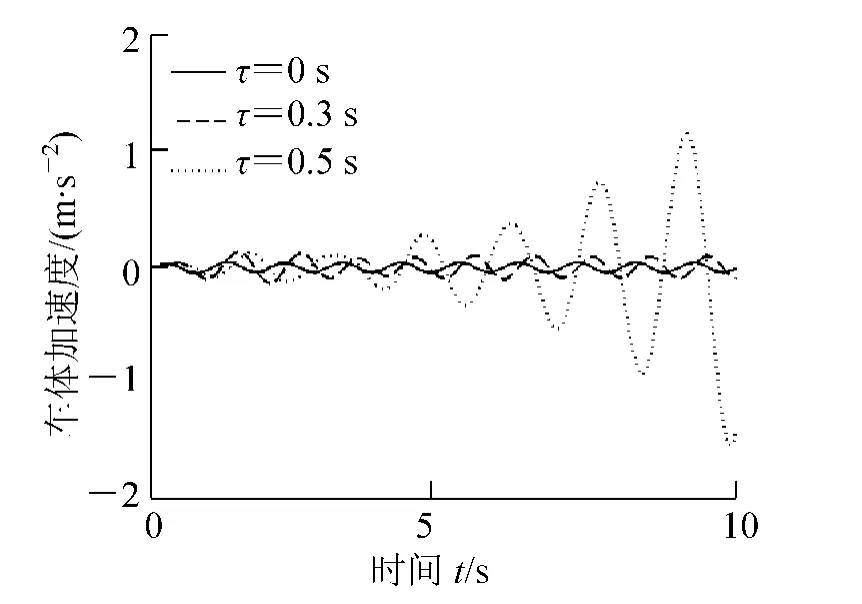
图6 正弦激励下时滞对振动的影响

图7 生成的德国高干扰随机不平顺

图8 随机激励下时滞对振动的影响

［1］刘永强，杨绍普，廖英英，等．基于MR 阻尼器的高速动车组悬挂系统半主动控制仿真［J］．振动与冲击，2010，29(12):97-101．

［2］Giua A，Melas M，Seatzu C，et al．Design of predictive semiactive suspension system［J］． Vehicle System Dynamics，2004，41(4):277-300．

［3］廖英英，刘金喜，刘永强，等．半主动控制与时滞对高速铁道车辆平稳性、稳定性及安全性的影响［J］．振动与冲击，2011，30(6):58-62．

［4］张曙光．高速列车设计方法研究［M］．北京:中国铁道出版社，2009．

［5］Wang ZH，Hu HY．Stability switches of time-delayed dynamic systems with unknown parameters［J］．Journal of Sound and Vibration，2000，233(2):215-233．

［6］Wang ZH，Hu HY．Dimensional reduction for nonlinear time-delayed systems composed of stiff and soft substructures［J］．Nonlinear Dynamics，2001(25):317-331．

［7］张文丰，翁建生，胡海岩．时滞对车辆悬架天棚阻尼控制的影响［J］．振动工程学报，1999，12(4):486-491．

［8］翁建生，张文丰，胡海岩，等．时滞天棚阻尼控制的车辆悬架系统特性研究［J］．南京建筑工程学院学报，1999(3):1-6．

［9］陈龙，汪若尘，江浩斌，等．含时滞半主动悬架及其控制系统［J］．机械工程学报，2006，42(1):130-133．

［10］Jalili N，Esmailzadeh E． Optimum active vehicle suspensions with actuator time delay［J］． Transactions of the ASME，2001，123:54-61．

［11］Shin KG，Cui XZ．Computing time delay and its effects on real-time control systems［J］．IEEE Transactions on Control Systems Technology，1995，3(2):218-224．

［12］刘永强，杨绍普，申永军．基于磁流变阻尼器的汽车悬架半主动相对控制［J］．振动与冲击，2008，27(2):154-156，161．

［13］Yao GZ ，Yap FF，Chen G，et al． MR Damper and its application for semi-active control of vehicle suspension system［J］．Mechatronics，2002(12):963-973．

［14］陈果，翟婉明．铁路轨道不平顺随机过程的数值模拟［J］．西南交通大学学报，1999，34(2):138-141．