弯扭联合作用下钢-混凝土组合箱梁受力特性的试验研究
张彦玲, 葛 威, 侯忠明, 张德莹
(1.石家庄铁道大学 土木工程分院,河北 石家庄 050043;2. 石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室,河北 石家庄 050043;3.北京交通大学 土建学院,北京 100044)
0 引言
钢-混凝土组合梁桥具有承载力大、高跨比小、节省材料、施工方便等优点,在中等跨度桥梁中得到了广泛采用。目前对于钢-混凝土组合梁桥,对其竖向荷载作用下的抗弯性能已进行了较为细致的研究[1-4],但是当组合梁应用于立交线路中时,由于线形的需要,经常设计为平曲线,此时由于梁轴本身的曲率效应,以及车辆荷载的偏心,都会在梁体中产生弯扭耦合效应。但目前在我国乃至其它各国规范中,都尚未给出能准确预测曲线组合梁力学性能的计算方法。
关于曲线组合梁受力性能的最早的试验研究是1973 年Colville[5]所做的四片简支曲线组合梁,试验中给出了曲线组合梁栓钉的简化设计方法。1999 年Thevendran et al[6-7]对5 片不同曲率的简支曲线组合梁进行了模型试验和非线性分析,发现曲线组合梁的承载能力随跨度与弯曲半径的比值的增大而减小。2008 年聂建国 等[8]进行了9 根钢-混凝土组合箱梁的扭转试验,建立了适于分析钢-混凝土组合箱梁复合弯扭强度的三维桁架模型。2009 年Tan et al[9-10]分别对6 片偏心加载的简支直线组合梁和8 片简支曲线组合梁进行了试验研究,给出了简支曲线组合梁的弯扭相关关系曲线。
以上研究主要集中在钢-混凝土组合工字型梁的研究上,在确定钢-混凝土组合箱梁弯扭相关关系时试验数据还比较缺乏。针对在钢-混凝土组合梁桥中应用比较广泛的箱型截面组合梁,通过弯扭联合作用下的静载模型试验,对其弯扭特性进行了试验研究。
1 试验设计及加载方案
1.1 试验内容
试验以钢-混凝土组合箱梁为研究对象,设计参数为初始扭弯比(初始扭矩与弯矩的比值)及栓钉剪力连接度,试验内容包括:(1)组合箱梁的破坏形态、极限承载力及破坏阶段的弯扭相关关系研究;(2)抗弯刚度和抗扭刚度研究;(3)不同荷载水平下截面应变沿截面高度和宽度方向的分布规律研究;(4)钢梁与混凝土板之间沿梁轴的纵向相对滑移和垂直于梁轴的横向相对滑移的规律研究。
1.2 试验设计与制作
根据不同的剪力连接度及初始扭弯比,共设计了6 片长度为4.5 m,计算跨径为4.2 m 的钢-混凝土简支组合梁,其中3 片为完全连接组合梁,3 片为剪力连接度为60%的部分连接组合梁。6 片组合梁截面尺寸相同(见图1),钢梁均采用Q235 钢,混凝土均采用C30,混凝土板内钢筋均采用HRB235,其中纵筋为6.5@130mm,箍筋为6.5@110 mm,栓钉为13 ×50 mm。完全连接的组合梁FCB、FCB1 和FCB2 梁在剪跨区内栓钉间距为120 mm,跨中区域为140 mm;部分连接的组合梁PCB、PCB1 和PCB2 梁栓钉沿轴向均匀布置,间距为210 mm,见图1。

图1 组合梁布置图(单位:mm)
1.3 试验装置及加载方案
试验加载分为中心对称两点加载(FCB 梁、PCB 梁)、斜对称两点加载1(FCB1 梁、PCB1 梁:偏心位置距梁纵向轴心垂直距离为135 mm)和斜对称两点加载2(FCB2 梁、PCB2 梁:偏心位置距梁纵向轴心垂直距离为270 mm)三种工况,如图2 所示。对6 片试验梁进行分级连续加载,荷载等级为10 kN。

图2 试验加载示意图
2 试验过程和结果分析
2.1 破坏过程及受力特性
对6 片试验梁进行分级连续加载至破坏,得到各梁一侧加载点的弯矩-曲率曲线和弹性扭矩-扭率曲线分别见图3 和图4。

图3 弯矩-曲率曲线图

图4 弹性扭矩-扭率图
由图3 可知,6 片试验梁在弹性阶段的受力特征差别不大,剪力连接度和初始扭矩的大小并未明显影响试验梁在加载初期的抗弯刚度,但在进入弹塑性阶段之后,各片梁在极限承载力和延性方面表现出较大的差异。总体来说,完全连接的三片试验梁,无论其扭弯比大小,其极限承载力和延性性能均明显优于部分连接的三片试验梁,其中完全连接的纯弯梁FCB 在整个加载过程中的受力特征发展最完善,屈服点明显,破坏之前变形大,有充分的延性发展;扭弯比最大的部分连接试验梁PCB2,其极限承载力和延性性能均最低,在钢材及混凝土应变均未达到屈服的情况下,已由于栓钉的大部分剪断而出现了连接滑移破坏,表现出明显的脆性破坏特征。但扭矩的存在对于组合梁极限承载力和极限弯矩的影响并不明显。
从图4 可以看出,在弹性阶段,初始扭弯比和抗剪连接度的大小对组合梁的扭转特性都产生了一定的影响。对于抗剪连接度相同的试验梁(FCB1 梁和FCB2 梁、PCB1 梁和PCB2 梁),扭弯比大的试验梁其抗扭刚度较扭弯比小的试验梁小;对于扭弯比相同的组合梁(FCB1 梁和PCB1 梁、FCB2 梁和PCB2 梁),由于栓钉不能有效地约束混凝土板和钢箱梁之间的连接以抵抗扭转变形,因此部分连接的组合梁其抗扭刚度明显小于完全连接的组合梁。
2.2 应变测试结果
(1)纵向应变沿截面竖向的分布规律。各试验梁跨中截面纵向应变沿竖向的分布规律见图5。由图5 可知,对于完全连接的组合梁,钢梁与混凝土之间的结合面滑移量较小,在0.8Pu 之前,跨中截面的纵向应变沿截面高度方向均近似保持为直线分布,基本符合平截面假定。部分连接的组合梁由于栓钉较少,不能有效地抵抗钢梁与混凝土板之间的相对滑移,竖向应变在结合面处有很长的一个水平台阶,且随荷载增加滑移量逐渐增大。但在0.8Pu 之前,台阶上下混凝土板和钢梁仍各自保持近似直线分布。
美国科技界认为会聚已经成为推动生物科技革命的战略思想和方法,代表了未来科研发展的新方向。理论界不仅分析了会聚项目的前沿性、社会性,也探讨了新型科研组织形式以及会聚研究发展可能带来的社会影响。这既是对科技潜在前沿的探索,也是对科技自身发展方式的思考,体现了美国科技界居安思危、进一步求新求变、先发制人的战略思维。

图5 跨中截面竖向应变
(2)主应变随荷载的变化规律。各试验梁跨中截面的主应变随荷载的变化规律如图6 所示,由于各试验梁均非纯扭构件,跨中截面都在弯矩或弯扭联合作用下,故混凝土板的主拉应变和主压应变并不对称,而是混凝土板均以主压应变为主。完全连接的FCB 梁、FCB1 梁和FCB2 梁混凝土板在跨中截面主压应变的发展都比较充分,在破坏时都接近了混凝土的极限压应变。部分连接的试验梁其跨中截面混凝土板规律与完全连接的试验梁相同,只是在破坏时最大主应变都比完全连接的组合梁小,这是由于出现了连接滑移破坏,使最终材料强度的发展不充分。
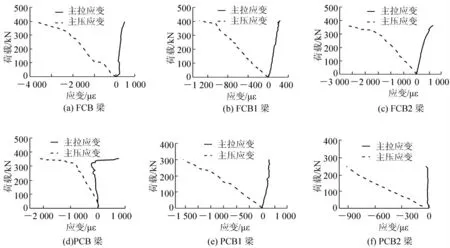
图6 试验梁跨中截面主应变
2.3 滑移测试结果
2.3.1 沿梁轴的纵向滑移
6 片试验梁梁端纵向滑移随荷载的变化曲线如图7 所示。

图7 荷载-滑移曲线图
由图7 可知,完全连接的3 片试验梁FCB 梁、FCB1 梁和FCB2 梁其界面抗剪滑移刚度和破坏时梁端的最大滑移量均明显大于部分连接的PCB 梁、PCB1 梁和PCB2 梁;当抗剪连接度相同时,随初始扭弯比的增大,破坏时梁端的最大滑移量未表现出确定性规律,但滑移刚度则随初始扭弯比的增大有所减小。
各试验梁滑移变形沿梁轴纵向的变化规律见图8,各图中滑移的4 个测点沿梁轴分别在南侧腹板的梁端位置、距梁端L/6 位置、加载点位置(距梁端L/3 处)和跨中位置。
由图8 可以看出,各试验梁的滑移量随荷载的增加逐渐增大,但滑移变形沿梁轴的分布规律均基本相同,在跨中至加载点之间的纯弯段内,由于剪力为0,故滑移很小;在加载点至梁端的弯剪段内,滑移量较大。由于剪力在该区域内均匀分布,故各测点滑移量基本相同,但略有差别,最大滑移量并未出现在梁端,而是出现在距梁端L/6 位置处的测点上,且6 片试验梁均表现出相同的规律。说明钢-混凝土简支组合梁的界面滑移规律完全遵循其截面竖向剪力沿梁轴的分布规律。
2.3.2 垂直于梁轴的横向滑移
对弯剪扭联合作用下的FCB1 梁、FCB2 梁、PCB1 梁和PCB2 梁,在纵向滑移的各相应测点布置了百分表,测试该位置钢梁与混凝土界面的横向滑移量。加载点位置界面横向滑移随荷载变化规律见图9。

图8 纵向滑移图
由图9 可以看出,加载点处组合梁界面上除纵向滑移外,还存在横向滑移,且随荷载的增大而增大。与纵向滑移相同,在加载初期,也表现出一定的弹性性能,随后曲线变得弯曲,进入弹塑性阶段,最后曲线出现缓平段,进入破坏阶段。横向滑移的大小将会对组合梁的抗扭刚度和承载力,以及在动力荷载作用下的横向振动特性产生影响。但由图9 还可以看出,由于各试验梁的最大横向滑移量还包括弯曲变形时横向泊松比的影响,故其随扭弯比的变化没有明显的规律;另外,剪力连接度对各试验梁的界面最大横向滑移也产生了一定的影响,剪力连接度小的试验梁横向滑移明显偏大。
各试验梁横向滑移变形沿梁轴纵向的变化规律见图10。由图10可知,在反对称的扭矩作用下,横向滑移沿梁轴的分布规律与纵向滑移差别很大。由于跨中截面位于反对称扭转变形的反弯点,而支座截面的滚轴支座也提高了抗扭约束,故这两处截面基本不发生扭转,横向滑移基本为0;在加载点位置,截面扭转角最大,横向滑移也出现最大值。说明钢梁与混凝土板结合面上的横向滑移量与扭矩作用下截面的扭转角存在一定的比例关系,但由于材料泊松比和测试误差的影响,这一结论尚需更多的试验结果支持。

图9 荷载-横向滑移曲线

图10 横向滑移图
3 结论
以钢-混凝土简支组合箱梁为研究对象,以初始扭弯比和剪力连接度为试验参数,对6 根试验梁进行了弯扭联合作用下的模型试验,重点研究弯扭联合作用下组合箱梁的弯扭受力特性,主要结论如下:
(1)完全连接的3 片试验梁,无论其扭弯比大小,其极限承载力和延性性能均明显优于部分连接的3片试验梁,表现为受弯破坏或弯扭破坏特征,而部分连接的试验梁则基本都表现为滑移破坏特征;扭矩的存在对组合箱梁极限承载力和极限弯矩的影响不大;在弹性阶段,连接度相同时,初始扭弯比大的试验梁抗扭刚度偏小;扭弯比相同时,部分连接的组合梁其抗扭刚度明显小于完全连接的组合梁。
(2)完全连接的组合梁界面相对滑移量较小,部分连接的试验梁沿截面高度的纵向应变图上则普遍在界面位置存在水平台阶,且随荷载增加滑移量逐渐增大;在弯扭联合作用下,混凝土板与钢梁的主拉应变和主压应变发展不对称,混凝土板均以主压应变为主,钢梁均以主拉应变为主。
(3)钢-混凝土组合箱梁在弯扭联合作用下,其钢梁与混凝土板结合面上既存在沿梁轴的纵向相对滑移,也存在垂直于梁轴的横向相对滑移。纵向滑移规律基本遵循其截面竖向剪力沿梁轴的分布规律;在反对称的扭矩作用下,横向滑移量随截面扭转角的增大而增大。
[1]樊健生. 钢-混凝土连续组合梁的试验及理论研究[D]. 北京:清华大学土木系,2003.
[2]张彦玲. 钢-混凝土组合梁负弯矩区受力性能及开裂控制的试验及理论研究[D]. 北京:北京交通大学土木建筑工程学院,2009.
[3]HOU Wenqi,YE Meixin. Design methods of headed studs for composite decks of through steel bridges in high-speed railway[J]. J. Cent. South Univ. Technol. ,2011,18(3):946-952.
[4]张彦玲,李运生,樊健生.连续组合梁弯矩重分布特征及其随荷载的变化规律[J]. 中南大学学报:自然科学版,2011,42(2):449-455.
[5]Colville J. Tests of curved steel-concrete composite beams[J]. Journal of the Structural Division,ASCE,1973,99:1555-1570.
[6]Thevendran V,Chen S,Shanmugam NE,et al. Nonlinear analysis of steel-concrete composite beams curved in plan[J]. Finite Elements in Analysis and Design,1999,32:125-139.
[7]Thevendran V,Chen S,Shanmugam NE,et al. Experimental study on steel-concrete composite beams curved in plan[J]. Engineering Structures,2000,22:877-889.
[8]聂建国,唐亮,胡少伟,等 钢-混凝土组合箱梁的抗扭强度[J]. 土木工程学报,2008,41(1):1-11.
[9]Tan E L,Uy B. Experimental study on straight composite beams subjected to combined flexure and torsion[J]. Journal of Constructional Steel Research,2009,65:784-793.
[10]Tan E L,Uy B. Experimental study on curved composite beams subjected to combined flexure and torsion[J]. Journal of Constructional Steel Research,2009,65:1855-1863.

