基于ANSYS 的钢管混凝土拱桥吊杆二次张拉力确定

路大鹏

(中铁十局集团，山东 济南 250000)

为了使拱桥成桥后达到合理成桥状态，系杆拱桥的施工通常对吊杆采用二次张拉的工艺，使成桥后吊杆力达到设计值，可见吊杆的张拉控制是系杆拱桥施工过程中非常关键的一步，直接影响系杆拱桥的正常使用以及服役年限。在拱桥施工过程中，吊杆的逐步张拉伴随着拱肋和主梁的变形，整个拱桥结构的变形与受力变化十分复杂。因此在吊杆二次张拉中，确定每步张拉的施工张拉力，使所有吊杆张拉完成后内力符合设计要求就显得非常重要，也是拱桥施工控制中最为复杂的一个环节。当前，多数确定二次张拉时施工张拉力的方法都基于影响矩阵法原理［1-4］，其核心就是影响矩阵的形成，但是多数形成影响矩阵的方法都非常繁琐［5-6］，这在一定程度上给计算人员带来许多不变。虽然也有文献曾提出一些形成影响矩阵的简便方法，但是并没有经过实例验证［7］。针对以上问题，以一座80 m 的铁路系杆拱桥为研究对象，首先基于ANSYS 有限元分析软件，利用正装迭代法对吊杆的初张拉过程进行了详细的模拟，得到二次张拉前各吊杆内力;然后介绍了利用ANSYS 对单元的降温功能形成影响矩阵的方法，计算出二次张拉时每步张拉的施工张拉力;最后利用正装法对二次张拉过程进行模拟，得到成桥后吊杆力符合设计要求，这说明得到的施工张拉力是合理的，验证了降温法形成影响矩阵的正确性。

1 工程背景

大桥结构为钢管混凝土系杆拱结构，计算跨径80 m，梁长83 m，主梁采用箱形截面，拱肋为钢管混凝土结构，哑铃型断面，拱轴线为悬链线，拱肋与主梁的刚度之比为，属于刚性系梁刚性拱。

全桥共设14 对吊杆，除拱脚至第一对吊杆间距为7．5 m 外，其余吊杆中心纵向间距为5 m;吊杆下端采用LZM7-61 型冷铸锚与主梁锚固，上端采用在拱肋顶部开孔的方式锚固;采用61 根 的平行钢丝束，钢丝采用PESFD7-61 新型低应力防腐索体;吊杆自左到右顺次编号如图1 所示。主要施工工序为:分段浇筑预应力混凝土连续梁;拱架上拼装钢箱拱，卸拱架;安装吊杆并采用图1 所示跳张法初张拉吊杆;施加二期恒载;按顺序对吊杆进行二次调整张拉。

2 有限元建模

基于ANSYS 分析软件采用空间梁单元建立钢管混凝土拱桥的“鱼骨刺”模型，利用生死单元技术对吊杆张拉过程进行模拟。有限元模型如图2 所示。

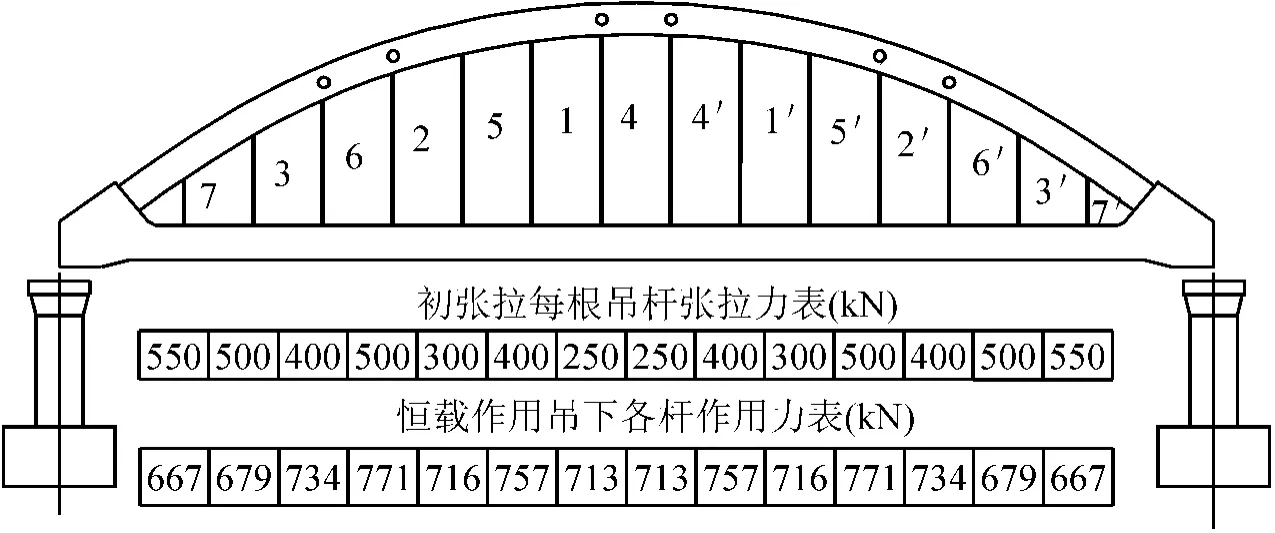
图1 吊杆初张拉顺序及张拉力

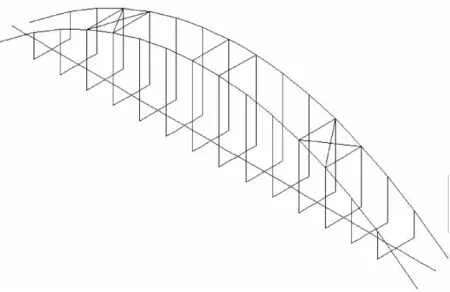
图2 有限元模型

拱肋和主梁均采用空间梁单元进行模拟，由于拱肋是由钢管与混凝土两种材料构成，建模时利用ANSYS 的组合截面技术自定义钢管混凝土哑铃型截面，梁体混凝土强度等级为C55，拱肋、横撑和斜撑内灌混凝土采用C55 补偿无收缩混凝土，材料特性参数参照相应规范设置;吊杆采用LINK8 单元模拟，抗拉强度标准值1 670 MPa，弹性模量205 GPa，吊杆与主梁的连接采用刚臂模拟，理论上只要将刚臂的刚度设为无穷大即可，但是考虑到模型计算的收敛性，只要将其适当放大即可;边界条件采用固结模拟。

全桥总共划分为123 个单元，其中95 个梁单元，28 个杆单元，主梁划分23 个梁单元，拱肋划分30 个梁单元。计算荷载:结构自重按《铁路桥涵设计基本规范》(TB10002．1—2005)采用，二期恒载(100 kN/m)包括道渣、电缆槽、防撞墙和人行道栏杆等。

由于有限元模型是在拱桥实际结构简化的基础上得到的，因此有限元模型很难在重量上与实际结构相等，这就需要对有限元模型中拱桥各部分的材料参数进行修正，本文采用重量等效原理进行修正，按照设计图纸中给出的理论重量来换算有限元模型中材料的容重。例如设计图纸箱梁总重为23 597．6 kN，而修正前模型中箱梁混凝土容重为25 kN/m3，箱梁总重为17 105 kN，要是模型在重量上与实际箱梁相等，需要把模型中箱梁混凝土容重修正为34．5 kN/m3，模型中拱肋混凝土和钢材的容重采用相同方法进行修正。

3 吊杆张拉过程模拟

按施工图要求，吊杆分为7 组，采用跳张法进行张拉，张拉顺序为:1、1＇号;2、2＇号;3、3＇号;4、4＇号;5、5＇号;6、6＇号;7、7＇号，具体张拉顺序及控制张拉力如图1 所示。有限元模拟时，吊杆初张拉应严格按照吊杆张拉顺序进行。采用正装迭代法模拟吊杆初张拉过程。

3．1 迭代法确定单根吊杆张拉力

在ANSYS 中采用调整初应变的方法迭代求解吊杆张拉力，实际结构中由于吊杆张拉后拱肋和主梁均产生变形，使得目标吊杆力F ≠EAε ，{ε}为吊杆初应变。迭代法通过不断改变赋予吊杆的初应变来使吊杆达到目标吊杆力。文献［8］利用ANSYS 二次开发技术，开发了基于迭代法的斜拉桥调索程序，拱桥吊杆力迭代计算思路与斜拉桥调索过程相似。

3．2 按设计顺序模拟吊杆初张拉

使用迭代法按初张拉顺序依次张拉吊杆，完成初张拉。吊杆的张拉伴随着拱肋和主梁的变形，初张拉过程中吊杆力的变化十分复杂，后期张拉的吊杆直接影响前期张拉吊杆的内力。当第i 批吊杆张拉完

成后，只有该批吊杆吊杆力为设计初张拉吊杆力。初张拉过程中吊杆力理论值变化详见表1。

表1 吊杆初张拉过程中吊杆力理论值变化 kN

4 影响矩阵法原理

在系杆拱的二次张拉中，吊杆是分批逐步张拉的，前期和后期张拉的吊杆力是相互影响的，即需要吊杆力的空间影响效应。在对二次张拉进行控制时，可以根据前期各批张拉的吊杆对本阶段待张拉吊杆的影响，利用影响矩阵法确定本阶段吊杆力的调整量。

系杆拱二次张拉的影响矩阵法，利用广义矩阵的概念，将吊杆力目标变化量用吊杆力调整量和影响矩阵表示，如果认为在调整阶段拱桥满足线性叠加原理，可以建立以下方程

求出吊杆力调整量，进一步求出吊杆力分批调整时各批的调整量。式中，{F0}为二次张拉前各吊杆吊杆力向量;{F}为设计成桥吊杆力向量，即目标吊杆力向量，{F}- {F0}为调值向量;{ΔP}为被调向量;［A］为影响矩阵。

式中，{A}i= (a1ja2j… aij… ajj)T为影响向量，被调向量中第j 个元素发生单位变化引起调值向量的变化向量;aij为第j 批吊杆内力发生单位变化对第i 批吊杆内力的影响量，即第j 个施调变量发生单位变化对第i 个调值变量的影响量。

在系杆拱的二次张拉中，调值向量和被调向量均取吊杆力向量，在确定了{F0}、{F}、［A］后，求解方程就可以得到被调向量。

5 二次张拉施工张拉力的确定及应用

(1)在ANSYS 中计算吊杆张拉力影响矩阵法。由上所述，在影响矩阵法确定二次张拉力过程中，关键是求出影响矩阵，目前常用的方法有:基于强迫变形的影响矩阵法［5］;基于结构连续变更定理生成影响矩阵［6］。虽然这两种方法相对于修改总刚度矩阵法［1］简便不少，但是生成影响矩阵的过程仍旧非常繁琐。本文基于ANSYS 分析软件，提出采用降温法生成影响矩阵，具体过程如下:

为形成对角元素为aii= 1 的影响矩阵，必须使吊杆力发生单位变化，在ANSYS 中需要经过两步计算:第一步，预先给某吊杆降温1 ℃，经求解后，该吊杆内力变为F;第二步，直接给该吊杆降温1 000/F℃，求解后，该吊杆最终内力为1 kN。

利用以上方法，依次使第j(j = 1，2，…，14)(j 为张拉顺序号)批张拉的内力发生单位变化1 kN，得到14 个影响向量按张拉顺序组集得到吊杆张拉力影响矩阵。张拉顺序为一侧拱脚到另一侧拱顶逐对、两侧拱肋对称调整，即1 号;1＇号;2 号;2＇号;3 号;3＇号;4 号;4＇号;5 号;5＇号;6 号;6＇号;7 号;7＇号。结果如下:

以上过程可以看出采用降温法形成影响矩阵过程清晰简单，原理明确，容易理解和接受。

(2)计算二次张拉前吊杆力向量{F0}和目标吊杆力列向量{F}。按第3 节的正装法得到二次张拉前各吊杆力向量{F0};目标吊杆力列向量{F}即为设计成桥吊杆力列向量。

(3)求解方程(1)得到被调吊杆力列向量{ΔP}。

(4)按下式计算分批二次张拉时各吊杆施工张拉力

式中，Ni为第i 批吊杆施工张拉力;F0i为第i 批吊杆二次张拉前吊杆力;aij为影响矩阵［A］中对应的元素;ΔPi为第i 批吊杆被调吊杆力值，即对应被调吊杆力列向量{ΔP}中第i 行元素。文献［4］详细介绍了如何利用影响矩阵计算二次张拉各批吊杆施工张拉力的方法及计算公式。

(5)利用正装迭代法在ANSYS 中对吊杆二次张拉过程进行模拟，各批吊杆施工张拉力为(4)中计算得到的Ni，求解完成后得到成桥状态各吊杆内力与设计吊杆力相比较，以验证本方法的正确性，验证降温法形成影响矩阵的正确性。二次张拉阶段吊杆施工张拉力和成桥吊杆力见表2。

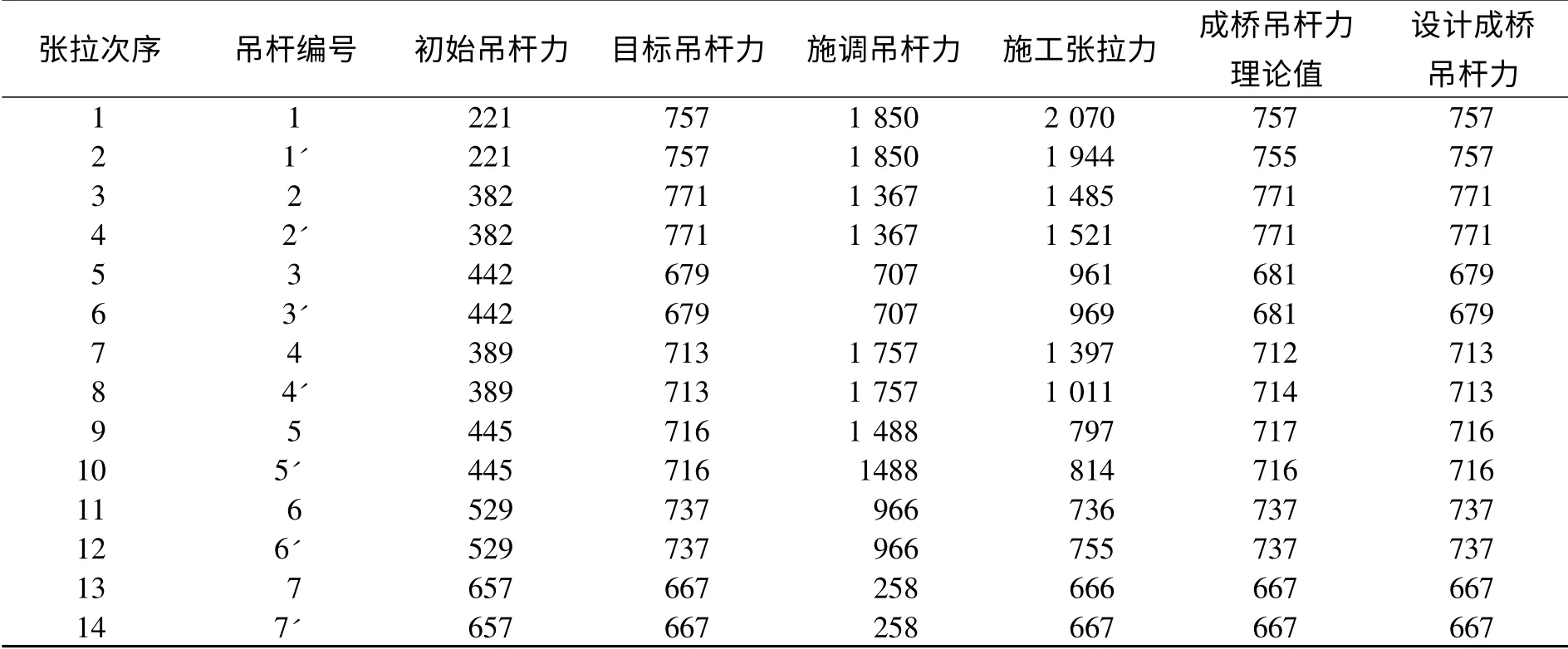
表2 二次张拉阶段吊杆施工张拉力及成桥吊杆力 kN

从表2 可以看出，利用正装迭代法在ANSYS 中模拟二次张拉过程后得到成桥状态下的吊杆力与设计吊杆力相比误差很小，这就验证了利用降温法生成影响矩阵的正确性，也验证了本文确定二次张拉力方法的正确性。1 号、1＇号、2 号、2＇号、4 号和4＇号吊杆二次施工张拉力较大，这使因为1 号、1＇号、2 号和2＇号是最先张拉的吊杆，后张拉的吊杆对其影响较大;而4 号和4＇号吊杆则是最靠近跨中的吊杆，由此可见，施工张拉力的大小与吊杆张拉顺序和位置均有关系，这也突出了吊杆力影响矩阵的重要性。

6 结论

本文提出的结合正装迭代法和影响矩阵原理计算二次张拉力的方法，原理明确，思路清晰，基于ANSYS 通用有限元分析软件建立拱桥的空间梁单元模型即可，计算简单。经验证降温法形成影响矩阵的方法，概念明确，计算简便，提高了计算二次张拉力的速度。该方法和思路也可以用于其他拱桥和斜拉桥，尤其是降温法形成影响矩阵应用于斜拉桥，可大大减少计算量，提高工作效率。

［1］刘邵平，段鸿杰，李求源．寒山大桥吊杆二次张拉索力计算［J］．现代交通技术，2011，8(1):28-31．

［2］谢瑞杰，任伟新．下承式钢砼系杆拱桥吊索施工张拉力计算［J］．中国西部科技，2010，9(11):10-11．

［3］陈淮，吴红升，唐军．蒲山系杆拱桥吊杆张拉力的空间计算分析［J］．铁道科学与工程学报，2008，5(2):12-15．

［4］盛兴旺，张同飞．系杆拱桥吊杆千斤顶张拉力确定方法及其应用［J］．铁道科学与工程学报，2010，7(3):11-15．

［5］汝诚，郭文复．结构关心截面内力、位移混合调整计算的影响矩阵法［J］．计算结构力学及其应用，1992，9(1):91-98．

［6］陈滋敏，王洪平，车维毅．悬索结构关心截面内力、位移的调整［J］．辽宁大学学报:自然科学版，1994，21(2):20-23．

［7］杨俊．基于影响矩阵的大跨桥梁合理成桥状态与施工控制研究［D］．武汉:武汉理工大学土木工程与建筑学院，2008．

［8］叶梅新，韩衍群，张敏．基于ANSYS 平台的斜拉桥调索方法研究［J］．铁道学报，2006，28(4):128-131．