法向接触刚度对装配体振动模态影响的研究

艾延廷，翟 学，王 志，乔永利

(沈阳航空航天大学 辽宁省数字化工艺仿真与试验技术重点实验室，沈阳 110136)

在工程领域，结构分析的研究对象往往是由众多零件、组件和部件经过装配而形成的机械系统。工程结构装配形式繁多，包括配合连接、螺栓连接、销连接、焊接、胶结、啮合连接等。在对装配体进行模态仿真和动力学分析时，由于结合面处理的技术问题，不得不对分析模型进行简化。如不考虑零件之间的连接配合关系，而是将装配体中的各个零件直接合并为一个整体，认为装配件之间是刚性连接。由于有预载荷的机械装配体(如螺栓法兰连接)的接触表面存在接触应力，不同的接触应力和接触面粗糙度，使接触面间形成分布不均匀的法向接触刚度，会对整个装配体的振动模态产生影响。刚性连结假设不能正确反映装配结构间的连接刚度和阻尼，其动力学特性计算结果往往与实际情况相差很大，无法实际应用。本文的研究起源于对航空发动机盘式拉杆转子各轮盘之间以及盘轴间的连接刚度对发动机转子的轴向和横向振动模态影响的分析。该方面的研究主要方法有两种，一是模态实验［1］，二是对部件做集中参数处理后通过键合图法［2-3］或有限元法［4-5］进行数值计算。随着发动机转子以及整机结构设计技术的发展，要求在设计初期即进行转子和整机的有限元建模，进而通过仿真实现其动力学优化设计。文献［1］提出的方法是对设计并加工出的实物模型进行实验模态分析，因而无法在设计之初进行模态计算与分析;文献［2-3］使用的键合图法与轮盘等结构的有限元模型无法联合使用。文献［4］采用有限元法中的接触单元进行接触刚度分析与模态计算。在一个装配体中，常常有多处采用螺栓联接结构，如在某型航空发动机转子两级盘-盘联接中有50余螺栓，如果对每个螺栓都进行有限元建模，则需要大量的计算机资源，造成大量的时间消耗，甚至计算机无法运行，因此，该方法的实际应用受到限制。文献［5］通过对传统的有限元方法进行改进，并编程计算，实现接触面接触刚度对转子动力特性影响的研究与分析。本文试图对带有预紧力的螺栓联接结构的接触刚度进行有限元等效计算，以便为工程中的螺栓联接有限元建模与仿真问题提供一个有效方法。

本文在静态接触分析的基础上，依据接触力学相关理论，根据接触面的粗糙度参数确定出接触刚度［6-7］;然后在有限元模型中加入实体层单元，通过改变实体层单元的弹性模量来等效接触刚度;最后再通过有限元方法对装配体进行模态分析。

1 接触刚度理论

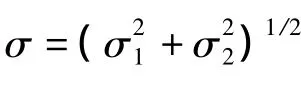
取表面的平均水平线为基准线，称刚性表面到基准距离为间隔d，称顶点到基准的距离为顶点高度zs。zs的平均值为，其概率密度函数为φ(zs)。如果在名义表面积A0中有N个顶点，则在间隔d处接触的顶点数为:

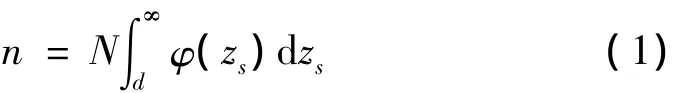
如果顶点高度超出了间隔，那么它将被压缩δ=zs-d，并且将在半径为a的小圆形区域中与平面构成接触。因此，第i个顶点具有的接触区域为:

压缩该顶点所需要的力可写成:

式中f(δ)和g(δ)与接触表面的材料性质有关。如果变形完全是在弹性极限之内，由Hertz方程有:

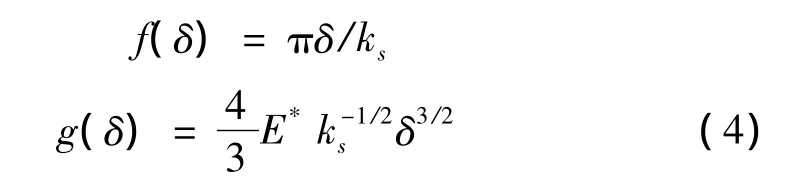
为了求出真实的总接触面积A和总的名义应力=P/A0，必须对高度超出间隔的所有凹凸起伏求和。于是有:

将式(4)代入式(5)，并进行归一化处理可得:

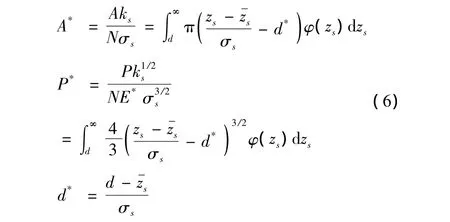
由式(6)可得接触刚度kc:

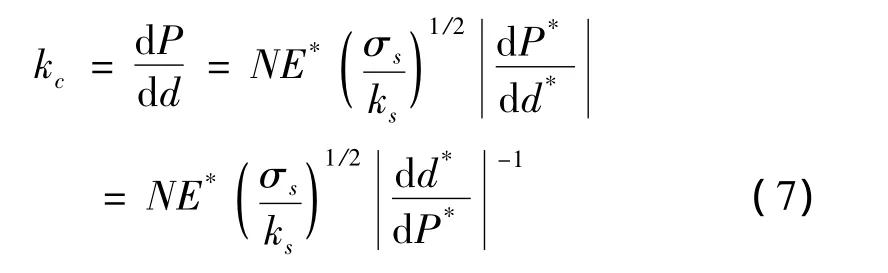
2 模型建立

2.1 接触刚度计算

许多实际的表面，特别是未处理过的基表面，其高度分布服从Gauss分布。对于标准偏差为σ的Gauss分布，顶点高度的分布非常接近Gauss分布，其标准偏差σs≈σ，顶点的高度位于表面的平均水平之上0.5σ～1.5σ之间;顶点曲率与该表面的均方根曲率量级相同，即=σk;如果波状表面是随机的各向同性表面，采用趋近于零的抽样间隔，则单位面积的顶点数为ηs=1.209，其中ηp为迹线单位长度上的峰点数，通过分析轮廓迹线中的峰点数确定。均值为zs，方差为σs的Gauss分布的概率密度函数为:

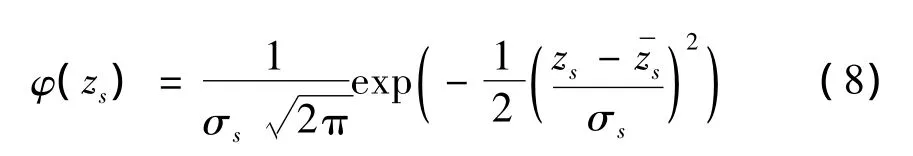
由式(6)和式(7)可得:

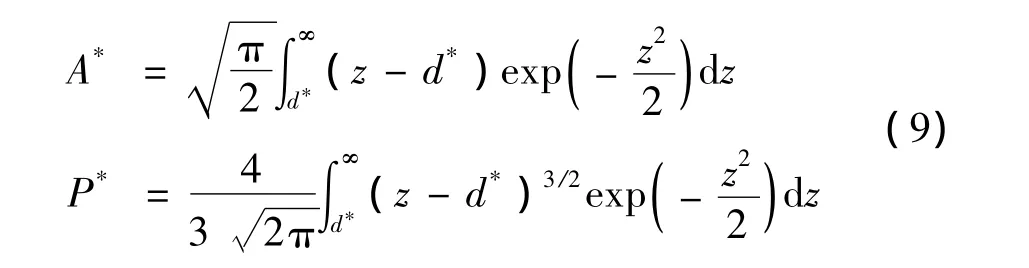
基于式(9)得到真实接触面积和归一化间隔随无量纲载荷的变化关系如图1所示。

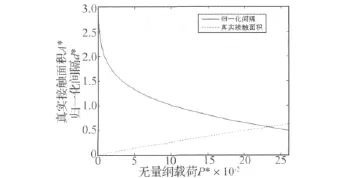
图1 真实接触面积和归一化间隔随无量纲载荷的变化Fig.1 The variation of real contact area and normal step as a function of dimensionless load

根据式(7)和图1，可以确定接触刚度。

上面接触刚度理论是基于假设每一个凹凸的变形与其相邻的凹凸无关。当实际接触面积与名义接触面积相比不再很小时，例如在归一化间隔小于0.5的地方，误差将加大。在另一端，如果归一化间隔大约超过3.0时，则使用统计方法来研究接触问题变得不精确。

2.2 有限元等效刚度建立

通用有限元计算软件能够对接触问题进行静力学分析，但是这些分析假定了接触面连续，对于包含粗糙度的接触面不能够进行分析。本文利用通用有限元软件计算出接触表面的接触压力;然后使用这些接触压力数据和接触表面的粗糙度以及接触部件的材料属性，根据接触力学的知识计算出接触表面每个单元的接触刚度;然后使用层单元，将接触刚度折算为层单元的弹性模量来修改模型。

折算的具体过程如图2所示。当具有名义面积A0的接触单元和下面的目标单元接触时。该法向接触刚度可等效为层单元的刚度，如图2所示。建模时比较方便的做法是将原来靠在一起的接触单元和目标单元移开一定距离h，可以取接触时的最大间隔值。等效公式为:

通过调节单元的弹性模量E'就可以等效接触刚度kc了。

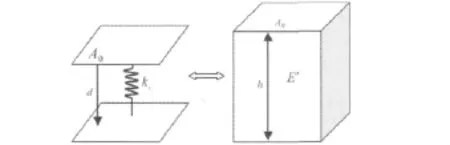
图2 使用层单元来模拟接触刚度Fig.2 Contact stiffness simulated with solid elements

由于不考虑切向接触刚度，材料的密度和泊松比都可以看做为0。接触面用层单元模拟，接触面的刚度用层单元弹性模量等效，层单元的厚度为h，层单元两端与原来实体的连结采用Nastran软件中的多点约束技术完成。

3 算例

3.1 接触刚度计算

本文研究的物理模型长l=10 mm，宽b=10 mm，截面面积A=100 mm2，高h=50 mm。材料参数为:弹性模量E=2.1e11 Pa，泊松比 μ =0.3，密度 ρ=7 850 kg/m3。接触面取在立方体的中间位置。立方体的下端面支撑在刚性水平面上，立方体的上端面施加压强108 Pa。

中间接触面的间隔即层单元的厚度h取1 mm。文献［4，7］使用静态实验和模态实验，并通过参数识别对类似结构的法向和切向接触刚度进行了测量。

3.2 基于解析解的模型固有频率计算

接触面间的接触刚度可以通过接触面间的接触参数的实验测量及其分布特征分析按上述公式计算。而接触刚度一旦确定，即可按层单元法和多点约束技术进行有限元分析与计算。计算的准确性，一般采用实验的方法对最终的模态分析结果进行验证，实际包含对接触刚度计算的准确性和有限元模型的准确性两方面的验证。本文假设接触刚度计算是准确的，只进行有限元模型的正确性验证。研究两个长立方体，其中间接触，接触刚度用弹性系数为kn的弹簧模拟，研究其纵向振动问题，建立图3所示力学模型。

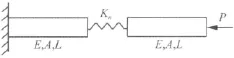
图3 计算的力学模型Fig.3 Mechanical model for calculation

根据有关知识，可以推导出:

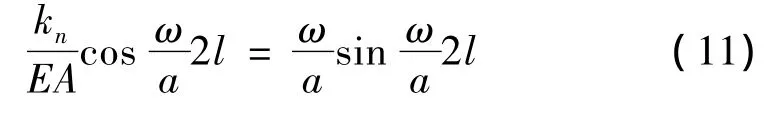
或:

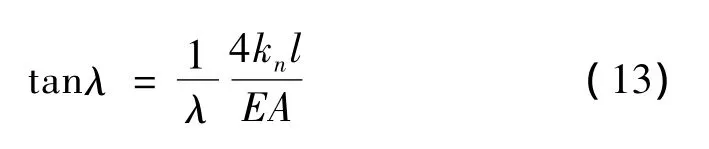
由式(13)，可以求出各阶固有频率的解析解。

3.3 基于有限元等效的振动模态计算

本文只分析结构在竖直方向的振动，所有节点水平方向约束。图4中的h取为1 mm。由式(10)计算出等效实体单元的弹性模量为E'=1.04×1010N/m2，这比上下立方体的材料的弹性模量要小，所以其固有频率比由上下立方体所构成的整体部件要低。表1列出了考虑法向接触刚度的等效模型解、整体有限元模型解与固有频率的解析解对比，可以看出，有限元等效模型解与解析解非常接近，而不考虑接触问题的整体模型解较有限元模型解误差大。

图5给出了二者前3阶振型的对比，不同的颜色代表不同的位移量，如在第一阶振型图中，颜色从蓝到红，对应振动位移从0到最大值1。由图5可以看出，等效模型与整体模型二者在振型上也存在差异。

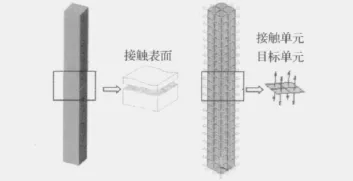
图4 物理模型(左)、有限元接触模型(右)Fig.4 Physical model(left)，element contact model(right)

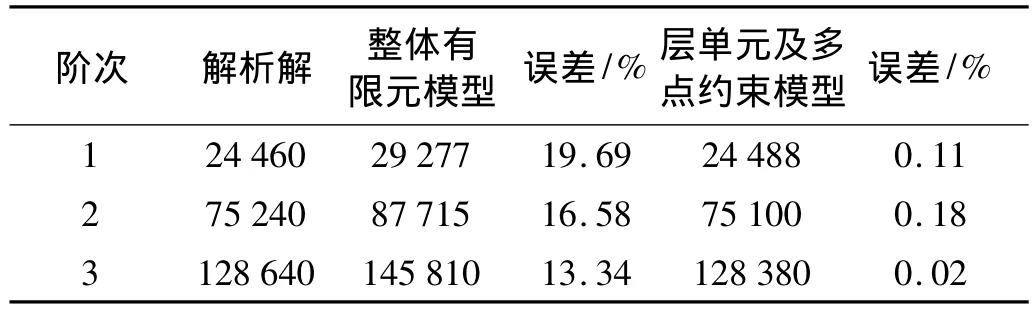
表1 考虑法向接触刚度的等效模型、整体有限元模型与固有频率解析解对比(Hz)Tab.1 Contrast of the frequencies for the equivalent model considering contact stiffness，the solid model and theoretical solution(Hz)

图5 等效模型(右)同整体模型(左)的前3阶模态振型对比Fig.5 Comparisons of the first three vibration models for the equivalent model(right)and solid model(left)

4 结论

本文探讨了在接触面间添加一层单元，通过改变实体单元弹性模量来建立考虑法向接触刚度对装配体振动模态影响的有限元模型。研究表明，不考虑法向接触刚度的有限元整体模型解较解析解误差很大，一般超过10%以上，且频率越低差异越大;而考虑接触刚度的有限元等效模型解与固有频率解析解差异很小，即只要接触刚度计算准确，本文提出的方法就能得到理想的计算结果，且计算简单、实用。另外，考虑与不考虑接触刚度，其各阶模态振型也存在一定差异，这主要是接触刚度单元的存在引起的。本文分析中假设了通过预载所形成的法向接触刚度在振动中一直保持不变，事实上，由于在振动中接触面间的接触间隔一直在改变，所以接触刚度也会跟着改变，这属于非线性振动模态范畴，下一步将要进行深入研究。本文的研究，有助于分析像发动机盘式拉杆转子这种连接刚度对系统振动模态影响较大的情况。

［1］施丽铭，张艳春.拉杆式模型转子固有频率的实验与计算研究［J］.振动与冲击，2008，27(S):47-49.

［2］王艾伦，骆 舟.拉杆转子轴向振动的动力学模型［J］.中国机械工程，2009，20(13):1524-1527.

［3］章圣聪，王艾伦.盘式拉杆转子的振动特性研究［J］.振动与冲击，2009，28(4):117-120.

［4］ Zheng Y，Rong Y，Hou Z.A finite element analysis for stiffness of fixture units［J］.Journal of Manufacturing Science and Engineering，2005，127:429-432.

［5］高 锐，袁 奇，高 进.燃气轮机拉杆转子有限元模型研究及临界转速计算［J］.热能动力工程，2009，24(3):305-308.

［6］饶柱石，夏松波.粗糙平面接触刚度的研究［J］.机械强度，1994，16(2):71-75.

［7］约翰逊K J.接触力学［M］.北京:高等教育出版社，1992.

［8］饶柱石.栏杆组合式特种转子动力学特性及其接触刚度的研究［D］.哈尔滨:哈尔滨工业大学，1992.

［9］Greenwood J A，Tripp J H.The contact of two nominally flat rough surface［J］.Pro.IMechE，1970，185:102-108.