考虑温度梯度的模态应变能法海洋平台损伤检测研究

刘克飞，石 湘，周 雷，王凤云

(1.中国海洋大学工程学院，青岛 266100;2.海洋石油工程股份有限公司，天津 300451)

导管架式海洋平台是海上石油开采普遍采用的结构型式，长期服役的这种平台结构通常是有损伤的，目前基于结构模态参数变化的平台结构整体损伤检测技术成为一个研究热点［1］。对于导管架海洋平台这样巨大的结构物，主要使用环境载荷下的振动信号进行模态识别和损伤检测，而环境温度是干扰识别和检测的一个重要因素。有研究表明对于钢筋混凝土大跨度桥梁结构模态频率与温度具有明显的季节相关性，其模态频率日平均值随着温度日平均值的升高而降低，并且在一年中可以发生1.5% ～2.0%的变化［2］，同时大跨度桥梁结构上不同部位存在的温度梯度对模态频率也有显著影响［3］。但是环境温度对海洋平台模态参数识别及损伤检测的影响目前尚没有研究。在海洋环境下，环境温度随季节变化很大，同时平台上部结构和水下结构也存在较大温差，温度的显著变化会造成结构材料弹性模量的变化，进而影响结构的模态参数及损伤检测。本文以一个导管架平台为模型，考虑了海洋环境温度垂直分布(温度梯度)对结构不同位置材料弹性模量的影响，研究了海水温度梯度对模态应变能法损伤检测的影响规律。

1 基本理论

1.1 海水温度梯度现象

海水温度梯度是海洋环境的重要参数之一，它反映了海水温度的垂直分布及其变化。影响浅层海水温度垂直分布的因素有很多，其中季节变化的影响尤为显著。在海洋的多数区域内，这种变化只限于200～400 m以内的比较薄的水层。图1例举了大西洋浅海某海域水温不同月份垂直分布曲线［4］，从图中可以看到春季和冬季水温随深度几乎没有变化，夏秋季节水温变化较为明显。尤其是在夏季，水温在0～80 m水深范围内降低了15℃左右，而且水面以上气温会比表层海水温度高5～10℃。以下的研究将以7月份这条梯度变化最大的曲线为依据，划分结构的环境温度梯度分布。

1.2 基于温度变化的钢材弹性模量变化

温度变化对结构动力特性的影响主要有两方面:一是温度变化会引起结构材料弹性模量的变化;二是温度变化会引起结构热胀冷缩，使结构尺寸变化或使超静定结构产生预应力。对于导管架式海洋平台，在竖直方向上为悬臂结构，结构热胀冷缩可以忽略不计，因此环境温度对海洋平台结构动力特性的影响主要体现在温度对钢材弹性模量的影响。试验证明，几乎所有的金属与合金的弹性模量都随温度变化而变化，一般随温度的增加而减小，在常温范围内可视为线性变化。机械设计手册给出了常用钢材在不同温度下的弹性模量［5］，以此为参考并为方便计算，取不同温度下钢材的弹性模量如表1，在0～25℃范围内弹性模量减少了 1.2%。

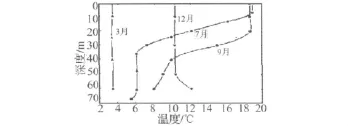
图1 大西洋浅海某海域水温季节变化Fig.1 Seasonal temperature variation of water in Atlantic shallow

表1 不同温度下钢材弹性模量取值Tab.1 Steel elastic modulus in different temperature

1.3 模态应变能损伤检测方法

模态应变能法是Kim［6］于1995年提出的一种损伤检测方法，并在2002年进行了改进。其基本思想是将结构分为一系列的单元，分别计算结构损伤前后每个单元的应变能变化率，而某些模态振型在结构损伤附近发生局部突变，故模态应变能在结构中的分布将发生变化，所以可以通过比较每一单元模态应变能的变化来进行结构损伤诊断。该方法非常适合于导管架平台这种框架结构，其基本算法如下:

对于一个有ne个单元的线性未损伤框架结构，结构的第i阶模态刚度可以表示为:

其中，Φi和K分别是第i阶模态向量和系统刚度矩阵。那么对应第j个单元的第i阶模态刚度表示为:

其中，Kj是第j个单元在整体坐标系下的刚度矩阵。

对于随后损伤的结构，把相应的模态参数带入到方程(2)中，用上标“*”表示损伤结构。则

借助结构有限元理论，方程(2)、(3)中的Kj和K*j可以写成如下形式:

其中参数Ej和分别表示单元j未损伤和损伤后的材料刚度特性，它们可被视为弹性模量，Kj0表示仅仅包含结构几何信息(有时包括泊松比)的单元刚度矩阵。Ej/可以被作为第j个单元的损伤检测指标，它可以被简单理解为损伤前后该单元的弹性模量之比。

假设结构在nd个位置发生损伤，则文献［6］推导出一种对于第i阶模态第j个单元的损伤定位指标，表示为:

其中:

同样上标“*”表示损伤结构，ne为结构单元总个数;gi表示因损伤引起的系统第i阶模态参数的变化:

其中dλi表示结构损伤前后的第i阶特征值λi与的差，即 dλi=λi-;dMi表示第i阶模态质量Mi的变化量，因为dMi所占权重较小且不易计算，本文中设dMi=0。那么对nm阶振动模态来说，第j个单元的损伤指标βj表示为:

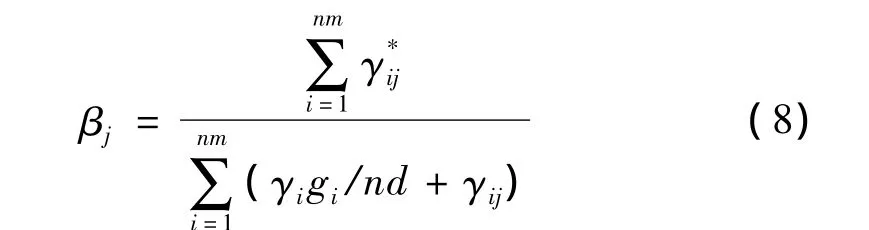
一旦第j个单元发生损伤，单元损伤程度评估指标为:

当第j个单元发生损伤时刚度减少，αj＜0。αj可以被理解为单元弹性模量变化率。

假设各单元的损伤指标βj符合正态分布，那么将损伤指标βj标准化将得到鲁棒性更好的损伤定位统计指标:

然后通过一个统计模式识别技术对损伤模式进行分类识别，结构损伤位置的判定准则被确定如下:

当Zj＜Zc时，结构在第j个单元没有发生损伤;

当Zj≥Zc时，结构在第j个单元发生损伤;

其中Zc是反映统计意义水平的一个参数，在以下的数值算例中取Zc=2，可信度水平为97.7%。另外使用指标αj评估损伤程度，0＞αj＞-1，表示损伤程度在0～100%之间。

2 数值模拟

2.1 平台初始有限元模型

平台模型以位于北海的一个导管架式海洋平台为原型［7］，该平台主要结构参数见表 2，总高度 123.14 m，水深97.38 m。平台结构的初始有限元模型以每一根自然杆件为一个单元进行划分，其节点编号和单元编号如图2和图3所示，共有56个节点和132个梁单元。结构底部固定在海床上，平台甲板及上部结构的质量以集中质量的形式平均分配在顶部的四个节点上。所有单元的材料弹性模量取2.07×105MPa，泊松比0.3，质量密度为7 800 kg/m3。初始有限元模型为后续的模态应变能法损伤检测提供了单元划分，及其所需要的单元贡献矩阵和整体刚度矩阵。

图2 初始有限元模型及其节点号Fig.2 Initial finite element model and its node number

图3 初始有限元模型及其单元号Fig.3 Initial finite element model and its element number

表2 平台主要结构参数Tab.2 Main structural parameters of the platform

2.2 基于温度梯度的平台有限元模型再建

以图1中温度变化最大的7月份曲线为依据对该平台模型进行再建模，因为钢材的弹性模量随温度变化比较小，为了尽量少的改变初始模型同时又能较好的反应温度梯度对钢材弹性模量的影响，将海水在竖直方向上每隔5℃划分一个温度层。由表1可见，温度升高5℃钢材的弹性模量大约降低0.2%，在计算中已经能够满足精度要求。将平台有限元模型在温度分层处设置附加节点，这样按温度梯度划分一根杆件由于可能处于多个水温层而被划分为多个单元，如图4所示，附加节点编号从57开始，共新增了48个节点。再建的模型是接下来验证温度梯度对平台模态应变能法损伤检测影响的基础，算法所需的模态频率和模态振型都是通过该模型计算得到，为了和初始模型节点相对应，这里得到的模态振型只提取前56个节点的振型数据。再建的模型就可以根据温度层划分模拟温度梯度，即将各温度层中单元的弹性模量按照表1中对应的温度取值，以下称为加上温度梯度模型。加温度梯度和不加温度梯度模型的模态频率对比见表3，这里不加温度梯度是指该模型所有单元的弹性模量都取为2.07×105MPa，即0℃对应的取值。模型再建之后，为了便于后续研究，对不同类型构件进行了结构冗余度分析，分别计算了第四层的一个桩腿、斜撑和水平撑(图4局部放大所示)在损伤50%及100%的情况下结构模态频率的变化率，见表4。可见水平撑的损伤造成的前2阶频率变化之和最小，其结构冗余度最大，斜撑次之，桩腿最小。

图4 按温度梯度划分的平台有限元模型Fig.4 Finite element model of the platform divided by temperature gradient distribution

表3 温度梯度对模态频率的影响Tab.3 The influence of temperature gradient on modal frequencies

表4 不同类型杆件的结构冗余度分析Tab.4 Structure redundancy analysis for different types of components

2.3 温度梯度对平台模态应变能法损伤检测的影响分析

导管架式海洋平台第3阶模态通常为Z向扭转，在实测中不易测量，且模型修正困难［8］，所以在利用模态应变能法进行损伤检测时，模态阶数一般取前2阶弯曲模态(X、Y向)，即nm=2。这里只研究单一杆件损伤的情况，即nd=1。以杆件材料弹性模量的折减来体现损伤，即将某一杆件所有单元在当前温度下的材料弹性模量乘以(1-损伤百分比)，作为损伤杆件。首先利用再建的模型进行损伤前后结构的整体刚度矩阵和整体质量矩阵的特征值分解得到模态频率和模态振型(保留前56个节点的振型数据)，再结合由初始有限元模型得到的单元贡献矩阵和整体刚度矩阵，分别计算不同损伤工况下加上温度梯度和不加温度梯度损伤检测的结果，找出温度梯度对平台模态应变能法损伤检测的影响规律。从图4可见，第四层温度变化最为显著，分别取该层的一个桩腿、斜撑和水平撑作为检测对象，该层损伤单元的编号见图4中的局部放大图。

2.3.1 温度梯度对损伤定位的影响

损伤定位取Zj=2作为损伤的阈值来判别是否发生损伤。损伤程度从0开始，按2%递增，直到满足Zj≥2。通过分别计算不加温度梯度和加上温度梯度不同构件所能定位的最小损伤程度来研究温度梯度对损伤定位指标Zj的影响，图5～图7分别表示第四层结构的一个桩腿、斜撑和水平撑的识别结果。以图5为例，图5(a)表示桩腿76号单元在不加温度梯度的情况下发生10%的损伤即可被定位出来，图5(b)表示加上温度梯度后该桩腿损伤程度要达到18%才能被定位出来。而且加上温度梯度后，结构冗余度最小的桩腿部位的损伤指标Zj变得较大，如图5(b)中标出的非损伤杆件(桩腿77、79等)，图6及图7中Zj较大的杆件编号与图5(b)相同，位置如图3所示都发生在桩腿部位。对于结构冗余度最大的水平撑，如图7所示，不加温度梯度的情况下损伤28%即能被定位出来，加上温度梯度损伤66%才能被定位出来。

可见，加上温度梯度后，各类构件均需要发生更大程度的损伤才能被定位出来，或者说温度梯度使模态应变能法损伤定位能力变弱。相对而言，对结构冗余度大的构件影响大，对结构冗余度小的构件影响小。具体的，对水平撑的影响最为严重，对斜撑的影响次之，对桩腿的影响最小。

2.3.2 温度梯度对损伤程度识别的影响

对于每一类构件，先分别计算了模型不加温度梯度和加温度梯度可定位的最小实际损伤程度及其识别值，在此基础上逐渐增大损伤程度直到完全损伤，计算了不同实际损伤情况下的识别值。识别过程通过编程实现，将杆件的损伤程度(以材料弹性模量的折减来表示)作为输入变量，损伤程度从0开始按2%递增，循环计算损伤识别值αj，直到满足Zj≥2，此时的αj值即为可识别的最小损伤程度。在此基础上继续按2%的比例增加损伤，循环计算到完全损伤为止，记录每一步识别得到的αj值，并将有代表性的损伤程度和识别值列于表5。例如对于第四层桩腿的损伤识别，未加温度梯度可定位最小损伤程度为10%，识别值为8.44%，加上温度梯度后可定位最小损伤程度为18%，识别值为1.06%;当损伤程度增大到70%时，未加温度梯度识别值为63.04%，加上温度梯度识别值为60.62%。可见，不加温度梯度识别出来的损伤程度与真实值比较接近，加上温度梯度后识别的损伤程度要小于不加温度梯度时的识别值，或者说加上温度梯度会湮没掉一部分损伤程度，使识别精度降低。但是随着损伤程度的增加，温度梯度湮没掉的损伤程度越来越小，相反的，损伤越小湮没越多。以第四层三种构件为例，计算了在可定位的损伤程度范围内，由于温度梯度湮没掉的识别损伤程度随实际损伤程度的变化规律，见图8～图10。如图8所示，桩腿在损伤20% ～50%的情况下，温度梯度湮没掉的损伤程度为14% ～6%，而图10所示水平撑在损伤70% ～90%的情况下，温度梯度湮没掉的损伤程度为45% ～8%。可见，在可定位的损伤程度范围内，结构冗余度越大的构件，温度梯度湮没掉的损伤程度越大。

图5 桩腿76的损伤位置识别Fig.5 Damage location for pile leg 76

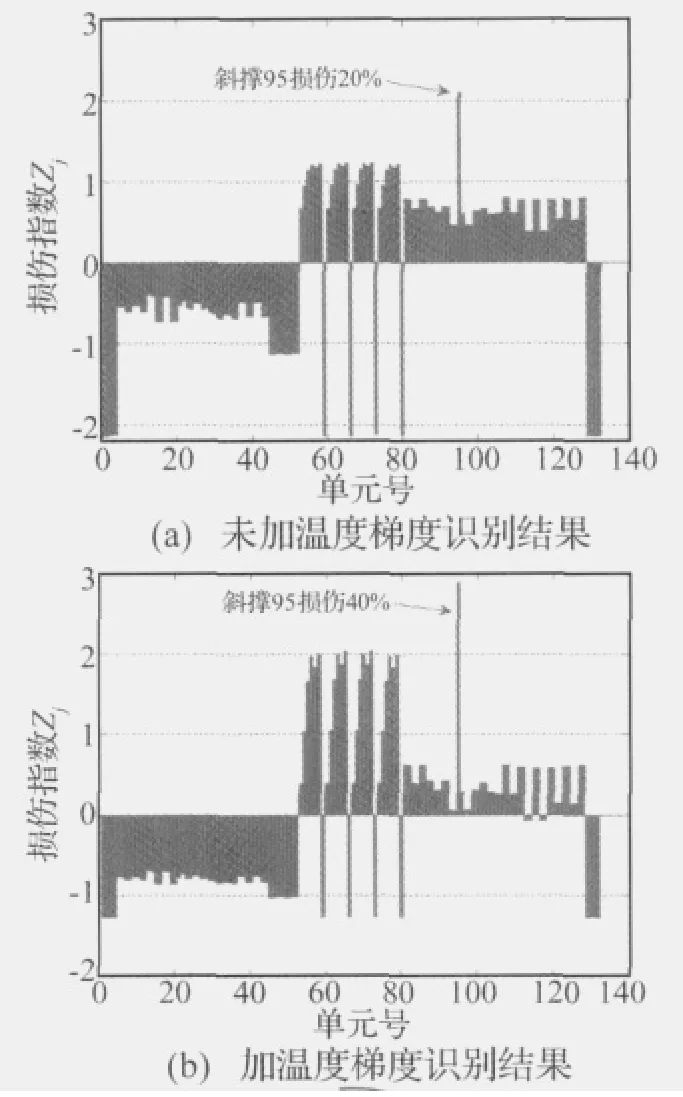
图6 斜撑95的损伤位置识别Fig.6 Damage location for slanted brace 95

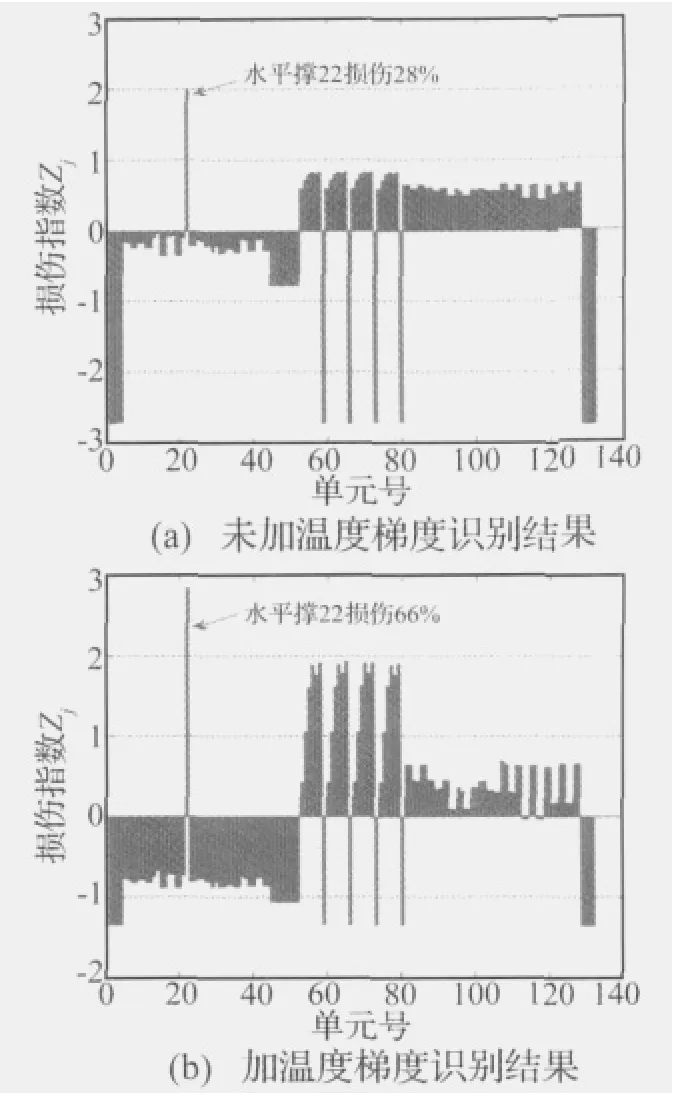
图7 水平撑22的损伤位置识别Fig.7 Damage location for horizontal brace 22

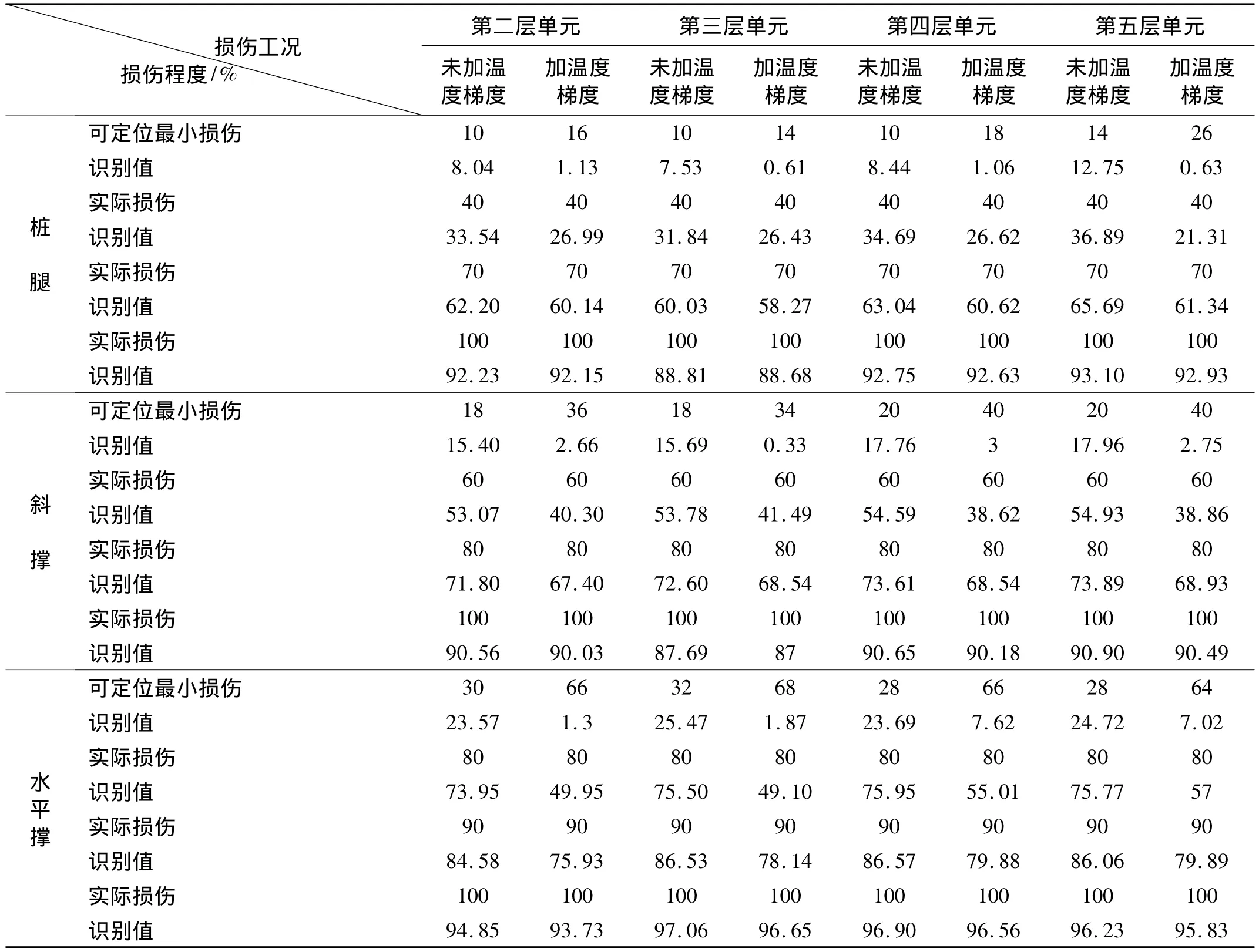
表5 各类构件的损伤程度识别结果Tab.5 Identification results of damage extent for different components

图8 温度梯度对桩腿损伤程度识别的影响Fig.8 The influence of temperature gradient on identification of damage extent for pile leg

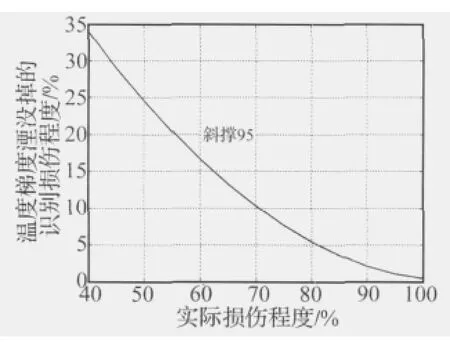
图9 温度梯度对斜撑损伤程度识别的影响Fig.9 The influence of temperature gradient on identification of damage extent for slanted bracing

图10 温度梯度对水平撑损伤程度识别的影响Fig.10 The influence of temperature gradient on identification of damage extent for horizontal bracing

3 结论

本文基于温度梯度的结构分层建模方法，研究了海水温度梯度现象对模态应变能法损伤检测的影响。通过对一个导管架式海洋平台模型进行数值分析，得到以下结论:

(1)以温度与钢材弹性模量的关系为基础，进行了海洋平台在海水温度梯度下的有限元模型再建，建立了一种海洋平台结构整体损伤检测受海水温度梯度影响的分析方法。

(2)加上温度梯度影响后，会使模态应变能法损伤定位能力变弱，对结构冗余度越大的杆件影响越大。具体来讲，对水平撑的影响最大，对斜撑的影响次之，对桩腿的影响最小。

(3)在可定位的损伤程度范围内，温度梯度会湮没掉一部分损伤程度，使模态应变能法损伤程度识别精度降低，且结构冗余度越大的构件湮没掉的损伤程度越大。但随着杆件损伤程度的增大，影响越来越小。

［1］杨和振，李华军，黄维平.基于振动测试的海洋平台结构无损检测［J］.振动工程学报，2003，16(4):480-484.

［2］孙 君，李爱群，丁幼亮，等.润扬大桥悬索桥模态频率—温度的季节相关性研究及其应用［J］.工程力学，2009，26(9):50-55.

［3］樊可清，倪一清，高赞明.大跨度桥梁模态频率识别中的温度影响研究［J］.中国公路学报，2006，19(2):67-73.

［4］卡缅科维奇，莫 宁.海洋物理学(第1卷)［M］.沈积均，杜碧兰，杨华庭译.北京:海洋出版社，1984.

［5］王文彬，林忠钦，严隽琪，等.机械设计手册(第1卷)［M］.北京:机械工业出版社，2004.

［6］ Kim J T，Stubbs N.Improved damage identification method based on modal information［J］.Journal of Sound and Vibration，2002，252(2):223-238.

［7］ Shi X，Matsui T，Mizuno K，et al.Damage detection in offshore jacket platforms based on partial measurement［J］.Journal of Structural and Construction Engineering， AIJ，2005，(591):169-177.

［8］刘爱霞，石 湘.一种海洋平台广义模型修正方法的研究［J］.振动与冲击，2007，26(1):3-6.