建筑结构鲁棒分散控制方法研究

蒋 扬，周星德，王 玉，刘谦敏，姜冬菊

(河海大学 力学与材料学院，南京 210098)

振动主动控制系统多采用集中控制策略［1-3］，需要同时测量尽可能多的系统信号，进而计算出所有作动器的控制力进行振动控制。倘若某几个控制器或传感器失效，则可能使控制系统瘫痪，且控制系统设计复杂、可靠性差。基于局部信息反馈的分散控制策略，具有设计简单且可靠性高等特点，已经成为目前研究的热点之一［4］。由于分散控制采用系统局部信号反馈的控制方法，少数作动器的失效并不会致使整个系统的控制失败，更适于实际应用。文献［5］对基于最优控制策略的分散控制方法进行了初步的研究;文献［6］通过把结构分成多个子系统，每个子系统采用不同的控制策略的方式，对自适应模糊分散控制进行了研究，控制效果很好。

本文主要研究基于鲁棒控制理论的鲁棒分散控制策略，目前分散控制作动器的控制力仅采用建筑物相邻两层的测量信号进行控制，由于采用的系统信息较少，虽然也能对建筑物的振动响应进行控制，但控制效果一般［7-10］。如果要使系统具有较好的控制效果，就必须为作动器提供尽可能多的系统反馈信息。因此，在信息采用上，本文选择建筑物相邻四层的测量信息，进而对其进行鲁棒分散控制，既保证了控制系统简单可靠的优点，又增加了作动器控制力所采用的系统信息，为同等环境下提高系统的控制效果提供了保证。最后，对十层建筑物进行了仿真分析。

1 鲁棒控制

含比例阻尼的n个自由度的建筑结构在地震作用w(t)下的运动方程为:

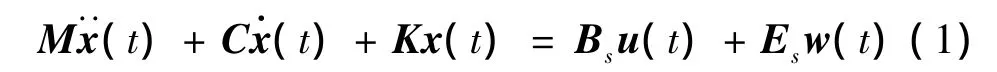
式中，x(t)∈Rn×1是建筑物的相对位移向量;M，C，K∈Rn×n分别是质量矩阵，阻尼矩阵和刚度矩阵;u(t)∈Rm×1是作动器控制力向量;Bs∈Rn×m为作动器定位矩阵，m为作动器数目;Es∈Rn×1为地震激励定位矩阵。w(t)为地面水平加速度时程曲线(t)，其定位矩阵Es为 -M{1}n×1。

定义状态变量:

则式(1)可以表示为如下状态方程:

式中，

其中，In×n为n×n维单位矩阵;0n×m，0n×p，0n×1分别代表n×n维，n×m维，n×1维零矩阵。

令振动主动控制系统的控制输出方程为:

式中，Y(t)∈Rq×1为控制输出向量;C∈Rq×2n和D∈Rq×m均为系统控制输出系数矩阵;q为控制输出变量个数。假设控制系统为状态反馈控制系统，即作动器控制力U(t)由方程U(t)=GZ(t)决定，G∈Rp×2n为控制增益矩阵。把方程U(t)=GZ(t)代入方程(3)、方程(4)，可得闭环系统的状态方程:

式中，

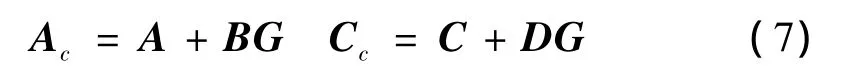
设离散周期为T，对系统状态方程进行离散化得:

式中，下标“d”表示相对应的离散系统。由于离散状态反馈系统中的控制力Ud(k)可以表示为Ud(k)=GdZ(k)。因此，离散闭环系统中的Adc和Cdc的表达式为:

设HZW是由输入w(t)到输出Y(t)的传递函数:

变量μ满足如下关系:

即变量μ为离散闭环系统传递函数HZW无穷范数的上确界。

由状态反馈控制系统鲁棒控制理论［11］可知，离散系统的鲁棒控制问题可以转化成在线性矩阵不等式约束条件下的凸优化问题，即求变量矩阵Fd和Θd，使其满足以下条件:

(1)Minimize μ

(2)使矩阵变量Fd和Θd满足如下不等式:

式中，Θd为2n×2n维对称正定矩阵，Fd为p×2n维矩阵，且满足关系:Fd=GdΘd;符号‘*’表示矩阵中相应的对称块。当上述凸优问题有解，即存在满足上式不等式约束条件的变量矩阵Fd，Θd，则增益矩阵Gd为:

2 鲁棒分散控制

根据线性状态反馈控制律U(t)=GZ(t)可知，当增益矩阵Gd1被应用时，第i层作动器控制力ui只跟第i层位移和速度有关;而当增益矩阵类型Gd2被应用时，第i层作动器控制力ui跟第i层及与之相邻两层(上下各一层)的位移与速度有关;以此类推，可根据不同需要，对任意系统增益矩阵Gd进行相应的定位约束。

同理，要得到满足定位约束条件的增益矩阵Gd1，需对变量矩阵Fd1和Θd1进行相应的定位约束。

3 仿真分析

图1 含10个作动器的10层框架Fig.1 The 10-storey frame structure

以10层框架建筑结构为研究对象进行鲁棒分散控制仿真分析，基于地震波的采样周期为0.02 s，所以采用 0.02 s作为系统的离散周期。如图1所示，在建筑结构的每一层都安置一个假设为理想作动器。通过三种不同定位约束的控制增益矩阵GdⅠ，GdⅡ，GdⅢ分别对建筑物进行了鲁棒分散控制仿真研究。GdⅠ，代表方法1，是基于建筑物相邻两层测量信号的鲁棒分散控制策略，即第i层作动器的控制力只跟第i层及与其相邻两层(上下各一层)的位移与速度有关;GdⅡ，代表方法2，是基于建筑物相邻四层测量信号的鲁棒分散控制策略，即第i层作动器的控制力只跟第i层及相邻四层(上下各二层)的位移与速度有关;GdⅢ，代表方法3，是指鲁棒集中控制策略，即第i个作动器的控制力跟结构各层的位移与速度都有关，取决于系统的全局测量信息。仿真分析过程以各楼层相对地面的位移与速度为控制输出，即Cd为20×20维单位矩阵，Dd为相应的零矩阵。假设系统初始处于静止状态，外部激励为水平方向的地震荷载，选择elcentro波作为水平方向激励，结构阻尼比为0.02;各楼层的质量均为3.2×103kg，刚度为 4.3 × 106N/m。控制增益矩阵GdⅠ，GdⅡ，GdⅢ的值，可以通过相应的凸优化问题求解，并对建筑物进行振动控制。鲁棒分散控制的仿真结果如表1所示。

从表1中可以看出，方法2与方法3的控制效果明显优于方法1。方法1能使建筑物楼层位移响应的峰值减少40～50%左右，而方法2与方法3的控制效果基本相当，能使建筑物楼层位移响应的峰值减少90～98%左右。由此可知，鲁棒分散控制的效果依赖于系统测量信息量的多少，当各作动器采用的系统信息量较少时，其控制效果一般;相反，当各作动器所需的系统信息量较多时，往往能达到较好的控制效果。如表1所示，方法1只能减少建筑物各楼层不到50%的位移响应峰值。而方法2的控制效果明显优于方法1，能够减少各楼层90%以上的位移响应峰值。但是，鲁棒分散控制的控制效果并不是随着作动器所需系统测量信息数量的增加而无限增加，如方法2与方法3的控制效果基本相当。甚至在建筑物的第3层，方法2对建筑物位移响应峰值的减少量反而大于方法3约2.5%。因此，对于建筑结构的鲁棒分散控制，在同等条件下，应该存在一个最优增益矩阵的定位约束类型，即作动器控制力所需的系统测量信息量存在一个最优值，使得控制系统能够用较少的测量信息达到最优的控制效果。

表1 建筑物鲁棒分散控制结果Tab.1 Control result of the robust decentralized control method

同时，以结构第10层的控制效果图为例，以便对鲁棒分散控制的控制效果认识更直观。方法1，方法2，方法3的控制效果分别见图2，图3，图4，其中，虚线表示未控制时的位移时程曲线，实线为控制后的位移时程曲线。方法2的第10层作动器的控制力时程曲线如图5所示。从图中也可以清楚的看出，基于建筑物相邻四层测量信号的鲁棒分散控制的控制效果与鲁棒集中控制的控制效果基本相当，且明显好于基于相邻两层信号的鲁棒分散控制效果。

此外，在研究过程中也出现了一些现象:① 当控制系统中只采用四个，五个等少量作动器进行分散控制时，建筑物位移响应几乎得不到有效控制，甚至比未控时的响应还要大;② 当控制系统采用三个及更少的作动器进行控制时，采用基于建筑物局部测量信息反馈的鲁棒分散控制策略，在MATLAB仿真过程中，其相应的凸优化问题都会出现无解的情况。目前，作动器个数对鲁棒分散控制控制效果的具体影响及原因尚不明确，需进一步深入研究，这也成为笔者未来的研究重点。

4 结论

对于建筑结构在地震激励下的振动控制，传统鲁棒集中控制策略的系统复杂且可靠性相对较低，当其中少数作动器的失效就可能导致整个控制系统控制失败。因此，具有系统简单可靠性高等优点的鲁棒分散控制策略，在保证控制效果的情况下，可以一定程度上弥补鲁棒集中控制策略的不足。本文通过对10层建筑结构进行仿真分析，对基于建筑物相邻四层测量信号的鲁棒分散控制方法进行了初步研究。结果表明，该方法有效且控制效果较好。

［1］Soong T T.Active structural control:Theory and practice［M］.England:Wiley，Harlow，Essex，1990.

［2］ Yao J T P.Concept of structural control［J］.Journal of Structural Division(ASCE)，1972，98(7):1567-1574.

［3］Chu S Y，Soon T T，Rein A M.Active，hybrid，semi-active structural control:design，implementation，handbook［M］.Hoboken＆ NJ:Wiley，2005.

［4］Siljak D D.Decentralized control of complex systems［M］.Boston:Academic Press，1991.

［5］Li H G，Li Y，Li G.Decentralized control of structures under earthquakes ［J］.China Civil Engineering Journal，2009，41(9):27-33.

［6］Wang J，Li H，Li Y，et al.Nonlinear decentralized control of seismically excited civil structures［C］//.Active and passive smart structures and integrated systems，California:Mehdi A，Mehrdad N，Ghasemi N，2009:72882E-72882E-11.

［7］Wang Y，Wireless sensing and decentralized control for civil structures:theory and implementation［D］.California:Thesis， DepartmentofCiviland Engineering，Stanford University，2007.

［8］Boyd S，Feron E，Balakrishnan V.Linear matrix inequalities in system and control theory［M］. Philadelphia:SIAM，1994.

［9］ Borrelli，Tamás B，Gary J，et al.Hybrid decentralized control of large scale systems［C］.Zurich:8th International Workshop on Hybrid Systems:Computation and Control，2005:168-183.

［10］徐 洋，姜洪洲，叶正茂，等.H∞ 控制在AMD Benchmark结构主动控制中的应用研究［J］.振动与冲击，2005，24(5):14-17.

［11］Zhou K，Doyle J C，Glover K.Robust and optimal control［M］.Englewood＆ NJ:Prentice-Hall，1996.

附录1:方法2的控制器结构参数(增益矩阵GdⅡ=P×105)