班轮公司集装箱空箱在途库存控制研究
宋若辰,赵一飞
(1.上海交通大学船舶海洋与建筑工程学院,上海 200240;2.上海交通大学安泰经济与管理学院,上海 200240)
班轮公司集装箱空箱在途库存控制研究
宋若辰1,赵一飞2
(1.上海交通大学船舶海洋与建筑工程学院,上海 200240;2.上海交通大学安泰经济与管理学院,上海 200240)
为解决集装箱管理问题,在合理分析集装箱空箱在途库存成本构成的基础上,构建空箱在途库存成本优化模型,并结合算例,以空箱在途库存成本最小为优化目标,给出班轮公司最佳调运方案,同时验证该模型的可行性和有效性。
空箱;在途库存;成本控制;整数规划
0 引言
随着世界经济和国际贸易的发展,集装箱化已经成为现代化运输的重要标志之一。集装箱班轮运输体现了明显的规模经济效应,所以成本控制是班轮公司营运是否成功的关键因素所在,降低集装箱管理成本是班轮公司集装箱管理部门与学术界共同探索的课题。
当前若干针对集装箱管理的研究均集中于空箱调运问题上,其核心是解决集装箱需求与供给间的不平衡,控制和决策空箱从供应地到需求地的流动。一般可分为内陆运输和海洋运输两类。陆运方面,Kai Homberg,等[1]对铁路集装箱空箱调运进行了研究,建立了多货种网络流模型;刘大镕,等[2]研究了单箱种集装箱陆上调运模型,以公路和铁路为主的调运优化问题的研究日益完善。海运方面,大多数研究借鉴陆运但仍不够完善。周红梅,等[3]建立了海上集装箱空箱调运优化静态模型;施欣[4]采用Games软件包对构造的海运集装箱空箱调运系统模型进行模拟;丁敏,等[5]应用启发式算法对集装箱空箱调运进行优化研究。除此之外,近年来国内外学者和相关研究人员也逐渐开展对空箱调运的多式联运研究,S.T.Choong,等[6]建立了以美国5 大湖区为实际调运背景的空箱多式联运调运整数规划模型,考虑了公路、铁路和水运3种运输情况;丁菲[7]分别建立了陆运、海运和多式联运条件下空箱调运的静态和动态模型。
但是,研究大多局限于空箱调运成本方面,忽略了由于空箱调运这一动作产生的空箱在途库存成本,忽视资金占用的时间价值,从而低估了班轮公司进行集装箱管理的成本,这不利于对其进行有效合理的控制。笔者在本文中建立班轮公司集装箱空箱在途库存成本控制模型,通过降低空箱在途库存成本,提高集装箱班轮公司运营效益,弥补现有研究不足。
1 空箱在途库存成本
通过对集装箱运输及管理过程的理解,描述班轮公司空箱流转过程如图1。
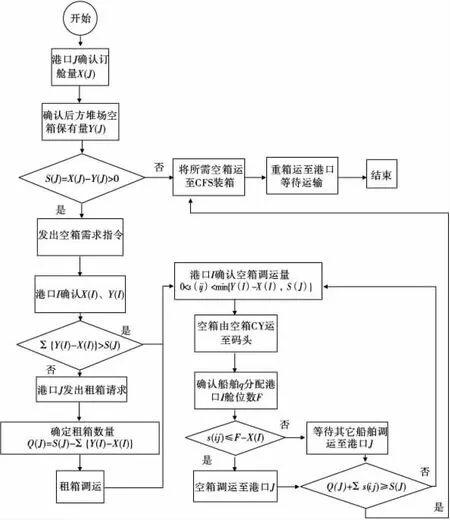
图1 班轮公司集装箱空箱流转过程Fig.1 Liner operators’circulation process of empty containers
1.1 物理空箱与财务空箱
由图1可看出,集装箱由空箱CY调运至CFS时属于物理形态意义上的空箱,运送过程中必然会产生空箱成本。但由于货主提重箱及归还空箱的时间具有很大不确定性,导致对此期间所产生的成本费用进行单独衡量非常困难。在实际操作过程中,班轮公司已将这部分成本分摊到运费中,无论货主是否提前取箱或还箱,不会造成班轮公司额外成本的产生,不改变(或仅增加)原有收益。故在此期间集装箱虽然处于空置这一物理形态,但从财务的角度上来看,并不会导致空箱资金占用成本的增加,即财务空箱是指在进行成本费用计算时有实际意义的空箱,这便产生物理空箱与财务空箱在概念及使用上的差别。
在对空箱在途库存成本进行研究时,研究对象仅指财务空箱,认为物理空箱流转是非有效流转,不需计算运输物理空箱而导致的成本费用。
结合财务空箱概念,笔者将空箱有效流转过程分为3种情况:
1)空箱在枢纽港之间的海上运输;
2)空箱在枢纽港与支线港之间的海上运输;
3)空箱在CY与港口码头之间的内陆运输。
1.2 空箱在途库存成本定义及构成
在途库存是指尚未到达目的地,正处于运输状态或等待运输状态而储备在运输工具中的库存,其大小取决于需求和生产-配送周期。迄今,有关在途库存的研究的文献不多,并且对其构成尚存在多家争论[8],对于空箱在途库存成本定义及构成更无明确解释及划分。
笔者将空箱在途库存成本定义为由空箱需求节点下达空箱需求指令后,通过各种运输工具,将空箱由供给节点运至需求节点这一过程所产生的库存持有成本。成本构成主要分为以下4部分:空箱在途库存资金成本、在途保险成本、在途风险成本和机会成本。
1)空箱在途库存资金成本。主要指班轮公司自有或者租用空箱在流转过程中所占用的资金成本,与所需调运空箱量及其处于在途库存状态的时间紧密相关。
2)空箱在途保险成本。空箱在途保险成本是主要组成部分之一,当空箱处于在途库存状态时有可能发生跌落等事故,因此很多班轮公司都会为集装箱办理保险,且所办理险种一般为一切险。
3)空箱在途风险成本。反映了除保险公司承担的责任之外,班轮公司仍需负责的其它损失及费用。通常包括集装箱内在缺陷和特性、延迟、工人罢工、战争、核武器威胁、武装集团扣押等所引起的损失和费用。
4)机会成本。班轮公司在正常营运过程中一般首先会保证重箱的运输需求,之后再利用剩余舱位满足空箱调运需求,但有时由于空箱资源的极度不平衡,会导致班轮公司需要占用重箱运输箱位来安排空箱的调运。由于空箱在途运输而产生重箱额外库存成本为空箱在途库存导致的间接成本,即为机会成本。
2 空箱在途库存成本控制模型
2.1 模型假设
研究空箱在途库存的目的是寻求需求与成本之间的平衡,在此做出如下假设条件:①仅考虑自有箱在各枢纽港之间的海上调度,以及租用空箱的内陆运输,暂不考虑自有空箱的支线运输以及内陆运输;②已知各个港口(或场站)初始空箱保有量;③所有集装箱都具有相同尺寸,即不考虑箱型约束,均为20尺箱;④不考虑集装箱转运和往复运输情况,即空箱是由供给港直接送达到需求港;⑤保证重箱运输需求能够及时得到满足,暂不考虑机会成本;⑥航班航线固定不变,船舶到达港口时立刻卸箱、卸货,从而获得可用空箱;⑦首先考虑进行港口间空箱调运,当自有空箱供给量无法满足需求量时再考虑租箱。
2.2 参数与变量
2.2.1 基本参数
N 为港口节点集合,i,j=1,2,…,N,i,j∈ N;
k为模型周期数,k=1,2,…,K ,根据实际操作和简化问题的客观需要,在模型中假设其为离散;
q 为港口挂靠船舶数量,q=1,2,…,Q;
2.2.2 确定性变量
j
Uj表示j港口的最大存储能力;
cij_cap,cij_ins,cij_risk分别表示单位时间内单位空箱在途库存资金占用成本、在途保险成本及在途风险成本;
tj表示在j港口将租用的单位空箱由空箱堆场调运至码头的时间;
c'j表示在j港口的租箱费率。
2.2.3 决策性变量
2.3 模型建立
2.3.1 目标函数

根据参数设置,可以定义一个班轮公司自有集装箱空箱在途库存控制系统。式中:cg表示空箱单位价值;α表示集装箱预计净残值率;Ts表示单位自有集装箱预计使用年限;cb表示单位集装箱保险金额;φb表示集装箱保险费率;Tb表示集装箱投保年限;cf表示由于发生战争、工人罢工等事件造成集装箱损失;ηij表示由i港到j港的航线上发生战争、工人罢工等事件概率。
2.3.2 约束条件

3 算例分析
假设系统内港口数N=4,船舶数q=2,航线上两条船舶对开,在满足重箱运输需求后可运载空箱数量上限分别为60 TEU和50 TEU。阶段数(周期数)k=4,每一个班期开始前安排空箱调运计划。各港口初始空箱保有量X0分别为300,350,550,250 TEU,考虑租箱,认为港口存储能力完全能满足港口空箱保有量所需。结合集装箱运输市场相关定价,令 cij_cap=4.65元,cij_ins=4.6元。由于空箱在途风险的发生一般为小概率事件,故在此假设cij_risk=0。具体运输路径如图2。
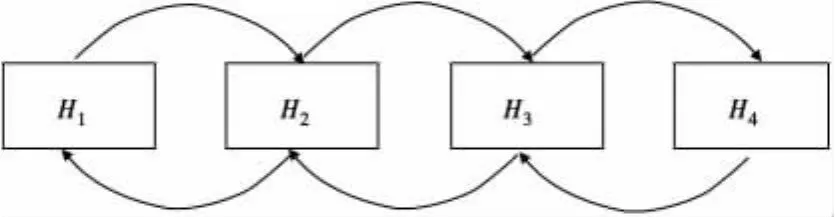
图2 某班轮公司集装箱运输航线Fig.2 A liner operator’s container transport routes


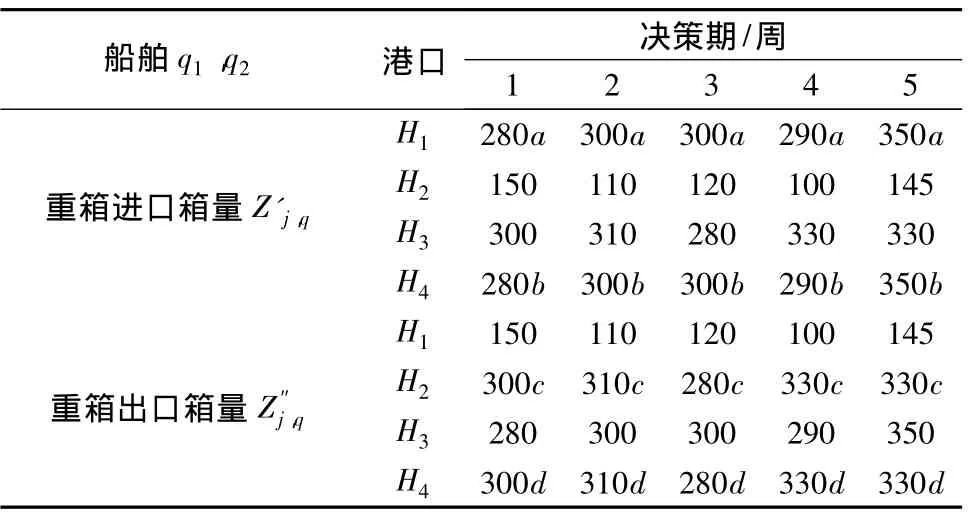
表1 各港口通过某条船舶重箱进出口量Table 1 Full containers’volume of import and export each port through a liner /TEU

表2 港口之间运输时间Table 2 Transport time between ports

表3 各港租箱所需运输时间及费率Table 3 Transport time and rates of renting containers
根据港口初始空箱保有量及重箱进出口箱量,不考虑成本及调运时间,以必须满足各港空箱需求为前提进行空箱调运安排,最终求得空箱在途库存成本为28 704.75元,调运方案如表4。

表4 空箱调运方案Table 4 Scheme of empty containers allocation /TEU
若构建空箱在途库存成本最小化模型,k=1时,根据各港口初始空箱保有量及实际重箱进出口箱量,有:

同理,令k=2,3,4继续求解,最终求得目标函数值为25 819.35,即空箱在途库存总成本最小为25 819.35元,最优空箱调运方案如表5。

表5 最优空箱调运方案Table 5 Optimal scheme of empty containers allocation/TEU
由表5可知,除了第1、4阶段需在H3和H2港口分别租用30,45个空箱以外,其它阶段通过空箱调运即可满足空箱需求。4个阶段结束时空箱调运总量较优化前减少92 TEU,租箱量增加15 TEU,总空箱在途库存成本节约2 885.4元。
根据计算可知,笔者所建的空箱在途库存整数规划模型可解出班轮公司在各个阶段最优空箱调运方案,并且使得规划期内总空箱在途库存成本费用最低。
4 结语
从财务成本角度对空箱及空箱在途库存进行分析与定义,并针对多个港口之间的空箱调度问题建立空箱在途库存成本控制模型,成功的进行了算例分析与求解,证明了模型的可行性。这种方法在研究空箱调运方案等问题上十分方便,可快速有效地进行空箱调运流量调控。由于现实中各周期空箱需求和供给具备不确定性,并且这种不确定性随着时间跨度延长而增大,故本方法更适用于短期调运方案规划。
[1]Homberg K,Joborn M,Lundgren T.Improved empty freight car distribution[J].Transportation Science,1998,31(2):163-173.
[2] 刘大镕,贺斌,蒋良奎,等.随机(单箱种)陆上空箱调运模型[J].上海海运学院学报,2000,21(3):8-18.
Liu Darong,He bin,Jiang Liangkui,et al.Random model of overland empty container distribution(single type)[J].Journal of Shanghai Maritime University,2000,21(3):8-18.
[3]周红梅,方芳.航运集装箱空箱调运优化模型的研究[J].武汉理工大学学报,2000,27(3):384-387.
Zhou Hongmei,Fang Fang.Research on the optimization model of empty container distribution[J].Journal of Wuhan University of Technology,2000,27(3):384-387.
[4]施欣.集装箱海运空箱调运优化分析[J].系统工程理论与实践,2003,23(4):70-89.
Shi Xin.The optimization of sea-bound empty container distribution[J].Systems Engineering:Theory & Practice,2003,23(4):70-89.
[5]丁敏,孙文一,顾伟红.集装箱空箱调运的启发式算法优化研究[J].中国航海,2008,3(1):75-78.
Ding Min,Sun Wenyi,Gu Weihong.Research on the optimization of empty containers allocation based on heuristic algorithm [J].Navigation of China,2008,3(1):75-78.
[6]Choong S T,Cole M H,Kutanoglu E.Empty container management for intermodal transportation networks[J].Transportation Research:Part E,2002,38:424-438.
[7]丁菲.海运与多式联运下的集装箱空箱调运优化研究[D].上海:上海海事大学,2005.
[8]何芬,翁玉婷,张玲玲,等.库存成本的分解及结构[J].物流工程与管理,2010,32(11):35-36.
He Fen,Weng Yuting,Zhang Lingling,et al.The decomposition and composition of the inventory costs[J].Logistics Engineering and Management,2010,32(11):35-36.
Study on Liner Operators’Controlling of Empty Containers’In-Transit Inventory
Song Ruochen1,Zhao Yifei2
(1.School of Naval Architecture,Ocean & Civil Engineering,Shanghai Jiaotong University,Shanghai 200240,China;
2.Antai College of Economics& Management,Shanghai Jiaotong University,Shanghai 200240,China)
To solve the issue of container management,based on rational analysis concerning the cost composition of empty containers’in-transit inventory,an optimization model which aims to minimize the overall cost of empty containers’in-transit inventory is devised.Besides,a specific case is also taken into consideration,so as to provide the best distribution program for liner operators as well as verify the feasibility and efficiency of this model.
empty container;in-transit inventory;cost control;integer programming
U169.6
A
1674-0696(2012)04-0890-05
10.3969/j.issn.1674-0696.2012.04.37
2011-10-18;
2012-04-11
2010年度上海市政府决策咨询研究重大研究项目(2010-Z-66)
宋若辰(1987—),女,内蒙古赤峰人,硕士研究生,主要从事航运与物流管理方面的研究。E-mail:srcsjtu0902@126.com。

