基于缓解公交列车化现象的最小发车间隔研究
周嘉男,罗 霞,黄启乐,魏 强
(西南交通大学交通运输与物流学院,四川成都610031)
近年来我国城市公共交通建设取得较大进展,如何合理安排公交调度,使公交资源充分利用,是当前城市交通管理者面临的一项难题。当前公交列车化现象频发,导致道路服务水平降低,车辆运营成本增加,乘客服务水平下降[1]。发车间隔的确定对缓解公交列车化现象具有指导意义。
文献[2-7]阐述了基于客流断面、遗传算法等方法来获得最佳发车间隔。但这些方法均假设公交车全程在正常状态下运行,所得出的计算结果并不能有效降低实际运行过程中公交列车化现象出现概率。笔者针对这一问题,从考虑如何确定发车间隔的约束下限的角度出发,来探讨对公交列车化现象的缓解方法。通过分析公交列车化现象的产生原因,并以现有发车间隔模型为基础(引入最小发车间隔概念,并作为约束条件之一),以公交运营成本最小、乘客利益最大为目标函数,建立基于缓解公交列车化现象的最小发车间隔计算模型,以说明在公交列车化现象得到缓解的前提下,达到公交运营成本和乘客出行成本之和最小时,最小发车间隔的取值,并以成都市81路公交车为例进行分析。
1 公交列车化问题分析
1.1 问题描述
公交列车化现象是指特定公交线路在全线运行过程中发生的列车化现象。具体表现为在某一特定的公交线路上,在各班次车辆按调度计划发车并遵守行车路线的情况下,由于道路运行条件等非人为因素所导致的相邻班次公交车首尾相接,或以远小于规定发车间隔的时间为车头时距跟驰运行的现象。
假设公交车均按固定路线行驶,公交车流为限制超车的单列车流,公交车车头时距符合移位负指数分布[8]。评估一般条件下是否产生公交列车化现象的条件是:在车辆运行该线路平均站距所需时间内,其相邻班次车头时距远小于公交车规定发车间隔的出现概率是否较大。车头时距分布函数为:
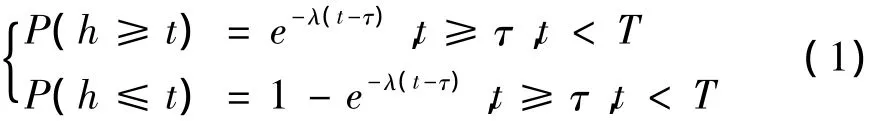
式中:λ为公交车到达强度,veh/min;h为相邻班次车辆实际车头时距,min;τ为理想条件下相邻班次车辆车头时距最小间隔,通常取2 s;t为判断限值,是一个远小于公交车规定发车间隔的值,min;T为发车间隔,min。
若P(h≤t)→1,则认为该线路相邻班次公交车存在公交列车化现象。
1.2 原因分析
公交列车化现象是由于乘客行为、道路交通条件、调度行为等一系列相关因素相互作用形成的结果,产生原因比较复杂。笔者从乘客、道路交通条件和调度方法等3个角度分析其产生原因。
1.2.1 乘 客
假设某线路公交车在各运行区间内平均速度相同,发车间隔不变,某公交车站在相邻两辆公交车依次进站的时间间隔内,乘客规模为w且在一定时间内不变,则公交车在该站停靠延误时间t停为:

式中:w为乘客候车规模,取上、下车人数中的最大值,人;t上下为乘客上下车平均时间,s/人;t固定为其他固定延误(如车辆进出站时间等),s。
若t停大于下一辆公交车到达该车站所需时间,则认定有较大可能在该车站处发生列车化现象。因此,当乘客候车规模越大时,该线路越易发生列车化现象。另外,当相邻车站乘客候车规模差异较大时,由于下一班车辆在上一车站处停靠站延误时间较小,导致下一辆公交车到达该车站所需时间减少,更易产生公交列车化现象。
1.2.2 道路交通条件
在道路几何、管理控制和交通流等条件的综合作用下,对常规公交运行质量影响的直接表现是,车辆在不同运行区间内平均运行速度不同。假设某线路公交车按固定线路并全程在公交专用道上行驶,用平均运行速度来表示综合条件对运行质量的影响,发车间隔不变,乘客规模不变,设两车起始间距为S,前、后车平均运行速度分别为和,且<那么t时间后两车间距ΔS为:

1.2.3 调度方法
对某条特定的公交线路,由于发车间隔能够进行人工调整,有别于乘客候车规模、区间平均运行速度等不可控的变量,公交公司可根据乘客候车规模和道路交通运行条件来确定发车间隔,使发车间隔同满足乘客需求相适应。
图1为成都市部分干线公交不同时期内的发车密度(注:此处高峰期间发车间隔为平均值,但发车间隔不能无限减小)。高峰期间主干路段交通流接近强制流且车辆运行速度较低,稍有影响即引起系统的不稳定,出现拥挤。在此条件下以较小的间隔发车,可能会由于前车的随机停车导致列车化现象发生。根据式(2),发车间隔至少应大于t停,才能有效避免在车站处发生列车化现象。当发车间隔越小时,越容易出现公交列车化现象。由于发车间隔的可操作性较强,因此对发车间隔的确定可以对公交列车化现象产生直接改善。
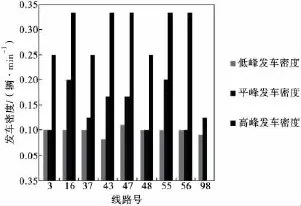
图1 成都市部分干线不同时期内发车密度Fig.1 Different headways densities during different periods on part of main routes in Chengdu
1.3 公交列车化现象的影响
1)道路服务水平。若某一公交专用道处发生公交列车化现象,由于车辆跟驰运行和交通波向后传递的原因,最直接的影响是考察路段交通密度迅速增大,导致道路服务水平降低。
2)车辆运营成本。公交列车化现象通常伴随较小发车间隔,意味着在相同时间内该线路要发出更多班次的车辆,每开出一班车存在固定和可变运输成本[9],故增加班次相当于增加了该线路的运营成本。由于此时存在一定量无效运营车辆(即由于发车间隔过短且在该时间间隔内没有足够乘客到达,导致后车的利用率降低),故该部分增加成本并非必要,应予以降低。
3)乘客。若某线路公交车配车数不变,公交列车化现象可能导致前后相邻两班次车辆间隔较大、但却同时存在后车车辆同下一班次车辆出现列车化的现象。这在部分公交车站产生同一班车辆的乘客候车规模较大甚至达到无法及时消散的状态,增加了车站的拥挤程度,使乘客对公交的满意度下降。
2 最小发车间隔
2.1 最小发车间隔内涵
发车间隔关系到乘客的直接利益和公交公司的运营效益。乘客希望发车间隔较短,这样候车时间较短且不会过度拥挤;公交公司希望发车间隔有一定长度,以提高满载率、公交车的有效利用率,降低运营成本以提高效益。
笔者在基于缓解公交列车化现象的前提下提出了最小发车间隔的概念。从公交公司效益角度讲,设定最小发车间隔应保证该线路公交车按此间隔发车的条件下,在中心城区路段不发生公交列车化现象,此时公交车的利用率提高,班次减少,运营成本降低;从乘客角度讲,该线路公交车按最小发车间隔进行发车时至少能满足该线路高峰期大部分车站的客流需求,确保服务水平同现状持平。若相邻两班次公交车从起始站出发的间隔时间T满足以下条件,则认为该发车间隔可以作为最小发车间隔Tmin。
2.1.1 公交公司效益的条件
1)满足车辆在中心城区路段公交车站处停靠时不出现列车化现象的条件。令全线路所有公交车站乘客候车规模平均值为,在连续的所有公交站处的最大停靠站延误时间为 t停max,发车间隔T ≥t停max,根据式(2),有

式中:w0max为高峰期全线各车站中单位时间内乘客候车规模最大值,人/min。
2)满足在中心城区路段运行时不出现列车化现象的条件。令全线路所有公交车站乘客候车规模平均值为,在连续wi>的所有公交站所包含的运行区间内,存在车头时距最小值hmin≥T,且此时车头间距s同hmin的比值s/hmin应不小于该运行区间道路临界速度vm。
2.1.2 乘客服务水平的条件
车辆在发车间隔内最大乘客候车规模为w0maxT,令ρ为确保乘客舒适度的实际载客数同最大载客数之比,C为车辆最大载客数,存在:

综合式(1)、式(2),最小发车间隔Tmin成立条件为:
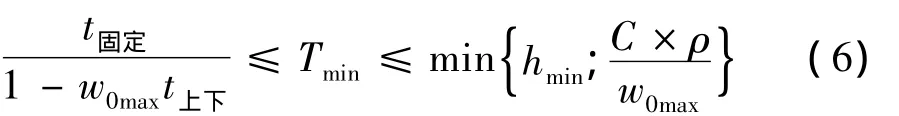
综上,在确定最小发车间隔时需要满足的两个基本条件是:公交车在全线运行过程中不出现列车化现象;乘客服务水平应在原有基础上提高,或尽量保持原有服务水平。但在实际情况下,缓解公交列车化现象并不是实现公交车调度的唯一目的。在确定公交车发车间隔时,其他已有的约束条件(如客流)同最小发车间隔约束条件相比同样重要。最小发车间隔这一变量是在已有的方法和思维方式基础上的延伸,并非从根本上对现有公交车调度方法进行改变。
2.2 最小发车间隔现实意义
2.2.1 道路服务水平
设置最小发车间隔后,车辆以离散的形式取代连续到达的形式进入考察路段,因此不存在跟驰运动及运动状态以交通波的形式向后传递的现象,故不会出现列车化现象,较高的道路服务水平将得到维持。
2.2.2 车辆运营成本
若相邻两班次车辆在到达该线路上乘客候车规模最大的车站所对应的运行区间或在此之前已发生列车化现象,那么当处于该运行状态的公交车经过该路段后,将面对乘客候车规模越来越小的情况,造成运力浪费,导致运营成本提高。设置最小发车间隔现实意义之一是降低该线路车辆运营成本。
2.2.3 乘 客
当Tmin=t停max时,会发生当前车刚出站时后车恰好进站这种理想运行状况(图2),确保了乘客的乘车需求始终能够得到满足。由于车辆在全线路段运行过程中存在最小车头时距hmin,因此“一直等不到车,但在下一班时同时有多辆车同时进站”的现象将得到缓解。

图2 最小发车间隔取下限值时车辆运行状况Fig.2 Vehicle operation conditions with lower limit value of minimum headways
3 模型的建立
3.1 建模思路
在设置最小发车间隔时,既要使公交企业运营成本最小,又要使乘客服务水平最大。为方便求解,将该问题转化为单目标优化问题。将乘客服务水平转换为乘客出行成本,因此,原问题目标函数为求公交企业运营成本同乘客出行成本之和的最小值,该问题的最终目的是需要求得最小发车间隔在目标函数取最小值时的结果。同时为确保不发生公交列车化现象,将对最小发车间隔的取值范围做出确定,作为约束条件,将运营成本和乘客出行成本均看作是最小发车间隔的函数。
由于最小发车间隔越小,平均周转时间内该线路车辆的配车数越多,故该线路配车数同最小发车间隔成反比例关系,得出公交企业运营成本同最小发车间隔成反比例关系;乘客的出行成本与乘客平均候车时间和车辆平均满载率(分别对应乘客候车成本和乘客乘车成本)有关,关于乘客候车成本,应考虑站台的乘客候车规模和平均候车时间;关于乘客乘车成本,应考虑车站处断面流量和车辆平均满载率。综合以上两点得出乘客出行成本同最小发车间隔成正比例关系。
确定运营成本、乘客出行成本同最小发车间隔的函数关系后,需要根据二者的侧重程度来分别确定其权重系数,相加得到目标函数。约束条件从以下角度考虑:车辆配车数上限、按乘客舒适度确定的车辆满载率上限、不出现列车化现象条件下的最小发车间隔取值范围等。
3.2 模型假设
1)特定时间段所有车辆都沿规定的路线运行且均在一条公交专用道上行驶;
2)同一线路上所有公交车具有相同的最大载客数量;
3)所有在车站候车的乘客在车辆到达时均上车,乘客上下车平均时间固定,车辆进站、出站时间固定;
4)同一线路所有车辆在特定时间段内发车间隔固定;
5)车辆运行速度只与道路交通条件、交通流状态有关,某特定运行区间、特定时间段内平均运行速度为恒定值;
6)所有车辆在任何情况下均不允许超车和越站;
7)同一线路不同票价之间不具有相关性;
8)同一线路所有车辆在特定时间段内均按最小发车间隔发车。
3.3 变量及符号说明
3.4 模型建立
3.4.1 公交公司运营成本
假设车辆均以最小发车间隔发车,得到运营成本关于最小发车间隔的函数为:

3.4.2 乘客出行成本
乘客出行成本包括候车成本和乘车成本两部分。
1)乘客候车成本。乘客候车成本与发车间隔内车站所有乘客平均候车时间有关。车站i在最小发车间隔内乘客的候车规模为:

在乘客候车规模很大的情况下,可将乘客平均候车时间简化为同一线路相邻两班次车辆到达时间间隔Tmin的一半。故所有车站乘客候车总时间为:

加入经验折算系数,得到乘客候车成本关于最小发车间隔的函数为:

2)乘客乘车成本。乘客乘车成本与车站处断面流量和平均满载率有关。所有车站在Tmin时间内单向断面平均流量为:

车辆在所有车站处平均满载率为:

加入经验折算系数,得到乘客乘车成本关于最小发车间隔的函数为:

将式(10)与式(13)相加,得到乘客出行成本关于最小发车间隔的函数:

3.4.3 确定目标函数
对公交公司运营成本和乘客出行成本分别赋权重α和β的值。将公交公司运营成本和乘客出行成本加权平均得到总成本关于最小发车间隔的函数,即:

3.4.4 确定约束条件
该模型约束条件如下:
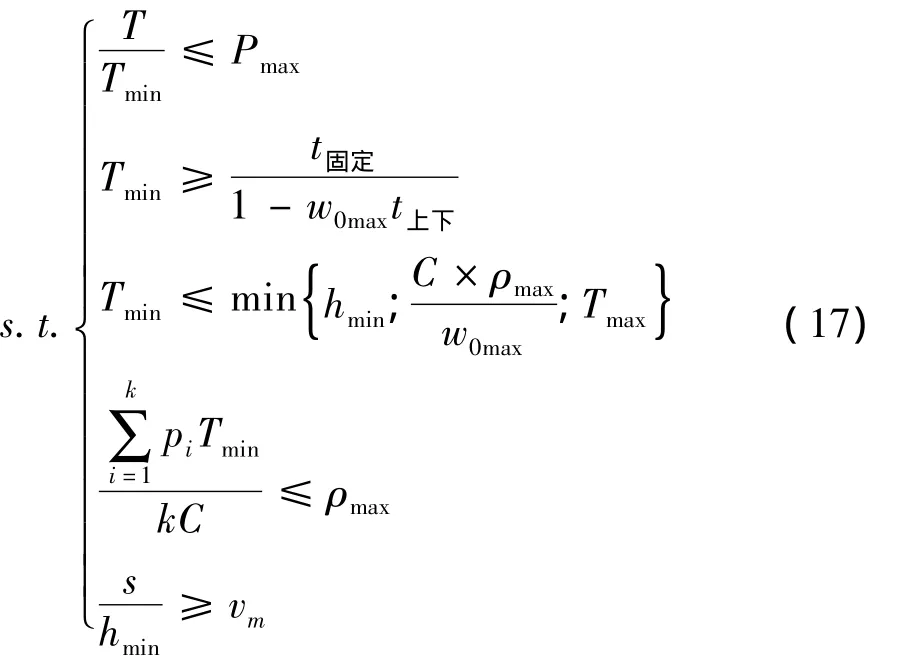
第1个约束条件表示线路配车数不能大于该线路最大配车数;第2、3个约束条件为不出现列车化现象条件下的最小发车间隔的取值范围,在原有的基础上加入了公交公司所允许的最大发车间隔;第4个约束条件表示车辆在所有公交车站处的平均满载率不能大于按乘客舒适程度确定的最大值;第5个约束条件表示车辆在路段上运行存在最小车头时距时车辆的运行速度应不小于临界速度。
3.5 模型求解
1)化简约束条件,得到最终约束条件为:

令:
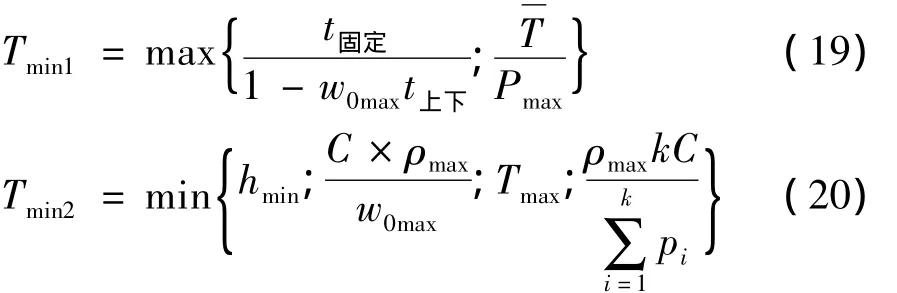
2)对目标函数化简,令:
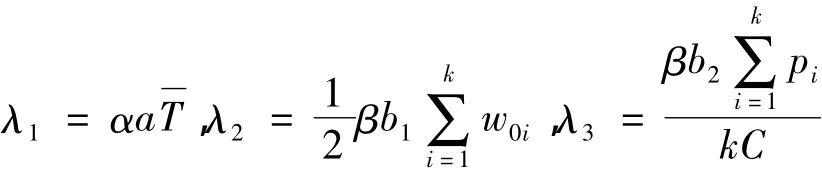
化简后的模型为:

3)对目标函数求导,令导函数等于0,解得该方程必然存在的一个实根,得到最小发车间隔的值。同时根据现有条件计算式(21)约束条件的值,来判断结果是否合理。
3.6 模型评价
从定性的角度来看,本模型的优越性在于:①为缓解公交列车化现象,设置了最小发车间隔变量,并将不发生列车化现象作为一个约束条件来确定最小发车间隔的取值范围;②在考虑到增加不发生列车化现象作为约束条件的同时,还考虑到了运营成本和乘客服务水平的因素,尽量做到运营成本最小、乘客利益最大,顾及到了双方的利益。
本模型的的不足之处有:①模型部分假设条件较理想化。如本模型假设所有在车站候车的乘客在车辆到达时均上车,假设某特定运行区间内在特定时间段内平均运行速度为恒定值等。②经验折算系数和权重系数的取值上带有主观因素,影响计算结果。
从定量的角度看,可以用以下两个指标来对模型进行评价:
1)公交列车化现象出现概率
根据式(1),令其中变量:

式中:λ为车辆到达率,辆/min。
将该模型求得的最小发车间隔、原有的最小发车间隔代入式(22)和式(1)中,计算P(h≤t),比较其结果可得该模型效果优劣。
2)总成本
总成本即该模型的目标函数最优解。将求得的最小发车间隔和原有的最小发车间隔代入式(16)进行计算,比较其结果可得该模型效果优劣。
4 实例分析
4.1 线路基本情况
选取成都市81路公交车作为分析对象。该线路公交车由金沙公交站开往五桂桥站,全长14.2 km,共设18个车站。该线路车辆主要在公交专用道上行驶。乘客候车规模较大的车站为金河路至水碾河之间的车站,对应的运行区间占线路全长31%,公交列车化现象明显,同时其客流变化规律也有典型代表性。
4.2 参数取值
根据实地调查,81路公交车由金沙公交站至五桂桥站运行时全线车站单位时间内乘客候车规模w0i的值和单向断面流量pi的值如表1。
4.3 计算结果及评价
根据该模型计算结果,81路公交车在平峰时期的最小发车间隔应设置为4 min。根据约束条件得出,当最小发车间隔取值在3.44~6 min间隔内,车辆全线运行时不会发生列车化现象。若按原有的调度计划,平峰时期的发车间隔为3 min,不能满足这一条件。
4.3.1 公交列车化现象出现概率P(h≤t)
1)按原有发车间隔计算。车辆到达率λ=0.33辆/min。将该值代入式(1),取参数τ=0.018 min,t=1 min,P(h≤t)=0.275。
2)按本文模型计算。车辆到达率λ=0.25辆/min。将该值代入式(1),取参数 τ=0.018 min,t=1 min,得到 P(h≥t)=0.855,P(h≤t)=0.145。按本文模型计算出的最小发车间隔进行发车时,公交列车化现象出现概率比按原有发车间隔进行发车时小,证明本文模型有一定优化作用。
4.3.2 总成本 C(Tmin)
1)按原有发车间隔计算。最小发车间隔Tmin=T=3 min,其它参数按照4.2节进行取值,并代入式(16),得到结果C(Tmin)=2 026(货币单位)。
2)按文中模型计算。最小发车间隔 Tmin=4 min,其它参数按照4.2节中进行取值,并代入式(16),得到结果C(Tmin)=1 900(货币单位)。按文中模型计算出的最小发车间隔进行发车时,总成本比按原有发车间隔进行发车时小,证明本文模型具有一定优化作用。
5 结语
将确定公交车最小发车间隔的方法同缓解公交列车化问题进行交叉研究,得出以下结论:
1)对于特定公交线路全线运行过程中发生的串行现象,可以采用移位负指数分布的分布函数进行定量描述。
2)在特定的公交线路上产生串行现象的因素主要有乘客候车规模、区间平均运行速度、发车间隔、车站泊位数和平均站距。
3)最小发车间隔应至少确保两个条件:①满足公交公司效益,即全线不出现串行运行;②满足乘客利益,即至少确保乘客服务水平在原有基础上不变。
4)以缓解列车化现象为约束条件,最小发车间隔为决策变量,公交公司运营成本和乘客出行成本之和最小为目标函数的计算模型是一种在缓解公交列车化现象条件下的新型最小发车间隔求解方法,并具有可行性和有效性。
[1]刘咏梅.深圳市公交列车化引发的思考[J].公路与汽运,2011(1):40-42.Liu Yongmei.Thoughts for high-frequency of bus operation in Shenzhen[J].Highways & Automotive Applications,2011(1):40-42.
[2]Ceder A.Bus frequency determination using passenger count data[J].Transportation Research(Part A):General,1984,18(5/6):439-543.
[3]Ceder A.Methods for creating bus timetables[J].Transportation Research:Part A General,1987,21A(1):59-83.
[4]孙芙灵.公交调度中发车间隔的确定方法的探讨[J].西安公路交通大学学报,1997,17(2):44-48.Sun Fuling.The research of methods for determining bus headway[J].Journal of Xi’an Highway University,1997,17(2):44-48.
[5]程杰,邓卫,蒯婷婷.基于期望满足概率的公交车发车间隔计算模型[J].现代交通技术,2006(4):47-49.Cheng Jie,Deng Wei,Kuai Tingting.The calculation model of bus frequency based on expected probability[J].Modern Traffic Technology,2006(4):47-49.
[6]覃运梅,王玲玲.基于遗传算法的公交发车间隔模型[J].交通标准化,2009(2/3):110-113.Qin Yunmei,Wang Lingling.Bus departure interval model based on genetic algorithm[J].Communications Standardization,2009(2/3):110-113.
[7]张晓培,李茂军.遗传-牛顿算法在公交智能调度中的应用[J].计算机测量与控制,2010,18(12):2830-2832.Zhang Xiaopei,Li Maojun.Application of Genetic-Newton algorithm in public transport dispatching[J].Computer Measurement& Control,2010,18(12):2830-2832.
[8]李江.交通工程学[M].北京:人民交通出版社,2002:97-99.
[9]帅斌,霍娅敏.交通运输经济[M].成都:西南交通大学出版社,2007:98-100.

