地下结构波动法与振动法的对比

高 峰，孙常新，2，赵冯兵

(1.重庆交通大学山区桥梁与隧道国家重点实验室培育基地，重庆 400074;

2.华北水利水电学院，河南郑州 450011;3.重庆能源职业学院，重庆 400041)

地下结构波动法与振动法的对比

高 峰1，孙常新1，2，赵冯兵3

(1.重庆交通大学山区桥梁与隧道国家重点实验室培育基地，重庆 400074;

2.华北水利水电学院，河南郑州 450011;3.重庆能源职业学院，重庆 400041)

介绍了波动法和振动法的计算原理和使用方法，用这两种方法计算人工地震波，分析两种方法的区别。结果表明:波动法和振动法的计算数值和变化规律基本一致;波动法可以反映波动传播的时间效应，振动法不能反映波动传播的时间效应，但振动法计算步骤简便，精度可以满足要求;建议在地下结构动力分析中使用振动法。

波动法;振动法;计算原理;地震波;人工边界条件

0 引言

近年来，随着在地震中地下结构的大量损坏和计算手段的快速发展，地下结构的地震计算方法引起了人们的重视并获得快速发展。地下结构地震时程分析的常用方法主要有两种:一种是以求解波动方程为基础的波动法，另一种是以求解结构运动方程为基础的振动法。波动法将地下结构与其周围地层介质作为一个整体来进行分析，假定地下结构的存在对波动场的影响可以忽略不计，按波动方程求解地下结构与其周围介质中的波动场和应力场;振动法以结构为主体求解其地震运动，将地震作用以地震加速度形成的惯性力形式施加到结构上，建立地下结构的地震运动方程，按运动方程求解地下结构的地震响应［1］。

当前，使用波动法进行地下结构计算分析主要研究成果有:Pao和Mow［2］采用波函数展开法开创性地研究了无限空间中单个洞室在弹性波入射下的动应力集中问题;20世纪90年代，Lee和Karl［3］采用大圆弧假定法给出了半空间中单个洞室对P波和SV波的散射解析;梁建文，等［4］用大圆弧假定法分析研究了半空间中双洞室对P波和SV波的散射并得出解析解;黄艳，等［5］基于波动控制方程研究了以任意方向入射的平面SH波在浅埋多个圆孔处的散射与地震动问题;刘晶波，等［6］应用弹性波动理论，发展了实现波动直接模拟的三维时域黏弹性人工边界，可以方便地应用于三维波动问题的模拟分析;潘旦光，等［7］将波动理论和随机振动理论结合起来，提出了P波和SV波作用下层状土层地震反应分析的随机波动分析方法;黄胜，等［8］基于无限元人工边界的合理地震动输入方法，考虑到地层的辐射阻尼和地震波在地层中的反射和散射，采用波场分解的方法给出地震波从底面垂直入射时不同边界面上的等效地震荷载的计算公式。振动法是动力计算较常用的方法，近年来的主要研究成果有:李辉，等［9］基于振动法推证出以地表地震动作为输入的自由地基地震反应分析模型;刘如山，等［10］基于振动法从地震时一维土层反应应力入手，对有限元反应加速度法的地震荷载加载方法进行改进，提出了有限元反应应力法;胡世丽，等［11］从概念、建立方程、求解方程和适用范围多个方面阐述了波动和振动的区别和联系。

当前，波动法和振动法应用于地下结构地震分析已比较成熟，并取得了不少成果。但是两种方法有何区别，至今未见到相关文献。笔者将两种方法进行了对比研究，得出了具有一定应用价值的结论。

1 计算原理与方法

波动法和振动法用于地下结构地震时程分析时的出发点不同，两者的计算原理和使用方法有所不同，各具特点。

1.1 波动法计算原理

20世纪70年代，前苏联的乌兹别克、格鲁吉亚等对深埋隧道采用了弹性波动理论拟静力法进行计算，出现了连续介质弹性力学法［12］，现行的波动法正是在此基础上发展而来的。

波动法中波动输入方式主要有两种:①直接在人工边界上实现波动输入，通过对人工边界和内结点波动的反复叠加或减去已知的自由波场的方法完成波动输入［13］，主要在解析计算中使用，称之为波动(解析)法;②将人工边界上的自由场位移作为时变外荷载输入，主要在数值计算中使用，称之为波动(数值)法。自由场位移可以由初始数据得到，相当于将波动输入问题转化为点源问题进行求解分析。

1.1.1 波动(解析)法

波动(解析)法是对波动物理过程的模拟［14］。为说明问题，针对图1的简单人工地震波动(波速为c)进行计算分析。

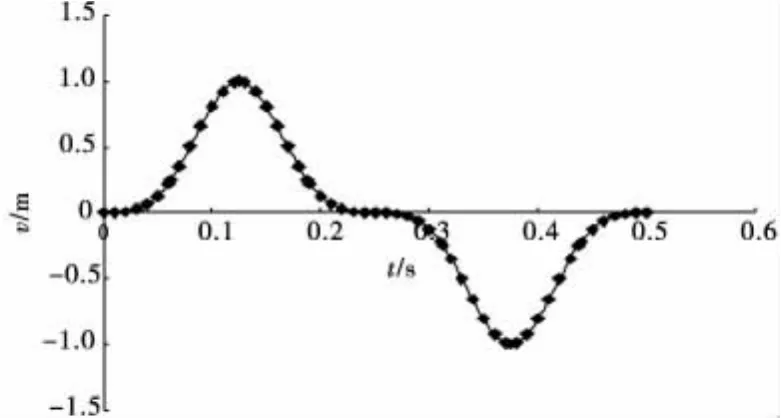
图1 人工地震波v(t)时程Fig.1 Artificial seismic wave schedule of v(t)

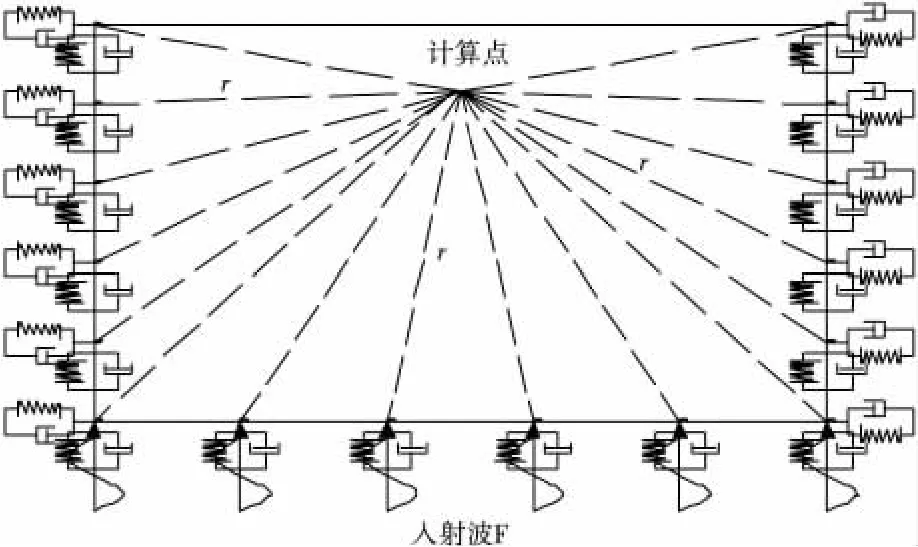
图2 波动法计算示意(P波)Fig.2 Calculation of wave method(P wave)

对图2中的矩形计算区域(高H)，设v(t)于t=0时刻由底部输入向上传播，在时刻t=H/c时上行波到达自由顶面，由此产生一个反射波，此下行波为上行入射波的镜面映像。当下行波在t=2H/c时刻到达基底时，完成了波动过程的第一个循环。然后，由于基底采用的是黏弹性边界，到达基底的下行波将被完全吸收，波动循环完成。设波动在传播过程中没有能量损失，则在波动循环中陆续增加的反射波动如式(1):

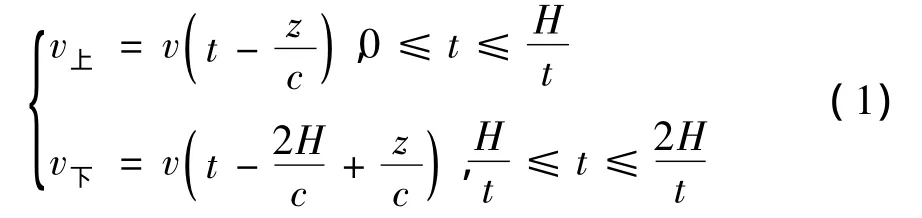
式中:z为计算点到基底的竖直距离，m。

由式(1)即可求得计算区域内任一点的波动位移，从而可以得到计算区域内的波动场。由位移公式求导可得到速度场，由速度公式求导可得到加速度场，即可对波动场中的地下结构进行波动求解。

图3为由波动法计算得到的计算区域内的波动场。

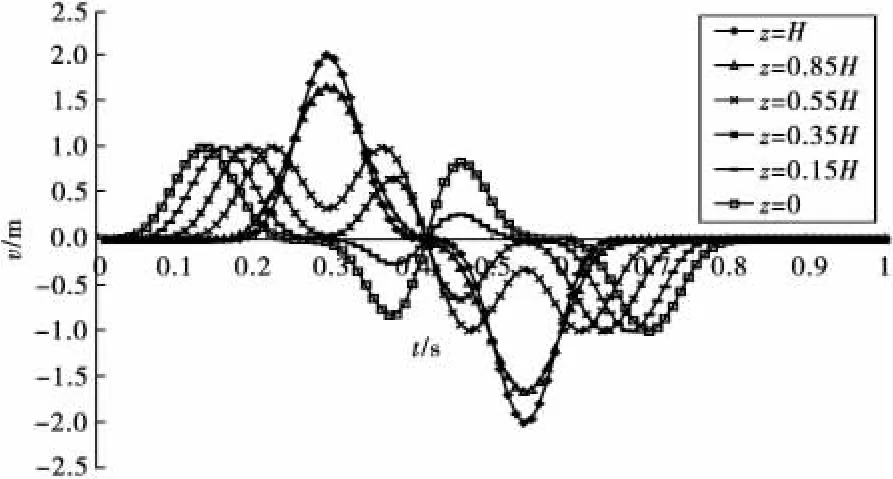
图3 不同深度处v(t)时程曲线Fig.3 Different depths schedule curve of v(t)

由图3可知:上行波传到顶面时v(t)变为原先的两倍;不同深度处的v(t)不仅振幅不同，在相位上也有所区别。这些情况与波动理论相符。波动(解析)法是基于波动基本理论的通用方法，计算结果精确可信，但在有限元计算分析中使用不方便，具体有限元计算中常采用波动(数值)法。

1.1.2 波动(数值)法

波动(数值)法是依据波动场，将输入波动转化为直接作用在人工边界上的等效荷载来实现波动输入，即把波动作用转换成人工边界节点作用力来实现波动的模拟。波动(数值)法方便地运用于有限元数值计算分析中。有限元分析必定是针对有限范围计算区域的计算，这就需要在半无限地下空间中截取有限的计算区域出来，截取的边界上要采用人工边界以模拟无限边界条件，目前常用的是黏弹性人工边界。

对于平面内的柱面波(以P波为例)，其波动方程可以表示为:

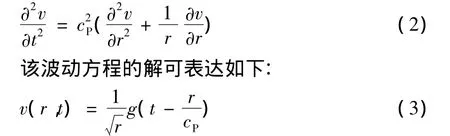
式中:g为任意函数。

经推导，可得任一半径rb处的应力，可用该处的速度和位移表示:

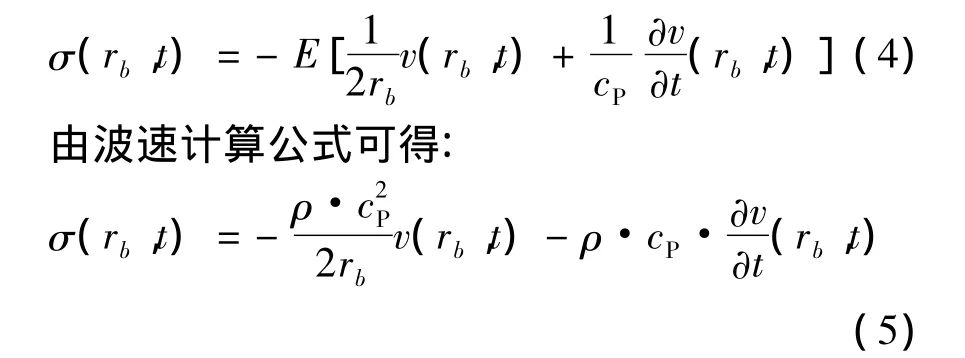
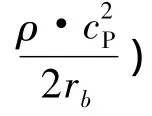
为实现波动输入，在人工边界上施加总应力σZ，采用力学中分离隔离体概念［15］，将人工边界与附加其上的物理元件脱离，则总应力σZ包括对边界施加的应力σ0，使人工边界上的节点产生位移为v0的运动，和对物理元件上施加应力σ1(σ1=-σ)，使物理元件上的节点产生位移为v0的运动，即:

由式(8)可推导出需要在人工边界节点处施加的等效节点荷载的计算公式，进而可以在地下结构上施加等效节点荷载进行有限元计算，完成地下结构在地震荷载作用下的动力时程分析。

1.2 振动法计算原理

振动法是当前地下结构动力时程分析的通用方法，1900年日本大森房吉教授提出了计算地震荷载的静力理论［16］，假定地震时结构各部分都有一个与地震加速度大小相同的加速度，作用于结构上的水平地震力等于结构自重乘以某一地震系数来计算结构的变形与内力(地震系数法)。该方法简单方便，且经受过一般地震的考验，许多国家的抗震设计规范都采用过。我国地下结构的抗震设计20世纪60年代以来沿用地震系数法，至今仍为隧道设计规程所采用。现行的振动法正是在此基础上发展而来的。

结构体系承受相同的平动运动的地震反应体系的运动方程为［17］:

式中:上标t表示总位移。

式(9)表示，引起体系动力反应的有效地震力依赖于总运动惯性力，而阻尼力和弹性力只依赖于相对运动。

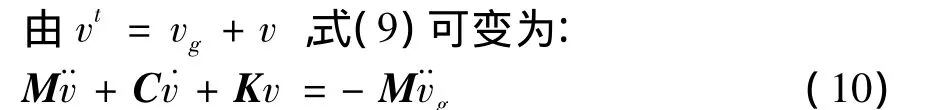
若阻尼力和弹性力用总运动与地面运动的差来表示，则式(9)可写成:

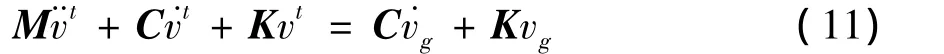
式(10)、式(11)即振动法的基本原理公式。原则上，地震反应问题可用式(10)和式(11)来求解，实际上，因为式(11)的地震应力的表达式较复杂，同时由于地震运动通常以地面加速度来表示，故式(10)较常用。

常用振动法的基本原理，即式(10)可用矩阵的形式表示如下:

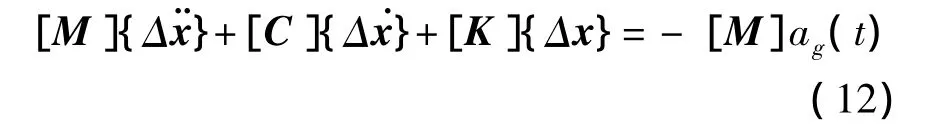
式中:［M］为计算结构质量矩阵;［C］和［K］分别为ti时刻计算结构阻尼矩阵和刚度矩阵;ag(t)为第i+1时段内(ti到ti+1)输入的波动加速度增量，{Δ¨x}、{Δ˙x}和{Δx}为第i+1时段内各质点相对加速度、相对速度和相对位移的增量所组成的列向量。

式(12)常采用数值解法，主要有线性加速度法、威尔逊θ法、中点加速度法、纽马克β法和龙格-库塔法等，其通用计算步骤如下［18］:

1)将整个波动时段划分为一系列的微小时段Δt，通常取(0.01 ～0.02)s;

2)对实际波动加速度记录，经过零线调整等一些必要的处理后，按时段Δt进行数值化;

3)在每一个微小时段 Δt内，把 M、C、K及ag(t)均视为常数;

4)利用第i+1时段(ti到ti+1)的前端值{xi}、{˙xi}、{¨xi}来求该时段的末端值{xi+1}、{˙xi+1}、{¨xi+1}。循序渐进地对每一时段重复上述步骤，即得整个时程的结构波动反应。

式(12)中方程左端的加速度、速度、位移为相对数值，使用式(12)算出来的结果也应该是相对值。这种方法存在的缺陷是，采用统一的加速度输入不能考虑波动传播的时间效应;计算出的结果是相对值，还需要和输入值进行叠加换算后得到绝对值。但该方法计算简便，在当前的地下结构地震分析中被大量地采用。

图4为振动法计算示意，其中计算模型底部设置成固定约束以反映底层基岩较坚硬的性质(具体对比中发现此种边界条件较合理，此处不再详述)，这是对通常振动法中采用3侧黏弹性边界条件的一种修正。加速度场可由现场实测或人工合成得到。

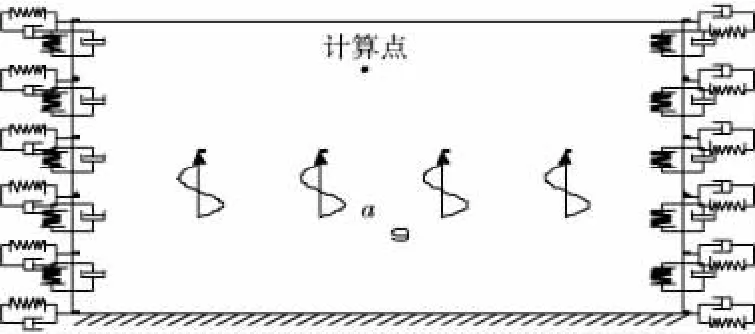
图4 振动法计算示意Fig.4 Calculation of vibration method

2 计算结果对比

波动法和振动法的计算原理和使用方法有所区别，笔者采用这两种方法针对人工地震波(图1)进行了计算，并对两者的位移和应力计算结果进行了对比分析。

具体的计算参数为［15］:地层的剪切模量 G=5.292 MPa，弹性模量 E=13.23 MPa，泊松比 ν=0.25，密度为 ρ=2.7 kg/m3，计算模型 381 m ×762 m的长方形，采用有限元软件ANSYS进行计算，计算模型如图5。

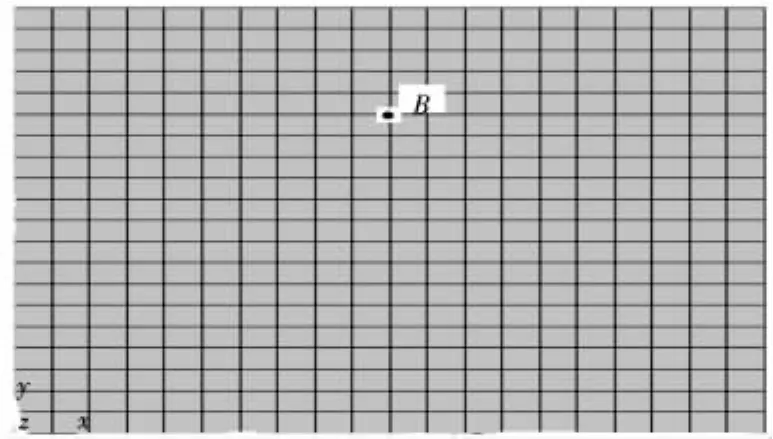
图5 有限元计算模型Fig.5 The finite element calculation model

计算中输入波动采用周期性的人工地震波，其振幅为1 m，周期为0.5 s(图1)。

对计算模型中计算点B(顶面以下57.15 m)处的计算结果对比分析如图6。

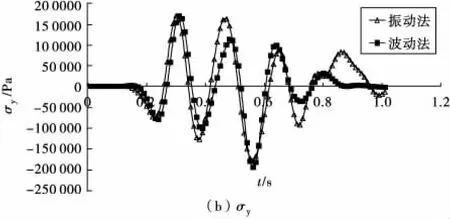
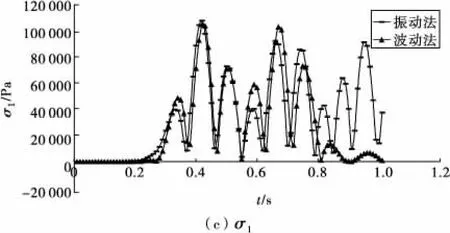
图6 波动法与振动法计算结果对比Fig.6 Contrast of calculation results of wave and vibration method

2.1 竖向位移对比

由图6(a)可以看出:①波动(数值)法的计算结果和波动(解析)法基本一致，鉴于波动(数值)法便于实现，可直接运用波动(数值)法来代表波动法;②波动法所得的y方向位移值和振动法相比相差不大，变化规律基本相同;③波动法所得的y方向位移值和振动法相比在时间上有所滞后，说明两种方法所反映的时间效应不同;④当时间t较大时(波动从底面两次向上反射传播到计算点以后)，振动法的计算结果明显增大，这是因为振动法采用的是固定底边界而不是采用具有吸波功能的黏弹性边界。

2.2 竖向应力对比

由图6(b)可以看出:①由波动法和振动法计算所得的竖向应力的数值和变化规律基本相同;②两者的计算结果在时间上稍有差别，当t较大时两者出现较大差异，这是由于两者的底部边界条件有所不同造成的;③波动法的计算结果随时间衰减稍快，这主要是因为波动法中设置的底部黏弹性边界具有吸波效应。

2.3 最大主应力对比

由图6(c)可以看出:①由波动法和振动法计算所得的最大主应力的数值和变化规律基本相同;②波动法和振动法计算所得的最大主应力的极值时刻基本相同;③波动法的计算结果随时间衰减稍快。

3 结论

将振动法和波动法这两种常用的动力分析方法分别针人工地震波进行了对比计算分析，得到如下结论:

1)采用波动法和振动法进行动力分析所得的计算结果基本一致，振动法可以满足精度要求。

2)波动法采用3侧黏弹性边界，而使用振动法时一般要在计算模型底部采用固定边界，两者一般取不同的边界条件。

3)振动法和波动法所得的位移和应力计算结果数值和变化规律基本一致。

4)波动法反映了动力计算的实质，可以体现出波的传播时间效应，但是计算较为繁琐，振动法不能反映波动的时间效应，但是计算简便，计算结果与波动法基本一致，实用性较强。建议在地下结构动力分析中使用振动法。

［1］严松宏.地下结构随机地震响应分析及其动力可靠度研究［D］.成都:西南交通大学，2003.

［2］ ［美］Pao Y H，Mow C C.弹性波的衍射与动应力集中［M］.刘殿魁，苏先樾，译.北京:科学出版社，1993:39-78.

［3］Lee V W，Karl J.On deformations near a circular underground cavity subjected to incident plane P waves［J］.European Earthquake Engineering，1993，7(1):29-36.

［4］梁建文，张郁山，顾晓鲁.圆弧形层状沉积河谷场地在平面SH波入射下动力响应分析［J］.岩土工程学报，2000，22(4):396-401.

Liang Jianwen，Zhang Yushan，Gu Xiaolu.Surface motion of circular-arc layered alluvial valleys for incident plane SH waves［J］.Chinese Journal of Geotechnical Engineering，2000，22(4):396-401.

［5］姜艳，黄荣富，刘殿魁，等.SH波在浅埋多个圆孔处的散射与地震动［J］.地震工程与工程振动，2004，24(1):7-14.

Jiang Yan，Huang Rongfu，Liu Diankui，et al.Scattering of SH-wave by shallow fill multiple circular cavities and the ground motion［J］.Earthquake Engineering and Engineering Vibration，2004，24(1):7-14.

［6］刘晶波，王振宇，杜修力，等.波动问题中的三维时域黏弹性人工边界［J］.工程力学，2005，22(6):46-51.

Liu Jingbo，Wang Zhenyu，Du Xiuli，et al.There-dimensional viscoelastic artifical boundaries in time domain for wave motion problems［J］.Engineering Mechanics，2005，22(6):46-51.

［7］潘旦光，楼梦麟，董聪.P、SV波作用下层状土层随机波动分析［J］.工程力学，2006，23(2):66-71.

Pan Danguang，Lou Menglin，Dong Cong.Random Wave-theory analysis of layered soil sites under P-and SV-wave excitations［J］.Engineering Mechanics，2006，23(2):66-71.

［8］黄胜，陈卫忠，伍国军，等.地下工程抗震分析中地震动输入方法研究［J］.岩石力学与工程学报，2010，29(6):1254-1262.

Huang Sheng，Chen Weizhong，Wu Guojun，et al.Research on seismic wave input with three-dimensional viscoelastic artificial boundary［J］.Chinese Journal of Rock Mechanics and Engineering，2010，29(6):1254-1262.

［9］李辉，刘立平，赖明.基于地面地震反应输入的自由场地震反应分析［J］.四川建筑科学研究，2004，30(3):94-97.

Li Hui，Hiu Liping，Lai Ming.The analytical model of free field ground action as the inputing strong motion record getting from the surface［J］.Sichuan Building Science，2004，30(3):94-97.

［10］刘如山，胡少卿，石宏彬.地下结构抗震计算中拟静力法的地震荷载施加方法研究［J］.岩土工程学报，2007，29(2):237-242.

Liu Rushan，Hu Shaoqing，Shi Hongbin.Study on seismic loading of pseudo-static approach used in the seismicdesign of underground structure［J］.Chinese Journal of Geotechnical Engineering，2007，29(2):237-242.

［11］胡世丽，李贵荣.振动力学和波动力学的讨论［J］.采矿技术，2010(7):115-116.

Hu Shili，Li Guirong.Discussion of vibration mechanics and wave mechanics［J］.Mining Technology，2010(7):115-116.

［12］ St john C M，Zahrah T F.Aseismic design of underground structures［J］.Tunnelling and Underground Space Technology，1987，2(2):165-197.

［13］吕斌，李杰.确定性波动输入条件下的地震动场数值模拟［J］.工程力学，2002，19(增刊 1):74-79.

Lv Bing，Li Jie.Numerical simulation for seismic field at the condition of inputting earthquake ensurely［J］.Engineering Mechanics，2002，19(supp1):74-79.

［14］ 廖振鹏.工程波动理论导论［M］.北京:科学出版社，2004:5-10.

［15］吕彦东.结构-地基动力相互作用分析方法的研究［D］.北京:清华大学，1997.

［16］胡聿贤.地震工程学［M］.北京:地震出版社，1988:129-160.

［17］克拉夫.结构动力学［M］.王光远，译.北京:科学出版社，1981:362-363.

［18］陈伯望，孟茁超.结构地震反应分析方法的对比研究［J］.湖南城市学院学报，2003，24(6):6-9.

Chen Bowang，Meng Zhuochao.Comparative study of analytical methods of seismic reaction of structure［J］.Journal of Hunan City University，2003，24(6):6-9 .

Contrast of Wave and Vibration Methods for Underground Structure

Gao Feng1，Sun Changxin1，2，Zhao Fengbing3
(1.State Key Laboratory Cultivation Base for Bridge and Tunnel Engineering，Chongqing Jiaotong University，Chongqing 400074，China;2.North China University of Water Resources and Electric Power，Zhengzhou 450011，Henan，China;3.Chongqing Energy College，Chongqing 400041，China)

Calculation theories and methods are introduced respectively in this paper;artificial seismic wave was calculated by wave method and vibration method respectively and the difference of these two methods has been analyzed.The analytical results indicate that:the calculating values and changing rules of wave method and vibration method are almost accordant;the wave method can reflect the time effects for the transition of wave while the vibration method cannot;the vibration method has the following advantages:its calculating steps are simple;its calculating precision can meet the needs.Therefore，vibration method is suggested to be used for the dynamical analysis of underground structure.

wave method;vibration method;calculation theories;seismic wave;artificial boundary condition

U451

A

1674-0696(2012)04-0764-05

10.3969/j.issn.1674-0696.2012.04.07

2011-11-16;

2012-01-15

国家自然科学基金项目(51178490);中铁二院工程集团有限责任公司科研项目(科2009-31);重庆市教委科学技术研究项目(KJ090403);华北水利水电学院2009年度青年科研基金项目(HSQJ2009013);山区桥梁与隧道工程国家重点实验室开放基金项目(CQSLBFY12-2);重庆交通大学(桥梁)结构工程重点实验室开放基金项目(CQSLBF-Y10-8)

高 峰(1964—)，男，浙江云和人，教授，博士生导师，博士，主要从事地下结构设计与施工方面的教学研究工作。E-mail:gaofeng1964@163.com。