Frost Resistance and Damage Velocity of Compressively Preloaded Concrete

CHEN Si-jia(陈思佳)，SONG Xiao-bing(宋晓冰)，LIU Xi-la(刘西拉)

School of Naval Architecture，Ocean＆Civil Engineering，Shanghai Jiaotong University，Shanghai 200240，China

Introduction

In cold regions，freeze-thaw attack is one of the main factors which influence durability ofconcrete［1-4］. Many researches have been conducted on frost resistance of concrete in recent years，which mainly focus on the following aspects:the effect of mix proportion of concrete on the frost resistance［5-8］，prediction method of concrete freeze-thaw durability［9-11］，frost resistance of special concrete［12-14］，behavior of concrete after freeze-thaw cycles［15］，frost resistance of concrete subjected to multi-damaging processes［16-18］，and so on.However，there are still some limitations of most existing researches.

Firstly，most previous researchers focused on the freezethaw durability of concrete without external loads.Almost all related standards and codes used for testing frost resistance of concrete did not take into account the effect ofexternal loads［19-21］.However，most concrete structures in cold regions，such as bridges and pavements，are subjected to both external loads and freezing-thaw cycle.The mechanical properties of concrete in these regionsare determined by freeze-thaw damage，load damage，and their coupling effect.Usually，the combined effect of resulting stresses and freeze-thaw cycles causes deterioration of concrete properties.It is necessary to know how the loads influence the concrete resistance to freezing and thawing.

Secondly，with regard to the influence of the external loads［16-18］，only the frost resistance of mortar or plain concrete was discussed in the past.It is well known that the control stress for flexural loaded mortar or plain concrete is tensile stress，which means that the flexural loaded specimen will fracture if the tensile stress caused by both flexural load and frost action reaches the specimen's residual tensile strength.However，for most flexural loaded reinforced concrete(RC)members，concrete resists compressive stresses whilst reinforcement resists the tensile stresses，which is attributed to the fact that concrete is strong in compression but weak in tension.Comparing with flexural load，it seems that the research on frost resistance of concrete under compression is more attractive in engineering community.

Thirdly，the dynamic modulus of elasticity and weight loss were the main focuses for almost all previous researches.However，engineers are mainly concerned with the residual strength of concrete after freeze-thaw cycles，because it can directly affect the serviceability and safety of RC structures.The investigation of residual compressive strength of concrete after freeze-thaw cycles is more significant in practice.

In the present work，specimens were compressed by specially designed apparatus while suffering freeze-thaw cycles，and their residual strength after each freeze-thaw cycle was obtained by nondestructive tests.The frost resistance and compressive strength degradation of concrete were investigated comprehensively.

1 Experimental

1.1 Sample preparation

A Chinese standard(GB175—2007)325#portland cement(which has standard compressive strength of 32.5 MPa at the age of 28 d)was used in the experiment.River sand with fineness modulus of 2.3 was used.Coarse aggregate was crushed stones with diameters from 5-10 mm.The proportions of the various concrete mixes and the major parameters are listed in Table 1.

Table 1 Mix proportions and major parameters of concrete

More than 130 concrete prisms with 40 mm×40 mm×160 mm were made.Four types of concrete were studied:three types of non-air-entrained concrete with water/cement(w/c)ratio of 0.47，0.59，and 0.67(designated as E-0.47，E-0.59，and E-0.67 respectively);one type of air-entrained concrete with 1.01 kg · m-3air-entraining agent and w/c=0.47(designated E-0.47A).All specimens were demolded after 24 h of casting and cured in a condition of(20±3)℃ and 95%RH for 23 d.Thereafter，the specimens were immersed in water for 4 d prior to the freezing and thawing cycles.

1.2 Preloading details

The specimens were subjected to uniaxial compression.For each type of concrete，the averaged compressive strength was obtained by three testing samples before freezing and thawing，and the result was used as the basis for determining the preloading strength level.The uniaxial compressive strength values are given in Table 1.Before freeze-thaw testing，the concrete prisms were compressively preloaded，and the maximum load applied to each prism was adjusted to generate a maximum compressive stress of 0，30%，50%，and 80%(i.e.，the stress ratios are 0，0.3，0.5，and 0.8)of the compressive strength of the same prism.According to each concrete mix proportion，three specimens were measured.Preloading was generated through a specially designed apparatus，as shown in Fig.1.The applied force was controlled and checked by the protected sensors［22］to prevent the stress relaxation under freeze-thaw cycles.

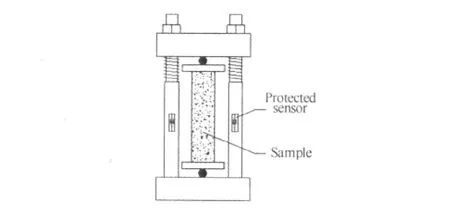
Fig.1 Schematic description of the loading device

1.3 Freeze-thaw test

At the age of 28 d，tests of the concrete were carried out for suffering of the freeze-thaw cycles and external loads according to ASTM C666［19］.

1.4 Ultrasonic method and preliminary test

The residual compressive strength of each specimen after every freeze-thaw cycle was obtained by ultrasonic method［23-25］with the concrete strength versus ultrasonic pulse velocity relationship.It is known that many factors(age，porosity，composition，curing and so forth)which influence concrete strength and also interfere with the determination of concrete strength by ultrasonic means［25］.It is noted that in order to accurately evaluate the concrete compressive strength with this method，individual relationship between concrete strength and ultrasonic velocity for each type of concrete is obtained by preliminary tests.

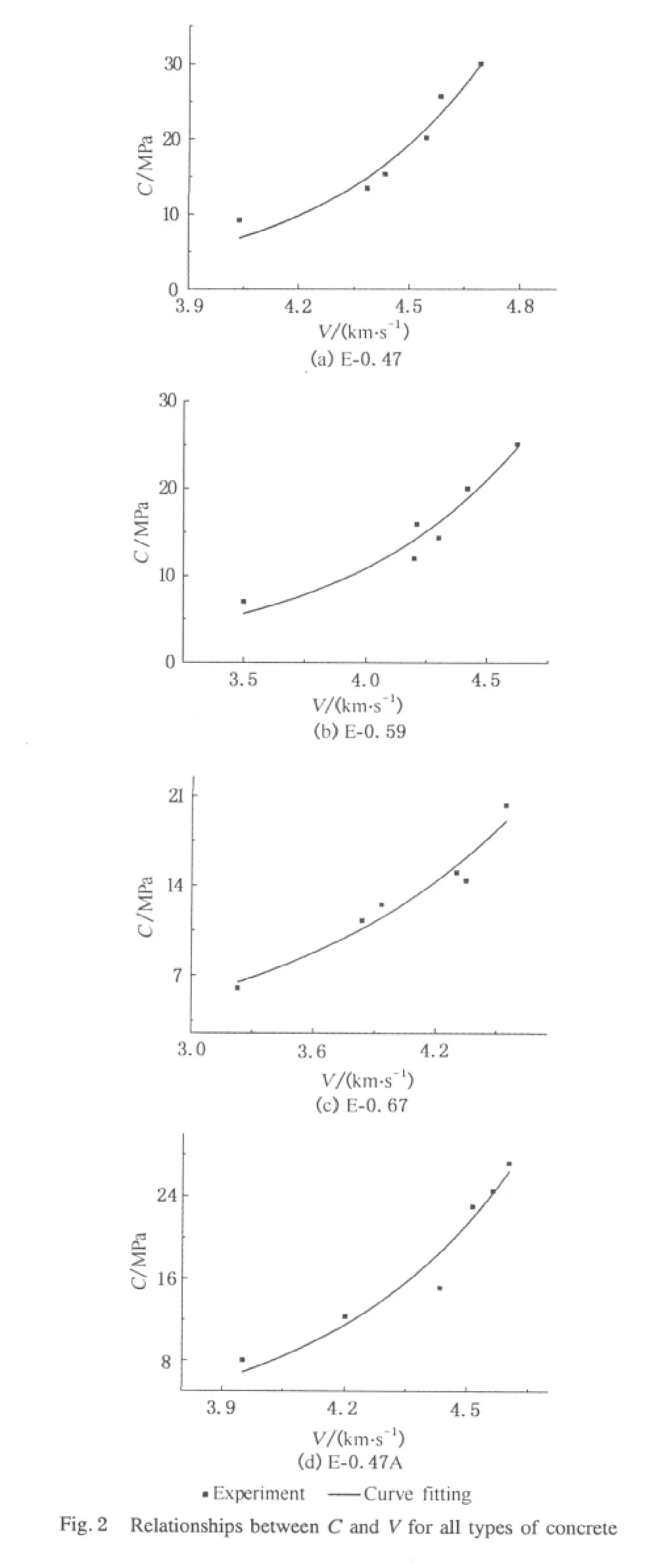
Firstly，six preloaded specimens of each mixture after suffering different freeze-thaw cycles were chosen to measure the transit time of ultrasonic pulse through the specimens，from which the ultrasonic pulse velocity for each specimen then could be obtained.Secondly，the uniaxial compression tests were performed on the same specimens to obtain the residual compressive strength.Consequently，the empirical formula for each concrete mix was derived by regression analysis between compressive strength and ultrasonic pulse velocity.Table 2 and Fig.2 present the relationships between concrete compressive strength C and the ultrasonic pulse velocity V，along with the coefficients of determination R2.With the empirical formulas，the residual compressive strength of each preloaded specimen after every freeze-thaw cycle could be obtained by measuring the transit time of ultrasonic pulse passing through the specimen.

The ultimate number of freeze-thaw cycles up to failure was also monitored.The number of cycles to failure for unpreloaded specimens was recorded when the ratio of residual strength to initial strength reached 0.3.For preloaded specimens，the number of cycles to failure was recorded at the time the sample fractured.

Table 2 Relationships between concrete compressive strength(C)in MPa and ultrasonic pulse velocity(V)in km/s

2 Results and Discussion

2.1 Resistance to freezing-thawing of preloaded specimens

2.1.1 Influence of preloading level

Thenumbersoffreeze-thaw cyclesto failureunder different preloading levels for four types of concrete are shown in Fig.3.It is found that preloading level influences the frost resistance ofconcrete.Comparing each typeofconcrete subjected to pre-stress ratio 0 to 0.8，the number of cycles to failure becomessignificantly smallerwith pre-stressratio increasing.For example，the number of cycles to failure for E-0.47 is more than 140 without external loading，while the number is less than 20 with the pre-stress ratio of 0.3.And at the stress ratio of 0.8，all the types of concrete can suffer only a few freeze-thaw cycles，with strength dropping to almost zero.As the preloading level increases，the number of cycles to failure for each concrete decreases，which means that external loading makes the failure of concrete exposed to freeze-thaw cycles earlier.

Fig.3 Number of freeze-thaw cycles to failure for all types of concrete

Generally，this is because the samples preloaded at higher level need less strength loss to fail.Furthermore，preloading affects the mechanism of failure.In the experiments reported here，specimens were under simultaneous action from both freeze-thaw cycles and compression.In this case，the internal hydraulic pressure caused by freeze-thaw cycles was equally distributed tension in all directions while the compression from external load was in one direction.Since the compressive stress was higher than the tensile stresses，the preloaded specimens were actually under triaxial loading，which contained one directionalcompression and two directional homogenous tensions perpendicular to the compressive direction.

It is known that，in the three dimensional principal stress space，the compressive meridians of the failure surface of concrete are the intersection curves between the failure surface and the meridian plan containing the hydrostatic axis with θ=60°［26］，as shown in Fig.4.For a point in the meridian，in the first quadrant of the coordinate system shown in Fig.4，the coordinates of the point represent two equal principal tensile stresses and one principal compressive stress which can cause concrete failure.As previously discussed，for concrete，the compressively preloading produces one principal compressive stress，and hydraulic pressure produces two principal tensile stresses.Therefore，the coordinatesand(tensile stress)of a point in the meridian(shown in Fig.4)indicate the frost resistance whilst-(compressive stress)indicates the compression resistance.

Thus，the compressive meridian in Fig.4 shows clearly thatandin the meridian decrease with the increase of-，which means that increasing of the preloading level leads to the decreasing of the frost resistance of concrete.On the other hand，-decreases whenandincrease，which suggests thatfreeze-thaw cycles decreasethecompressive resistance of concrete.Consequently，the coupling effect of freeze-thaw and compressive load causes the specimen to fail earlier.

Moreover，evolution of concrete failure surface［9］simultaneously occurs as the number of freeze-thaw cycles grows.The evolution trend of compressive meridian is shown in Fig.4，which also deteriorates the resistance of concrete to freeze-thaw cycles and compressive load.

In addition，there was no appreciable amount of scaling detected in all preloaded concrete prisms，regardless of the preloading level.The reason may be that preloading accelerates the initiation and propagation of cracking，but not scaling of concrete surface［16］.

2.1.2 Influence of w/c ratio

The w/c ratios of all specimens in this paper are 0.47，0.59，and 0.67.The tests conducted on non-air-entrained concrete with different w/c ratios showed different freeze-thaw responses.As shown in Fig.3，increasing the w/c ratio from 0.47 to 0.67 causes an appreciable change in the character of concrete.For instance，without preloading，the number of freeze-thaw cycles to failure for E-0.47 is more than 140，while the number is less than 100 and 60 for E-0.59 and E-0.69 respectively;when the stress ratio is 0.3，the number of freezethaw cycles at failure for E-0.67 is about 50%of the number for E-0.47.These results imply that for the same stress ratio，the higher the w/c ratio is given，the smaller the number of freeze-thaw cycles to failure is obtained.These can be explained from two aspects.

Firstly，in the aspect of resistance of concrete，E-0.47 is stronger than E-0.67，because the compressive strength and tensile strength of E-0.67 are lower than those of E-0.47.Secondly，the higher the w/c ratio is，the more the pore solution exists in concrete.And as more pore solution is frozen，according to Powers' static hydraulic pressure hypothesis［11，27，28］，the hydraulic pressure P caused by ice formation rises.Therefore，in the aspect of load effect，the hydraulic pressure caused by freeze-thaw cycles in E-0.67 is higher than that in E-0.47.These may explain why the number of cycles to failure for E-0.67 decreases.

In summary，w/c ratio isan importantfactorthat determines the properties of concrete under the damage of freeze-thaw with or without external load.

2.1.3 Influence of air entrainment

In Fig.3，for all of the stress ratios，the number of freezethaw cycles to failure for E-0.47A is higher than that for E-0.47，which means that E-0.47A has a higher resistance to freeze-thaw than E-0.47.This indicates the effectiveness of air entrainment in protecting the concrete from micro cracking［18］.According to Powers' static hydraulic pressure hypothesis［11，27，28］，the entrained air bubbles can shorten the approximate half distance()between pores or voids，so as to reduce the hydraulic pressure in matrix to the point where matrix damage and micro cracking are prevented.

In addition，the amount of air-entraining agent used in this experiment was relatively less compared with other literatures［17，18］，which may be the reason why E-0.47A did not suffer significantly more cycles than E-0.47.

2.2 Damage velocity ofconcrete under the simultaneous action of load and freeze-thaw cycles

2.2.1 Definition of damage velocity

As shown previously，the number of freeze-thaw cycles to failure decreases with increasing of preloading level.However，it is not evident from the previous results that the external load accelerates the damage velocity.The dominant factor of failure for the preloaded specimens in the experiments reported herein is compressive stress induced by external loads.

So，a specimen's compressive strength loss after freezethaw cycles becomes the main factor to determine whether the specimen fractures. For different preloading level，the compressive strength loss of the specimens needed to fail is different.For example，the specimens subjected to a preloading level of 80%need only 20%of compressive strength loss prior to failure;but，the specimens subjected to a preloading level of 50%have to lose 50% of their compressive strength before fracture.Meanwhile，the experimental results show that the specimens subjected to a preloading level of 80%need fewer freeze-thaw cycles to failure than the specimens subjected to a preloading level of 50%.In other words，for the specimens subjected to preloading levelof80%，they need less compressive strength loss and fewer freeze-thaw cycles to fail.That is to say，for higher level preloaded specimen，fewer freeze-thaw cycles lead to less compressive strength loss，which can't support that higher preloading level leads to higher damage velocity.

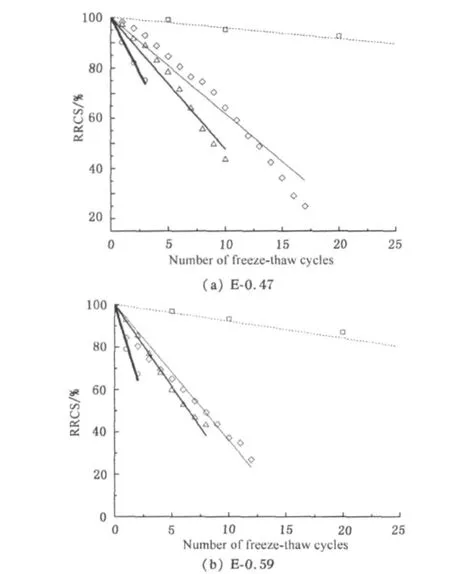
In order to understand the relationship between preloading level and damage velocity，the residual compressive strength(RCS)after each freeze-thaw cycle was recorded by ultrasonic impulse method with the formulas obtained in Table 2.The relative residual compressive strength(RRCS)is the ratio of the RCS value measured after each freeze-thaw cycle to that before the freeze-thaw cycling.Figure 5 shows the RRCS versus the number of freezing-thawing cycles for different stress ratios and different w/c ratios.As the number of freeze-thaw cycles increases，the RRCS of each specimen decreases.From Fig.5，it is apparent that the RRCS of specimens decreases sharply when stress ratio is over 0.The RRCS loss in one freeze-thaw cycle(designated Kss)can be defined as the damage velocity，which is the slope in the coordinate system.The bigger the absolute value of slope is，the more severe the damage is.So，Ksscan be obtained through the equation as follows:

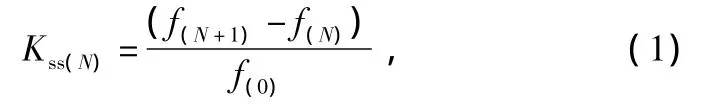
where，Kss(N)is the damage velocity after a certain number(N)of freeze-thaw cycles;f(N)is the RCS after a certain number(N)of freeze-thaw cycles;and f(0)is the initial compressive strength.

2.2.2 Average damage velocity

The experimentalresultsreported above (Fig.5)demonstrate that the damage velocity changes with the increase of freeze-thaw cycles.Most damage models［11，29，30］based on the Strain Equivalence Principle［31］focus on the variation of elasticity modulus.Since Young's modulus is not specifically related to strength for a material，the damage models can't be used to evaluate the evolution of strength under freeze-thaw.From the research of evolution of concrete failure surface under freeze-thaw condition［9］，itappearsthatthe compressive strength could decline approximately linearly with the increase of freeze-thaw cycles before ωc(related residual compressive strength)reaches 0.3，as shown in Fig.6.Consequently，in order to understand the effect of external loads on damage velocity，using the approach of linear regression on RRCS and freeze-thaw cycles to obtain the average damage velocity(Kass)is reasonable and necessary.

Fig.6 Predicted compressive strength comparing with experiment data of ordinary concrete

From comparison of the experimental results and regression analysis in Figs.7-9，the linear regression analysis is a good approach to derive the mathematical relationship between the RRCS and the number of freeze-thaw cycles.The linear regression analysis results are shown in Table 3.

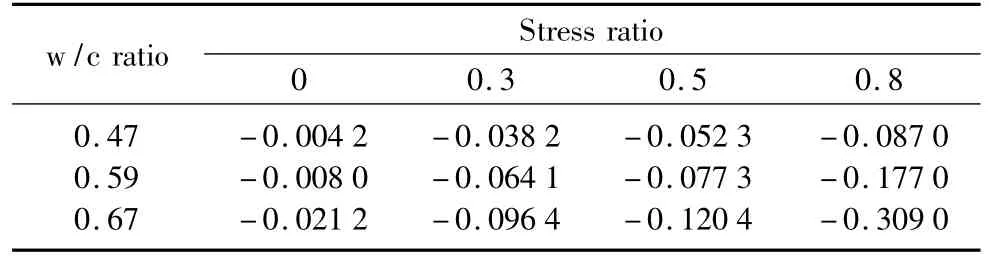
Table 3 Linear regression analysis results for Kass

2.2.3 Effect of external loads on average damage velocity

The RRCS of concrete subjected to different stress ratios(0，0.3，0.5，and 0.8)at different number of freeze-thaw cycles and the linear regression analysis models are given in Fig.7.The averaged damage velocities of the RRCS of all concrete prisms increase with increasing of the preloading level.Soit'sevidentthatthe externalloading acceleratesthe degradation process of concrete，which is exposed to freezethaw cycles regardless of w/c ratios.

From macroscopic perspective，the damage of concrete sufferingfreeze-thaw cycles and external loads is a very complex fatigue process.In this deterioration，the mechanical properties of concrete are determined by freeze-thaw damage，load damage，and the coupling effect，which aremore complicated and severe than those of the concrete under freezethaw damage only.Internal hydraulic pressure caused by freezethaw cycles is equally distributed tension in all directions.As concrete being compressed，the transverse strain due to the Poisson's effect is tensile strain，which can be added to the strain caused by internal hydraulic pressure to deteriorate the deterioration process.

At the mesoscale level，the compressive load can make the microcracks or microvoids in original concrete to grow and coalesce，which can reduce the load carrying capacityof concrete.So comparing with the same type concrete without being preloaded，the compressively preloaded concrete has lower strength and resistance.And，freezing and thawing also can decrease the strength and resistance of concrete.Therefore，the preloaded concrete can be considered as having initial freeze-thaw damage.Also，from some typical damage processes［11，16-18，30］，it is known that damage velocity increases as freeze-thaw cycles increases.As a result，preloaded concrete has higher damage velocity than the same type of concrete without preloading.

It can be concluded that external load can significantly raise the damage velocity of concrete exposed to freeze-thaw cycles.

2.2.4 Effect of w/c ratio on average damage velocity

Figure 8 shows the influence of w/c ratios on the damage velocities of the RRCS.It is found that the averaged damage velocity of RRCS increases as w/c ratio increases.

From Cai's model［11］，damage increment of concrete after per freeze-thaw cycle can be expressed as follows:

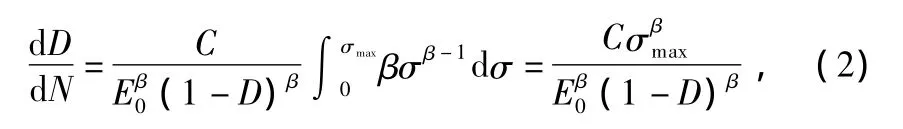
where，D is damage variable;N is the number of freeze-thaw cycles;C，β，and E0are material parameters for concrete;and σmaxis the maximum hydraulic pressure in freezing process.

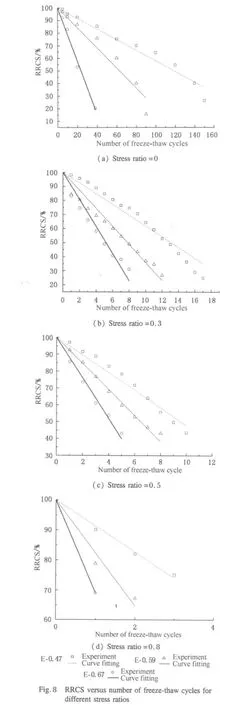
Formula(2)indicates that damage increment of concrete after per freeze-thaw cycle increases with the increase of the maximum hydraulic pressure.And from the previous definition，damage velocity is similar to damage increment in the aspect of describing the degradation velocity of concrete.Consequently，it can be derived that damage velocity increases as hydraulic pressure increases.According to Powers'static hydraulic pressure hypothesis［11，27，28］，also，higher w/c ratio causes more capillary pores in concrete，and more pore solution can be frozen to produce higher hydraulic pressure.As a whole，higher w/c ratio causes more severe damage of the RRCS of concrete in one freeze-thaw cycle.

Moreover，the higher the w/c ratio is，the lower the tensile strength is，which means concrete with higher w/c ratio has lower resistance to freeze-thaw cycles.Both of the previous analyses lead to the conclusion that the increasing of the w/c ratio causes an appreciable increase in the damage velocity of the RRCS.

2.2.5 Effect of air entrainment on average damage velocity

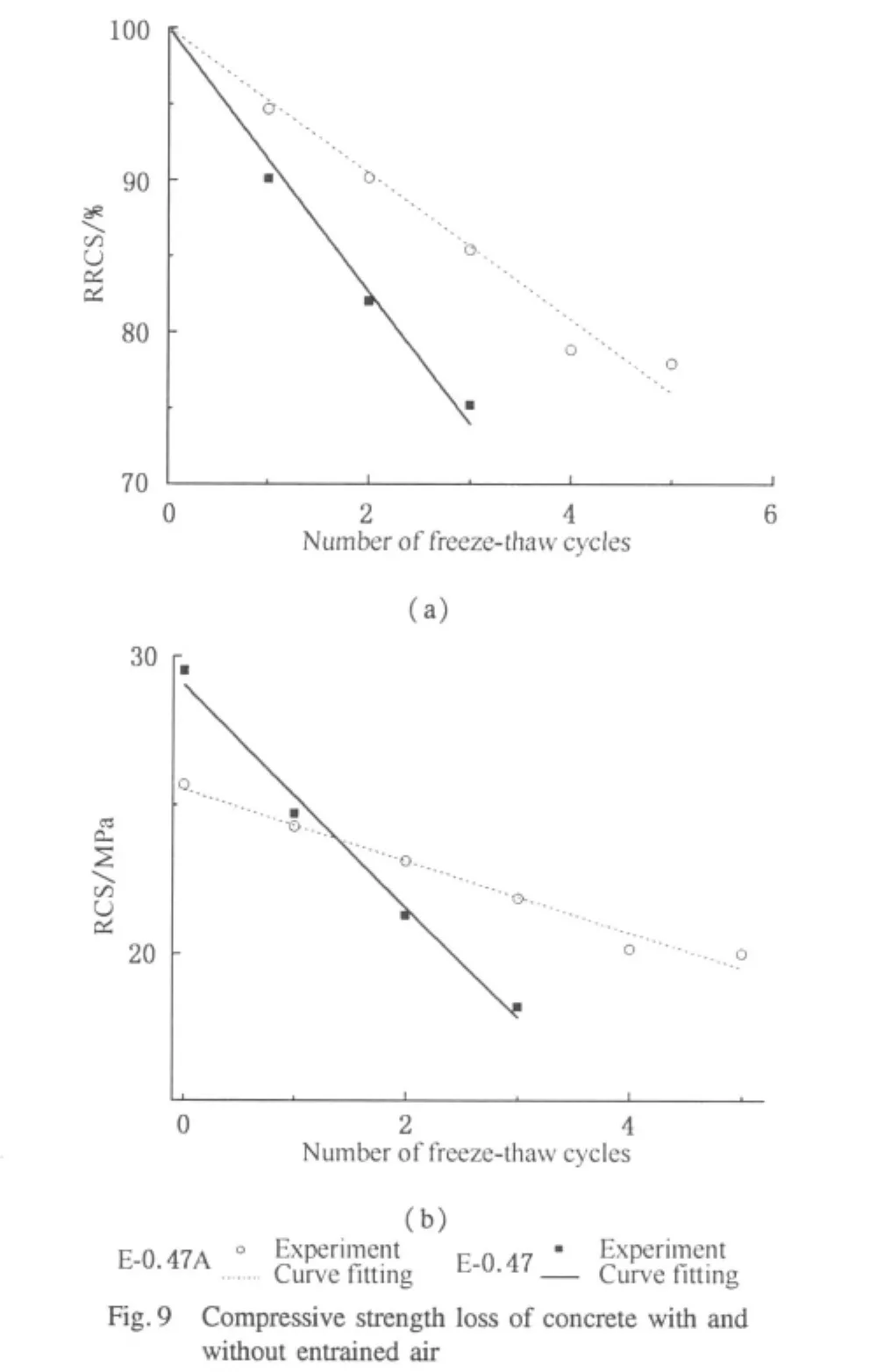
Figure 9 shows the RRCS and RCS versus number of freeze-thaw cycles for non-air-entrained concrete E-0.47 and air-entrained concrete E-0.47A at stress ratio of 0.8.As the number of freeze-thaw cycles increases，the RRCS and RCS of E-0.47A decrease at a slower rate than those of E-0.47.This may suggest that air entrained in concrete by air-entraining admixtures can slow down the damage velocity of freeze-thaw cycles and improve the frost-resistance of non-air-entrained concrete.However，it is noted that air-entrained concrete(E-0.47A)has a lower compressive strength than non-air-entrained concrete(E-0.47).Therefore，in practice，the w/c ratio needs to be reduced to guarantee the same strength.

3 Conclusions

Based on the results of this experimental investigation，the conclusion was drawn that the loss of compressive strength of concrete under the simultaneous actions of load and freeze-thaw cycles was more severe than that under the single frost action.External load could reduce the frost resistance of concrete significantly.With an increasing level of preloading，failure occured much earlier.The w/c ratio wasan important parameter，on which theporosity ofthe cementmatrix depended.Frost resistance increased rapidly with the decrease of the w/c ratio.As expected，air entrainment improved the frost resistance of non-air-entrained concrete despite of reducing the compressive strength of concrete.The failure surface of concrete and the evolution of failure surface were used in this paper to explain the external load's influence on frost resistance of concrete，while static hydraulic pressure hypothesis was used to explain the influence of w/c and air entrainment.

In this paper，the concept of damage velocity was defined.In order to understand the relationship between preloading level and damage velocity，the variable Kss(N)(RRCS loss in one freeze-thaw cycle)instead of the number of freeze-thaw cycles to failure was proposed to represent the damage velocity.The results indicated that the higher the preloading level or the w/c ratio was given，the higher the damage velocity of the RRCS of concrete was obtained.Also，air entrainment could decrease the damage velocity.The effect of external loads on average damage velocity was explained from both macroscopic perspective and mesoscopic perspective，while the effect of w/c ratio and air entrainment on average damage velocity were explained by static hydraulic pressure hypothesis and Cai's model.

［1］Mehta P K，Burrows R W.Building Durable Structures in the 21st Century［J］.Indian Concrete Journal，2001，75(7):437-443.

［2］Mehta P K.High-Performance Concrete Durability Affected by Many Factors［J］.Aberdeen′s Concrete Construction，1992，37(5):367-370.

［3］Mehta P K.DurabilityofConcrete-The ZigzagCourse of Progress［J］.Indian Concrete Journal，2006，80(8):9-16.

［4］Mather B.ConcreteDurability［J］. Cementand Concrete Composites，2004，26(1):3-4.

［5］Detwiler R J，Dalgleish B J，Brady R.Assessing the Durability of Concrete in Freezing and Thawing［J］.ACI Materials Journal(American Concrete Institute)，1989，86(1):29-35.

［6］Alexander M G，Magee B J.Durability Performance of Concrete Containing Condensed Silica Fume［J］.Cement and Concrete Research，1999，29(6):917-922.

［7］Moukwa M.Deterioration of Concrete in Cold Sea Waters［J］.Cement and Concrete Research，1990，20(3):439-446.

［8］Senbu O，Kamada E.Mechanism and Evaluation Method of Frost Deterioration of Cellular Concrete［C］.Durability of Building Materials and Components，Brighton，UK，1990:241-246.

［9］Tang G P.Research on Durability Evalution Methods of Concrete Structures under Freeze-Thaw Conditions［D］.Beijing:Tsinghua University，2006:39-56.(in Chinese)

［10］Cho T J.Prediction of Cyclic Freeze-Thaw Damage in Concrete Structures Based on Response Surface Method［J］.Construction and Building Materials，2007，21(12):2031-2040.

［11］Cai H.Prediction Model of Concrete Freeze-Thaw Durability［D］.Beijing:Tsinghua University，1998.(in Chinese)

［12］Richardson A，Coventry K，Bacon J.Freeze/Thaw Durability of Concrete with Recycled Demolition Aggregate Compared to Virgin Aggregate Concrete［J］.Journal of Cleaner Production，2011，19(2/3):272-277.

［13］Pospichal O，Kucharczykova B，Misak P，et al.Freeze-Thaw Resistance of Concrete with Porous Aggregate［C］.The 10th International Fatigue Congress，Prague，Czech Republic，2010:521-529.

［14］Graybeal B，Tanesi J.Durability of an Ultrahigh-Performance Concrete［J］.Journal of Materials in Civil Engineering，2007，19(10):848-854.

［15］Shang H S，Song Y P，Qin L K.Experimental Study on Strength and Deformation of Plain Concrete under Triaxial Compression after Freeze-Thaw Cycles［J］.Building and Environment，2008，43(7):1197-1204.

［16］Mu R，Miao C W，Luo X，et al.Interaction between Loading，Freeze-Thaw Cycles，and Chloride Salt Attack of Concrete with and without Steel Fiber Reinforcement［J］.Cement and Concrete Research，2002，32(7):1061-1066.

［17］Sun W，Zhang Y M，Yan H D，et al.Damage and Damage Resistance of High Strength Concrete under the Action of Load and Freeze-Thaw Cycles［J］.Cement and Concrete Research，1999，29(9):1519-1523.

［18］Zhou Y X，Cohen M D，Dolch W L.Effect of External Loads on the Frost-Resistant Properties of Mortar with and without Silica Fume［J］.ACI Materials Journal，1994，91(6):591-601.

［19］ASTM.ASTM C666/C666M-2003(2008)，StandardTest Method for Resistance of Concrete to Rapid Freezing and Thawing［S］.ASTM International，2003.

［20］ASTM.ASTM C671-94，Standard Test Method for Critical Dilation of Concrete Specimens Subjected to Freezing［S］.ASTM International，1994.

［21］Research Institute of Highway Ministray of Transport.JTGE30-2005，Test Method of Cement and Concrete for Highway Engineer［S］.Beijing:China Communications Press，2005.(in Chinese)

［22］AVICI. A Kind ofCorrosion-ProofStrain Gage:China，CN200620012079.0［P］.2007-06-06.(in Chinese)

［23］Trtnik G，Kavcic F，Turk G.Prediction of Concrete Strength Using Ultrasonic Pulse Velocity and Artificial Neural Networks［J］.Ultrasonics，2009，49(1):53-60.

［24］Prassianakis I N，Prassianakis N I.Ultrasonic Testing of Nonmetallic Materials:Concrete and Marble［J］.Theoretical and Applied Fracture Mechanics，2004，42(2):191-198.

［25］Sandor P.Analysis of the Concrete Strength Versus Ultrasonic Pulse Velocity Relationship［EB/OL］.2007.http://www.asnt.org/publications/materialseval/basics/feb01basics/feb01basics.htm.

［26］Chen W F，Saleeb A F.Constitutive Equations for Engineering Materials［M］.New York:John Whiley ＆ Sons Inc.，1982:263-288.

［27］Powers T C，Wills T F.The Air Requirement of Frost-Resistance Concrete［C］.Highway Research Board，Washington DC，USA，1949:184-202.

［28］Powers T C，Helmuth R A.Theoryof Volume Change in Hardened Porland Cement Paste during Freezing［C］.Highway Research Board，Washington DC，USA，1953:285-297.

［29］Wei J，Wu X H，Zhao X L.A Damage Model of Concrete under Freeze-Thaw Cycles［J］. JournalofWuhan Universityof Technology-Materials Science Edition，2003，18(3):40-42.

［30］Løland K E.ContinuousDamage ModelforLoad-Response Estimation of Concrete［J］.Cement and Concrete Research，1980，10(3):395-402.

［31］Lemaitre J.A Course on Damage Mechanics［M］.Berlin，Germany:Springer，1992:11-15.