小型控制力矩陀螺扰动建模及性能指标分析

张尧 金磊 徐世杰

（1 北京理工大学宇航学院，北京100081）（2 北京航空航天大学宇航学院，北京 100191）

1 引言

目前的遥感卫星以及侦察卫星为能实现星上光学有效载荷的成像时间和成像精度要求，需要星本体在快速机动过后具有快速稳定的能力。国外许多先进的卫星都具备快速姿态机动与快速稳定的性能，如美国商业卫星WorldView 系列以及高级KH－11可见光成像侦察卫星等［1］。

对于这类具有快速机动快速稳定能力的卫星，常使用的星上执行机构是控制力矩陀螺（CMG），它能够提供较大的力矩输出且对空间环境无污染［2－3］。但是由于CMG 转子在加工中产生的静动不平衡以及机械轴承的生产缺陷使其成为了星上重要的振动源之一，将直接影响星体的姿态精度和稳定度［4］。为了能够满足光学有效载荷的成像精度要求，需要重点分析控制力矩陀螺这种扰动源的扰动特性，并能够根据任务要求提出CMG 的性能指标约束。

在扰动建模方面，多集中在对飞轮的研究上，如Melody采用与哈勃望远镜相同的机械轴承飞轮，通过大量试验建立了飞轮干扰的经验模型和分析模型［5］；Masterson等在Melody所建立的飞轮扰动模型的基础上，建立了Ithach B和Ithaco E类型飞轮的扰动模型。这些飞轮经验模型和分析模型在后来的飞轮扰动对载荷抖动的影响分析以及飞轮隔振系统设计中得到了广泛的应用［6］，如：高等X 射线天体物理设备、航天空间干涉仪任务、太阳动态观测任务、詹姆斯韦伯望远镜、GONES－N 航天器、类地行星探测器等［7－10］。国内也有一些学者在飞轮扰动的解析动力学模型和经验模型中幅值系数的计算上做了一定的贡献［11－14］。

然而，目前对CMG 的扰动解析模型、它的各项扰动对整星姿态精度和稳定度的影响分析以及如何提出满足星体姿态精度和稳定度要求的CMG 设计指标的研究很少。本文将对CMG的各项扰动进行深入细致地研究分析，得出含有CMG 扰动的精确的整星动力学模型，从而根据任务要求提出CMG 的性能指标以指导工程设计，这将对中国遥感卫星的实现具有实际的工程意义。

2 含有扰动项的星载CMG 动力学模型

2.1 坐标系以及扰动描述

为描述系统各体之间的相对运动，首先定义如下坐标系：惯性坐标系fe（Oexeyeze），固定在惯性空间中；星本体坐标系fb（Obxbybzb），固定在星本体上，Ob为星体的质心；CMG 的框架坐标系fg（Ogxgygzg），是框架固联坐标系，Og为框架质心，zg沿框架轴方向，xg与zg垂直，位于框架平面内且与转子几何轴在Ogxgyg平面上投影的夹角最小，yg满足右手法则；CMG 的框架参考坐标系fg0（Og0xg0yg0zg0），是非自旋坐标系，Og0为框架质心，zg0沿框架轴方向，xg0沿xg轴初始方向，yg0满足右手法则；转子准几何体坐标系ff（Ofxfyfzf），是非自旋坐标系，Of在转子几何中心上，xf沿转子几何轴，由于转子轴承是机械式的，因此可认为是刚性支撑，转子几何轴与轴承重合。当不考虑轴承安装偏差等的影响下，ff与fg一致，当考虑轴承安装偏差时，需要小角度欧拉旋转使两者重合。Og到Of的矢径rfg表征了转子轴与框架轴的不相交，ff与fg之间的旋转角度表征了转子轴与框架轴的不垂直；转子几何体坐标系fw（Owxwywzw）是转子固联坐标系，随转子高速旋转，Ow即Of在转子几何中心上，而xw与xf重合，初始状态下，fw与ff一致；转子惯量主轴坐标系fI（OIxIyIzI），随转子转动，OI为质心，其与Ow之间的矢径ρw表征了转子的静不平衡，fI（OIxIyIzI）和fw（Owxwywzw）之间的旋转角度表征了转子的动不平衡。

记rxy是从Oy到Ox的矢径，Axy是从坐标系fy到fx的坐标转换矩阵，其中下标x 和y 可表示任意上述坐标系。下文中的坐标系之间的矢量关系以及坐标转换关系均采用这种通用表达。

在fw中记转子的静不平衡量ρw＝［γ ξ ζ］T。γ、ξ和ζ 分别是由于加工误差造成的质心偏移小量。转子的动不平衡量可表示为

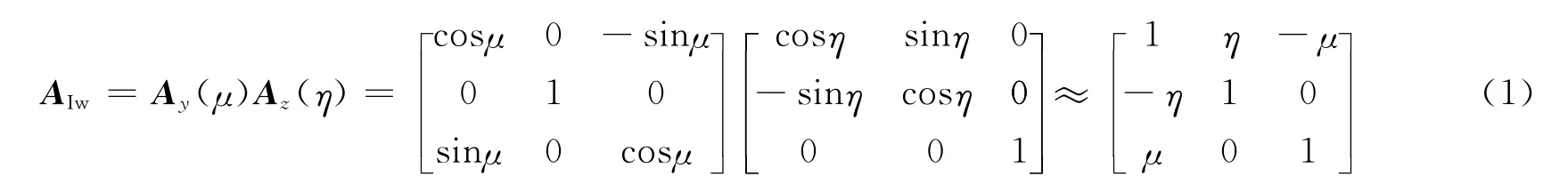
式中 Ay（μ）表示绕坐标轴y 轴旋转一个小角度μ；Az（η）表示绕坐标轴z轴旋转一个小角度η。

在fI中，记转子相对于质心的惯量矩阵为＝diag（IwIxIwIyIwIz），其中的上标“OI”表示该惯量矩阵表示在转子惯量主轴坐标系下。下文中类似表达的上标均是用来表示该矩阵被描述在某个坐标系下。姿控用转子采用“I”形圆盘结构［15］，即IwIx＞IwIy＝IwIz，则根据坐标转换以及转动惯量的移心定理，可得到在fw中，由于存在转子静动不平衡因素，则转子相对于几何中心的惯量矩阵IOfww可表示为

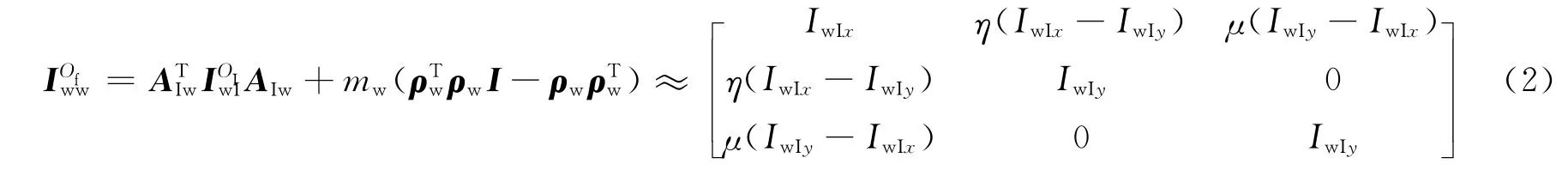
转子轴与框架轴的不垂直可由坐标系fg到转子准几何体坐标系ff的坐标转换矩阵表示为

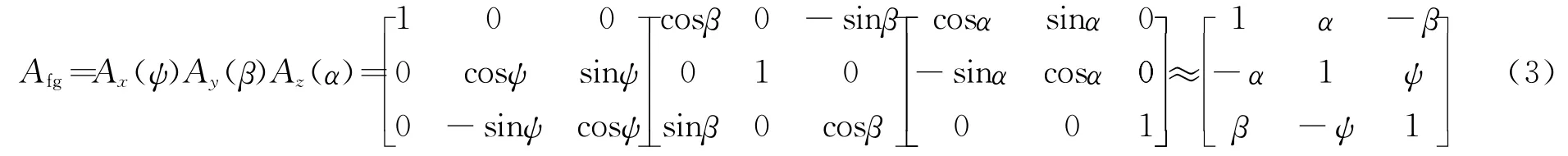
式中 Ax（ψ）表示绕坐标轴x旋转一个小角度ψ；Ay（β）表示绕坐标轴y旋转一个小角度β；Az（α）表示绕坐标轴z旋转一个小角度α。

2.2 星载CMG 动力学模型

记rw是从Of（或Ow）到转子上任意一点的矢径，rg是从Og到框架上任意一点的矢径。则转子上任意一点相对惯性系的矢径rwe和框架上任意一点相对惯性系的矢径rge可分别表示为

由式（4）分别求得转子的动量和角动量，并将其表示在框架坐标系中，可得到

式中 上标“×”表示单位矢量列阵的反对称斜方阵；vb和ωb分别是星体固连坐标系原点的绝对速度和绝对角速度；是框架相对星体的转动角速度；Ω＝［Ω 0 0］T，Ω 是fw相对于ff的角速率（转子转速）；mw是转子质量。

由式（5）可进一步求得框架的动量和角动量，并将其表示在框架坐标系中：

式中 mg是框架的质量；Ig是框架的惯量。

根据式（6）～（9），在框架坐标系fg下，整个CMG 的绝对动量以及相对于框架坐标系原点Og的动量矩可以表示为

利用动量矩定理可以得到CMG 转动动力学方程为

式中 TQg是CMG 所受到的外力矩；vgg为在fg下表示的框架几何中心绝对速度；ωgg为在fg下表示的框架绝对角速度。分别表示为

将式（10）、式（11）、式（13）和式（14）代入式（12）中可得到考虑了框架的惯量特性，转子静、动不平衡，框架轴与转子轴不垂直且不相交的完整星载CMG 动力学方程。

同样利用动量定理也可以得到CMG 平动动力学方程为

式中 FQg是CMG 所受到的外力矩。将式（10）和式（14）代入式（16）即可得到CMG 平动动力学方程的具体表达式，这里不再详细给出。

2.3 星载CMG 动力学模型分析

传统的飞轮经验模型一般仅包含扰动力和扰动力矩的求取［5］：

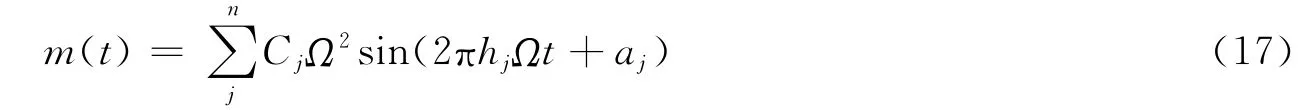
式中 m（t）是扰动力或力矩；n是该模型中包含的谐波数；Cj是第j个谐波的振幅，单位为N2／Hz；Ω 是飞轮转速，用Hz表述；hj是第j 个谐波的谐波数；aj是随机相位（假定在0～2π均匀变化）。

该飞轮扰动经验模型的得到要充分依赖于试验数据，通过试验数据对各谐波数下的扰动幅值进行求解，得到飞轮总的扰动力和扰动力矩。该模型对于地面试验仿真验证具有一定的指导作用。但是同本文所建立的星载CMG 精细动力学模型相比，该扰动模型不具有表达同星体或者其他部件的耦合特性的能力，并且不利于搭建整星系统级软件仿真模型。

本文所建立的星载CMG 精细动力学模型主要关注的是转子静动不平衡以及安装误差等因素。为能和飞轮扰动的经验模型进行对比，暂且不考虑CMG 的安装误差，并且通过忽略高阶小量。可以由式（15）、（16）简化得出由转子静动不平衡引起的扰动力Fdw和扰动力矩Tdw在CMG 转子坐标系下的解析表达式：

由式（18）、（19）可知：由转子静动不平衡引起的扰动力和扰动力矩是和转子同频，并且幅值和转子转速的平方成比例的，由转子静不平衡引起的扰动力的比例系数由转子动不平衡引起的扰动力矩的幅值系数根据文献 ［5，12－13］的经验模型得知，转子静动不平衡引起的扰动力和扰动力矩的频率特性以及幅值特性都和上述一致。由此可得知，本文所建立的星载CMG 精细动力学模型中包含了转子静动不平衡引起的扰动力和扰动力矩，同经验模型相比，该模型还包含了安装误差、CMG 部件之间以及同星体之间的耦合特性。但是，本文仅考虑了CMG 的转子静动不平衡以及安装误差因素，在实际工程应用中，CMG 扰动还包含了转子轴承、电机等的扰动项。这些扰动项可以借助经验模型中的对应谐波扰动纳入到本文所建立的精细动力学模型中，并对高精度高稳定度航天器进行前期理论论证和分析。

其次，对所建立的CMG 动力学模型进行数值仿真验证，对CMG 转子电机和框架电机均使用工程上易于实现的双闭环调速控制系统。为能对含有各扰动项情况下CMG 输出力矩进行仿真验证及分析，则先对各扰动量进行赋值。CMG 转子静不平衡量ρw＝［0.8 1.0 0.8］T（单位μm）；CMG转子动不平衡量η＝5.882 4×10－6rad，μ＝8.823 5×10－6rad；转子轴与框架轴不相交量rfg＝［6 8 8］T（单位μm）；转子轴与框架轴不垂直量α＝β＝ψ＝0.000 1rad［16］。当理想框架角速度输入为˙δ＝sin（0.5t）（°）／s，转子转速为6 000r／min时，不加入任何扰动和加入各项扰动下的有效输出力矩时域仿真结果如图1所示。

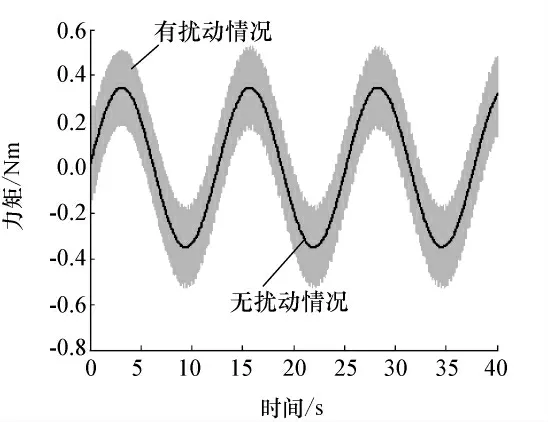
图1 有无扰动情况下CMG 输出力矩对比Fig.1 Output torques of the CMG with disturbances and without disturbances

由图1可知，不加任何扰动的时候，CMG 的输出力矩能力约为0.35Nm，当加入转子静动不平衡量以及安装误差量等各项扰动时，输出力矩产生较大的振动，该振动将对星体产生一定的影响。为能更确切地分析扰动频率特性，结合图1的仿真数据，绘制输出力矩频谱图，如图2所示。

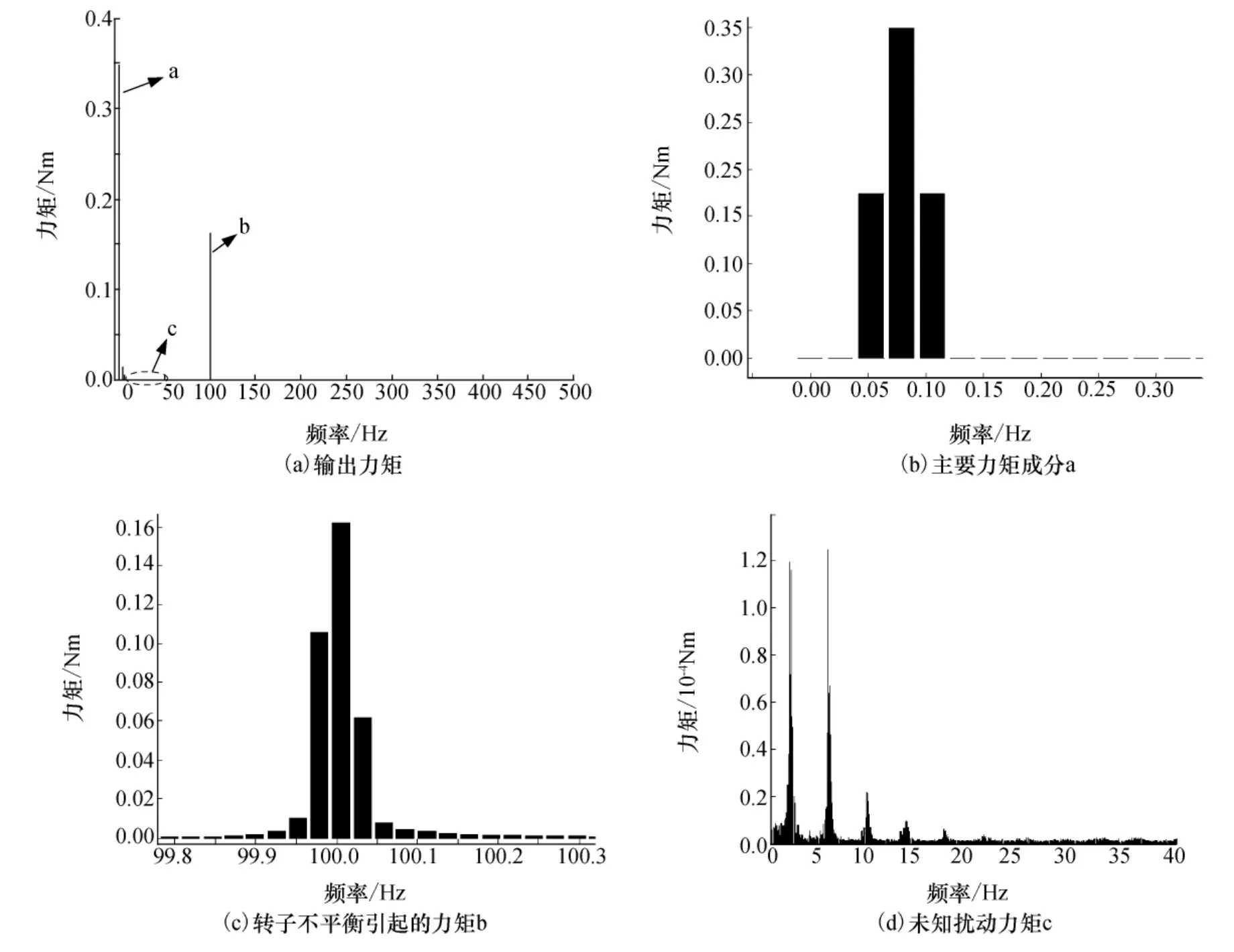
图2 CMG 带有扰动的输出力矩频谱Fig.2 Spectrogram of output torque of the CMG with disturbances

由图2可以得知，输出力矩测量值幅值谱中低频力矩是CMG 的主要输出力矩，它对应的频率大小与框架转动频率相同，它的幅值大致为0.35Nm，这和时域仿真结果相一致。而CMG 的输出力矩中包含高频扰动力矩，对应的频率在CMG 转子转动频率100Hz附近。高频扰动的幅值大致为0.16Nm，该扰动主要是由和转子转速同频的转子动不平衡引起的，并且该影响量是正常输出力矩的45.7%，可见动不平衡的影响较大。中低频段的扰动主要是由转子和框架伺服控制系统以及安装误差引起的，幅值很小，约为10－4Nm 的量级以下，在对星体姿态精度和稳定度要求不是很高的情况下，可忽略不计。

由以上仿真结果可以得知，本文所重点考虑的由转子静动不平衡引起的扰动频率和转子同频，属于高频扰动。在航天器姿态控制回路中，由于CMG 响应能力有限，这种高频扰动将直接传递给星体，引起星体的振动，造成星上所携带的光学有效载荷成像品质下降。

3 CMG 扰动对整星姿态精度和稳定度影响分析

3.1 含有CMG 的整星动力学模型

星体上任意一点相对惯性系的矢径r为

式中 rb是从Ob到上平台上任意一点的矢径。根据式（4）、式（5）和式（20）可分别求得在星体坐标系下描述的CMG 转子、框架以及星体的动量和相对于Ob的动量矩，具体表示为

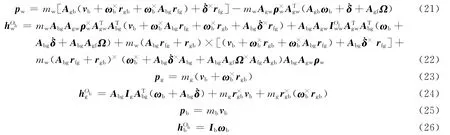
式中 mb和Ib分别是星体的质量和惯量。假设卫星带有m 个CMG，用i表示第i个CMG。根据式（21）～（26），整星（包括控制力矩陀螺）在fb中表示的动量和相对于Ob的动量矩可以表示为

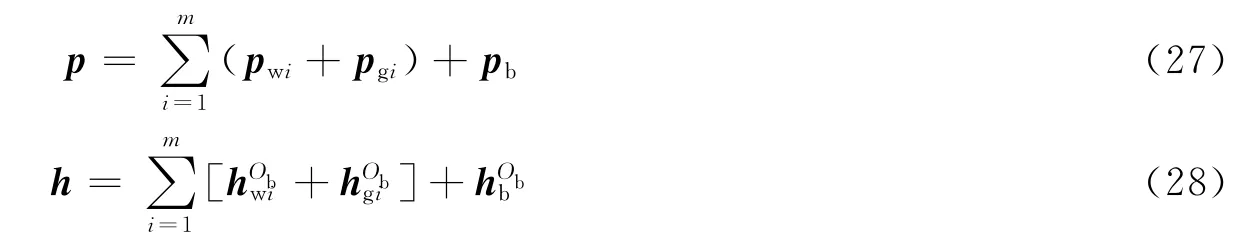
分别利用动量矩定理和动量定理可以得到整星的转动动力学方程和平动动力学方程，具体表示为

式中 Td为外界环境干扰力矩；Fd为外界环境干扰力，不包括万有引力项。将式（21）～式（26）分别代入式（29）、（30）可得整星动力学方程的展开式，由于表达形式较为复杂，这里不再列写。

3.2 CMG 性能指标分析

扰动的主要来源是转子的不平衡量，动不平衡产生扰动力矩，而静不平衡产生扰动力。这些扰动将直接影响星体姿态精度和稳定度，为能够设计出充分满足星体精度和稳定度要求的小型CMG，则需要对CMG 进行重要参数的上限分析，以期为CMG 的工程化设计提出要求。

整星姿态控制器选用工程易于实现的PID 控制器，暂时忽略姿态测量环节和环境干扰。初始角度为1.5°，完成姿态稳定控制。分别对不同静动不平衡量情况下进行仿真，得到表1～表3的结果。其中，表1令静不平衡量为ρw＝［0.8 1.0 0.8］T（单位μm）不变；表2令动不平衡量η＝5.882 4×10－6rad，μ＝8.823 5×10－6rad不变。

表1 静不平衡量不变，动不平衡量对姿态影响Tab.1 Influence of the dynamic imbalance on the attitude precision and stability when the static imbalance does not change

表2 动不平衡量不变，静不平衡量对姿态影响Tab.2 Influence of the static imbalance on the attitude precision and stability when the dynamic imbalance does not change

表3 静动不平衡量对姿态影响Tab.3 Influence of the static and dynamic imbalance on the attitude precision and stability

一般来说，星体要求的姿态精度为0.01°（36″），稳定度为1×10－4～5×10－4（°）／s（0.36～1.8（″）／s）。从表1～表3中得知，动不平衡量需要在10－5rad量级或者更优才能达到指标要求；静不平衡量需要在100μm量级或者更优才能达到指标要求。因此，对于CMG转子的静动不平衡量可以初步确定满足指标要求的限定值为：CMG转子静不平衡量ρw≤ ［0.8 1.00.8］T×10－4m；CMG 转子动不平衡量η≤5.882 4×10－5rad；μ≤8.823 5×10－5rad。

但是为能够使得CMG 引起的扰动力较小，则转子静不平衡量需要取到较小值，可以取静不平衡量为微米量级，这是目前国外可以达到的量级。因此可得，CMG 转子静不平衡量不大于1.15g·cm、CMG 转子动不平衡量不大于17g·cm2可以充分满足系统稳定性要求。

其他仿真参数以及条件不变，选用CMG 转子静不平衡量是1.15g·cm、CMG 转子动不平衡量是17g·cm2情况下，分别选取不同的CMG 框架电机角速度测量精度，可得星体姿态精度和稳定度如图3、图4所示。

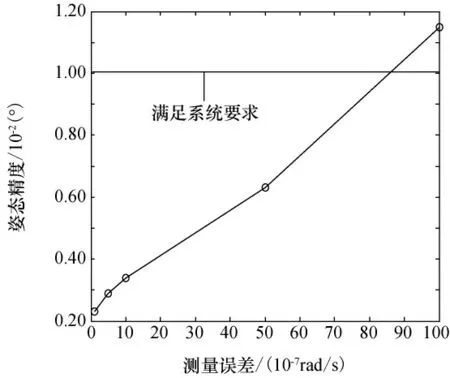
图3 框架角速度测量误差对星体精度的影响Fig.3 Influence of the measurement error of the CMG′s gimbal angular velocity on the attitude precision

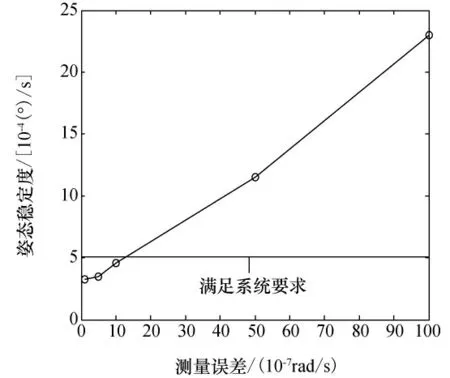
图4 框架角速度测量误差对星体稳定度的影响Fig.4 Influence of the measurement error of the CMG′s gimbal angular velocity on the attitude stability

由图3和图4可知，如若星体要求的姿态精度为0.01°，稳定度为1×10－4～5×10－4（°）／s，则在CMG 扰动存在的情况下，框架测量误差应该低于1.2×10－6rad／s量级才能同时满足姿态精度和稳定度的要求。

4 结束语

本文建立了星载CMG 的精细动力学模型，并和飞轮扰动的经验模型进行对比，分析了所建立动力学模型的正确性，并进行了扰动项对输出力矩影响的时域频域仿真分析验证。得知转子安装误差的影响较小，在对星体姿态精度和稳定度要求不是很高的情况下，可忽略不计。而由转子静动不平衡引起的扰动较大。此外，本文还建立了含有CMG 各项扰动的整星动力学模型，并在整星姿态控制系统仿真中得知，为能达到姿态精度为0.01°、稳定度为1×10－4～5×10－4（°）／s的星体要求，CMG 转子静不平衡量应小于1.15g·cm、动不平衡量应小于17g·cm2，框架测量误差应小于1.2×10－6rad／s量级。这些性能指标的约束能够给CMG 的工程设计提供依据。但是，本文在讨论中忽略了CMG 其他部件的振动特性、太阳翼驱动机构以及太阳翼自身的低频振动特性，因此在以后的工作中，需要综合考虑星上各振动部件特性，根据任务要求，提出各振动部件的设计约束条件，如果还不能满足系统要求，则需要考虑对各振动部件进行振动控制问题研究。

［1］ROSER X，SGHEDONI M.Control Moment Gyroscopes and Their Application in Future Scientific Mission［C］.Processing of the 3th ESA International Conference on Spacecraft Guidance，Navigation and Control Systems，1996：523－528.

［2］WIE BONG.Singularity Escape／Avoidance Steering Logic for Control Moment Gyro Systems［J］.Journal of Guidance Control and Dynamics，2005，28（5）：948－956.

［3］JIN LEI，XU SHIJIE.An Improved Constrained Steering Law for SGCMGs with DPC ［J］.Acta Mechanica，2009，25（5）：713－720.

［4］MASTERSON REBECCA A，MILLER DAVID W，GROGANT ROBERT L.Development of Empirical and Analytical Reaction Wheel Disturbance Models［C］.The 40th AIAA／ASME／ASCE／AHS／ASC Structures，Structural Dynamics，and Materials Conference，St.Louis，MO，Apr.12－15，1999.

［5］MELODY J W.Discrete－Frequency and Broadband Reaction Wheel Disturbance Models［R］.JPL Interoffice Memorandum，June 1，1995.

［6］MASTERSON REBECCA A，MILLER DAVID W.Development and Validation of Empirical and Analytical Reaction Wheel Disturbance Models［D］.Cambridge：Massachusetts Institute of Technology，1999.

［7］LIU KUOCHIA，MAGHAMI PEIMAN.Reaction Wheel Disturbance Modeling，Jitter Analysis，and Validation Tests for Solar Dynamics Observatory［C］.AIAA Guidance，Navigation and Control Conference and Exhibit，August 18－21，Honolulu，Hawaii，2008.

［8］WECK OLIVIER L，MILLER DAVID W.Integrated Modeling and Dynamics Simulation for the Next Generation Space Telescope ［C］.UV，optical，and IR space telescopes and instruments，Proceedings of the Conference，Munich，Germany，Mar.29－31，2000：920－934.

［9］MILLER SCOTT E，KIRCHMAN PAUL，SUDEY JOHN.Reaction Wheel Operational Impacts on the GOES－N Jitter Environment［C］.AIAA Guidance，Navigation and Control Conference and Exhibit，Hilton Head，South Carolina，August 20－23，2007.

［10］LOBOSCO DAVID M，BLAUROCK CARL，CHUNG SOONJO，et al.Integrated Modeling of Optical Performance for the Terrestrial Planet Finder Structurally Connected Interferometer［C］.Proceedings of SPIE，SPIE－5497，2004：278－289.

［11］孙杰，赵阳，田浩.改善航天器反作用轮扰动实验模型参数的辨识方法 ［J］.空间科学学报，2006，26（1）：70－74.SUN JIE，ZHAO YANG，TIAN HAO.Identification Method to Improve Disturbance Model Parameters of Reaction Wheel［J］.Chinese Journal Space Science，2006，26（1）：70－74.

［12］孙杰，赵阳，王本利.航天器反作用轮扰动精细模型 ［J］.哈尔滨工业大学学报，2006，38（4）：520－522.SUN JIE，ZHAO YANG，WANG BENLI.Development of Precise Disturbance Model of Reaction Wheel Assembly on a Spacecraft［J］.Journal of Harbin Institute of Technology，2006，38（4）：520－522.

［13］王全武，虎刚.飞轮振动频谱特征的初步理论分析和验证［J］.空间控制技术与应用，2008，34（4）：42－46.WANG QUANWU，HU GANG.Analysis and Validation of Flywheel Vibration Spectrum Characteristics［J］.Aerospace Control and Application，2008，34（4）：42－46.

［14］邓瑞清，虎刚，王全武.飞轮和控制力矩陀螺高速转子轴向干扰特性的研究 ［J］.航天控制，2009，27（4）：32－36.DENG RUIQING，HU GANG，WANG QUANWU.Axial Disturbance Characteristics for High Speed Rotor of Flywheel and CMG ［J］.Aerospace Control，2009，27（4）：32－36.

［15］金磊，徐世杰.带有两个飞轮的欠驱动航天器姿态稳定控制研究［J］.中国空间科学技术.2009，29（2）：16.JIN LEI，XU SHIJIE.Attitude Stabilization of an Underactuated Spacecraft with Two Reaction Wheels［J］.Chinese Space Science and Technology.2009，29（2）：16.

［16］金磊.使用角动量交换装置的航天器姿态动力学与控制问题研究 ［D］.北京：北京航空航天大学，2008.JIN LEI.Study on Attitude Dynamics and Control of Spacecraft Using Angular Momentum Exchange Devices［D］.Beijing：Beihang University，2008.