一种基于层次化社团结构的网络可视化方法

谈煜，梁润鹏

0 引言

大型网络的可视化面临3个主要问题：第一是如何对节点进行合理的布局。为此，需要保证节点布局的均匀性、对称性和美观性[1]，要尽量避免网络中不相关节点之间的重叠，同时要保证联系紧密的节点之间位置尽量靠近。二是在展现网络整体结构的同时又不遗漏重要的局部信息。复杂网络的规模巨大，信息繁多，所以从整体上对网络的结构有一定的了解是十分必要的，而有些局部信息能对网络的形成和演化起到重要作用，因此也必须予以保留。三是要体现网络的层次化特性。对于大型网络，由于其规模庞大，如果直接对网络进行可视化，用户很难从可视化效果中观察出有用信息，因此将网络划分为层次化社团结构再进行可视化是非常必要的。

网络可视化领域中最常用的布局算法是力导引算法，该方法最早由Eades于1984年提出[2]。力导引算法不受网络自身性质的限制，且产生的布局效果对称美观，但是由于其复杂度较高而无法适用于大规模网络。后来，在力导引算法的基础上产生了多尺度（multiscale）方法[3]以及FADE方法[4]等改进，这些方法都采用了图划分的思想，提高了处理速度和处理数据的规模，但由于他们的划分方法只是将网络简单的拆分为子图，从而很难体现网络本身的特性。

基于上述考虑，本文提出了一种基于层次化社团结构、力导引算法、局部环形布局算法并可以应用于大型网络的快速可视化方法，用 JAVA 语言编程对其加以具体实现。层次化社团结构[5]是指网络中相互连接紧密的节点形成一些小规模的社团，而这些较小的社团再结合成较大的社团，如此依次向上聚合，形成具有层次性的结构。针对上面所提到的3个问题，本文提出的方法都做了相应的考虑。

此外，本文提出的方法可以利用阈值调节来完成力学模型算法和环形布局算法的切换，从而可以使用户根据处理不同网络数据的需要进行自由选择，提高了方法的通用性和便捷性。

1 方法的基本思想

当前主流的可视化软件和工具大多都提供了力学模型算法进行布局，而力导引算法的局限性导致了它们不适用于较大规模数据的处理。首先采用了 Blondel[5]快速算法对网络进行处理，将网络划分成多个层次的不同社团，然后依次在每一层次分别使用力导引算法，最后再在同一平面上将整个网络展示出来，如图1所示：

图1 Blondel快速算法的处理过程示例，可以看到每次循环中，首先通过模块度优化得到相应社团，再将属于同一个社团的节点或子社团合并成更大的社团(取自文献[5])

选择的力导引算法是FR算法[6]，该算法虽然只适用于较小规模的网络，由于事先已经将网络划分成社团结构，并将社团视为节点进行处理，而社团的数目比节点的数目要小的多，这样就大大提高了处理效率，从而能够较好地处理大规模网络。

而在社团划分算法的选择上，选择Blondel快速算法。选择 Blondel快速算法的主要原因有两个：第一，Blondel快速算法是基于大规模网络数据的社团划分算法，在已有社团划分算法中是速度最快的方法之一；第二，Blondel快速算法可以将网络划分为多个层次，这样有利于将原网络分为几个层次分别处理，加快了数据处理速度。

为了能够更好地将力导引算法和社团方法结合起来，必须要对原来的FR算法的一些参数进行修改。在原文献中，显示区域设置为矩形，这样做的目的其实是为了能够最大程度的占用电脑屏幕空间。方法中，由于需要在每个层的每个社团中使用布局算法，将显示区域设置为圆形，以方便对原网络的层次化处理。同时，原方法中的引力和斥力系数 K的定义为：

其中，为常数。而在我们的方法中，K定义为：

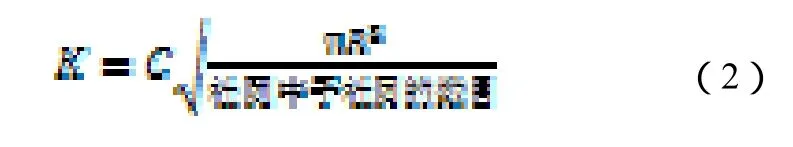
其中，R为社团的半径大小。

假设Blondel算法将网络从低到高划分成N层，上一层中的社团包含下一层之中的社团，以此类推。这样，第 N层为最低的一层，即为网络中每个节点所在的层，第1层为最高的一层。在这个方法中，需要在第1层上再加一层，这一层之中只有一个社团，即为整个网络，视作第0层。在此基础上，从N-1层开始，由低到高依次对每层中的每个社团内部的社团（或节点）使用弹簧算法，直到第0层为止。

为了使社团中的子社团不超过以该社团半径 R为半径的圆形显示区域，在力导引布局的过程中，如果某次节点位置更新使得子社团的半径到圆心的距离超过了R-r(r为子社团自身的半径)，则将子社团强制移动到距离圆心半径 R-r的位置，如见图2、图3所示：

图2 子社团在力导引算法布局过程中

图3 社团半径取法示意图

为了更好地应对层次化处理方式，可对于每个社团或节点，都定义了一个半径值，这个值实际上就是最终可视化结果中每个社团或节点的显示区域。对于最低层（第 N层）的节点，事先定义好节点的半径（常数），第N-1层开始直到第 0层，每层中每个社团的半径取决于它所包含的子社团。采用的计算公式如下：

事实上，这样的计算方法往往会导致显示区域过大，从而使整个可视化效果中节点显得过于稀疏。根据对实际数据的处理经验，这种情况对于越高的层越明显。我们也提出了另一种社团半径的定义方法：

这个公式在一定程度上可以改善显示区域过大的问题。一般而言，在第 N层可以采用第一种半径定义方法，而在比较高的层则采用公式（4）所定义的半径。此外，我们也使用了一种另一种较为简单却有效的方法，即在公式（3）和公式（4）定义的基础上，不同层中的社团半径乘以一个不同的大于0且小于1的系数。一般而言，越高的层乘以的系数越小，这样可以有效的减少因为子社团半径简单相加而造成的显示空间浪费。

3 基于力导引算法的改进

以上即为提出方法的基本思想，但是对实际网络数据的处理经验显示，如果仅仅对网络这样处理，可视化效果并不理想，尤其对大规模网络而言。

首先要对FR算法中定义的斥力和引力进行改进。力导引算法原本是用于处理非层次结构的小规模网络的，特别地，网络中的每个节点大小都一致。而对于层次化结构，由于同一层中每个社团的大小都不尽相同，而且不同层的显示区域大小差别巨大，往往都是差一个数量级的，导致原来的斥力引力已经不合适，这也是可视化效果中节点、社团分布不均匀的一个重要原因。

为了使FR算法更加适应层次化结构，分别对斥力和引力的作用范围做了限定。为了使社团或节点间的重叠尽量减少，当社团或节点过于靠近或者已经有重叠时，需要让它们之间的引力消失。因此，将社团之间引力的作用范围设置为：，其中，和分别为社团A和B的半径大小。这样，当A和B重叠时，它们之间将只有排斥力而没有吸引力，如图4所示：

图4 排斥力的作用范围示意图

为了使社团或节点之间的排斥力不致过大，同时对某些稀疏网络可以节约一些处理时间，采用了类似于N-body问题[7]的方法。将斥力的作用范围设置为：，其中，和分别为社团A和B的半径大小。这样，当A和B之间的距离超过它们半径和的两倍时，它们之间将只有吸引力而没有排斥力，如图5所示：

图5 吸引力的作用范围示意图

通过这种限定，可以提高力导引算法在节点布局均匀方面的效率。

以上对斥力和引力作用范围的限定还有另外一个好处。可以看出，在进行FR算法布局的过程中，大部分社团或节点之间都只有一种力作用，这样可以使节点或社团位置变化的幅度更小，从而在一定程度上避免了布局时图的结构出现较大的波动，从一定程度上保证了布局的稳定性。

对非加权网络而言，在节点之间最多只有一条边连接。而通过Blondel快速算法得到的多层社团结构中，每层中的社团之间可能存在多条边连接，也就是说，从第N-1层到第0层，处理的图已经是加权网络。相应的，需要在模型中体现加权连边的存在。在原FR算法中，节点间引力的定义为：

其中，表示节点间的距离，表示节点间的理想平均距离。方法中，需要将引力乘以社团之间连边的权重，即：

同时，由于多层社团结构中每层中的社团半径大小不同，一个很自然的想法就是将一个社团所受到的斥力乘以另一个社团的大小。然而，这样的做法容易引起社团布局的紊乱。特别是当每层中社团半径大小差异很大时，较大的社团对较小的社团的排斥力将很大，从而将小社团排斥得很远，导致网络整体结构的不协调。因此，对于排斥力，不计社团间大小的差异，而采用原算法中排斥力的定义：

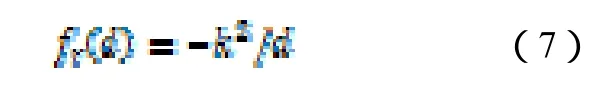
3 局部环形布局的修正

一般来说，如果两个社团间的连边越多，根据社团的定义[8]，这两个社团间的联系就越紧密，在可视化结果中的距离应该越近。但是力导引算法并不能保证连边多的社团之间拥有合适的距离，尽管在方法中社团间的连边越多它们之间的吸引力越大。所以需要在使用FR算法布局的同时，对社团的布局进行局部的修正，以弥补力导引算法本身的缺陷。为此，首先引入社团间连边密度的概念。定义多层社团结构中每层中社团A和B之间的连边密度为：

其中，表示社团A和B之间的连边数目，E表示该层中社团之间的连边总数。

引入了社团间连边密度的概念之后，就可以在使用力导引布局之前，对社团间的紧密程度先做一个总体的评估。设定一个阈值t(0t1)，当社团间的连边密度大于t时，就认为社团之间联系紧密，将这些社团取出，以便进一步的处理。在取出的所有社团中，如果社团之间有邻边，则将它们加入一个集合中，这样就可以得到一个或几个集合。对于每个集合中的社团，我们在不影响社团本身结构的情况下进行合并。合并的具体含义如下：

1.对于集合中的每个社团，保持其内部子社团的布局不变，而将集合中的所有社团视为一个新的社团，集合外任何社团对集合内部的社团的作用力将视为作用在这个新的社团上；

2.在新社团内部，集合中的所有社团进行环形布局[9]，为此，需要计算出它们的最大半径r，并通过这个最大半径计算出新社团的半径大小R，设集合中的社团个数为n，则定义R的计算公式如下：

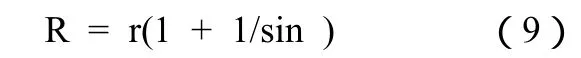
设新社团的坐标分别为 x，y,则集合中的社团（m）的坐标为：

通过以上的处理，实现了在全局使用力导引算法而局部使用环形布局的功能。实践证明，通过这种方法完全可以解决问题3，从而弥补了仅仅使用力导引算法的不足，如图6所示：

图6 环形布局示意图

5 可视化效果

按网络规模大小，从高到低依次选取3组网络数据，分别是Zachary's karate club，US Air97和Power grid，作为用于测试的网络。网络具体信息，如表1所示：

表1 用于可视化对比的网络数据信息表

使用本文提出的方法分别对以上 3个网络进行可视化布局，来考察其方法对于不同规模不同性质的网络可视化效果，如图7、图8、图9所示：

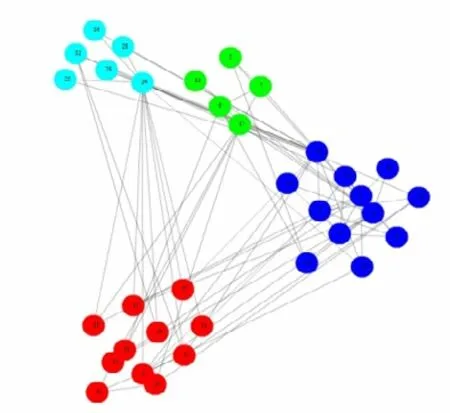
图7 对karate网络的布局效果

图8 对US air 97网络的布局效果

图9 对power grid网络的布局效果

以上3个图都取阈值等于0.3，可以看到，无论是对于大型网络，还是小型网络，我们提出的方法中社团之间的距离都较为合适，而且无论是节点还是社团分布都较为均匀，用户可以很轻松的辨认出不同的社团。由此可见，本文所提出的方法对不同规模、不同特性的网络都具有较好的布局效果，具有很好的适应性和通用性。

小结

本文提出了一种基于层次化社团结构的可视化处理方法，采用力导引算法和环形布局算法相结合的方式。这种方法既保证了联系紧密的社团之间距离合适，又能够发挥布局算法的优势，较为合理的更新节点的位置，在两种布局之间达到一种最佳平衡。同时，该方法算法复杂度并不高，从而可以更加有效地处理大规模数据。由此可见，本文所提出的方法对不同规模、不同特性的网络都具有较好的布局效果，具有很好的适应性和通用性。

[1]Battista G,Eades P,Tamassia R,Tollis I.Graph drawing:Algorithms for the visualization of graphs [M].1998,Prentice-Hall,Englewood Cliffs.

[2]Eades P.A heuristic for graph drawing [J].CongressusNumerantum,1984,42: 149-160.

[3]HadanyR,Harel D.A multi-scale algorithm for drawing graphs nicely [J].Discrete Applied Mathematics,2001,113(1):3-21.

[4]Quigley A,Eades P.FADE: graph drawing,clustering,and visualabstraction [J].Lecture Notes in Computer Science,2000,1984: 197-210.

[5]Blondel V,Guillaume J,Lambiotte R,Lefebvre E.Fast unfolding of communities in large networks [J].J.Stat.Mech.,2008,P10008.

[6]Fruchterman T,Reingold E.Graph drawing by force-directed placement [J].Software - Practice & Experience,1991,21(11): 1129–1164.

[7]Josh Barnes and Piet Hut.A hierarchical O(NlogN)force calculation algorithm [J].Nature,1986,324:446-449.

[8]Fortunato S.Community detection in graphs [J].Physics Reports,2010,486: 75-174.

[9]Breitkreutz B,Stark C,Tyers M.Osprey: A network visualization system [J].Genome Biology,2003,4(3):R22-0012.6.