基于OpenSSL库的椭圆曲线密码体制的OMNeT++实现

张求文，王景成，隆笑，赵广磊，胡霆，张震玮，何军，于长健

0 引言

近年来，随着物联网和第三代甚至第四代移动通信技术的不断发展，以及人们需求的日益增长，移动平台正以其独特的优势受到了前所未有的关注，基于移动平台的应用也层出不穷。然而，移动平台的无线环境和传感器的无人环境极大地方便了恶意攻击者，数据与隐私保护是物联网应用过程中巨大的挑战之一[1]，密钥管理机制、安全路由协议、认证与访问控制、入侵检测与容侵容错技术以及决策与安全控制等是今后研究的重点[2]。

现有的移动终端的运算能力愈发强大，比对称加密更加安全的非对称加密的运算强度已经不会成为其在移动终端上应用的瓶颈，然而，随着安全需求的增加，RSA算法所需要的密钥位数一直在增加，导致其加解密速度大为降低，存储空间显著增加，应用越来越受到限制[3]。因此人们迫切需要寻求一种运算量更小安全度更高的非对称加密算法，于是椭圆曲线密码体制孕育而生。

椭圆曲线密码体制（Elliptic Curves Cryptosystems，ECC）是近年来兴起的基于椭圆曲线离散对数问题（ECDLP）的性能优良的公钥密码体制。相比较其它的公钥加密算法，ECC有许多优点，例如由于ECDLP比DLP困难得多，椭圆曲线系统中每个密钥位的强度在本质上要比传统的离散对数系统大得多[4]，而且在计算负载、密钥大小、带宽等方面ECC均比RSA优越[5]，因此ECC非常适合计算能力和带宽传输有限却又要求高速实现加密和认证的终端场合。

对于无线终端网络的部署来说，在计算机平台上进行网络软件仿真是一个检验可行性的好办法，OMNeT++（Objective Modular Network Testbed in C++）是近年来流行在科学和工业领域的一款优秀的网络仿真平台。强大完善的图形界面接口以及编程调试等功能使得 OMNeT++迅速成长为通信网络和分布式系统的仿真主力。

1 基础算法

1.1 ECDSA

ECDSA（Elliptic Curve Digital Signature Algorithm）是一种基于椭圆曲线密码体制的数字签名算法。所谓数字签名，即是用来确认数据的来源并保护数据不被伪造的一种技术。数字签名分为签名和认证两部分，一般过程是，请求方利用自身的私钥对某特定消息进行加密处理，称为签名；认证方则利用请求方放出的公钥对签名信息进行解读，并以此验证请求方的合法性。具体算法，如表1所示[6]：

表1 ECDSA签名的生成与验证表

在表1中，参数q表示域的阶；FR为域的表示；S表示种子；a,b为椭圆曲线参数；P为基点；n为P的阶；h是余因子，具体参数如何参与运算参考文献。

1.2 ECDH

ECDH（Elliptic Curve Diffie-Hellman）是一种基于椭圆曲线密码体制的密钥交换算法，它可以使拥有各自椭圆曲线公私钥对的交换的双方在一个不安全的信道上协商出一个密钥。具体算法如表2所示[7]：

表2 ECDH密钥协商

2 接口

在 OMNeT++中，首先需要做的便是定义网络拓扑结构。在工程项目中新建一个网络描述文件（.ned文件），用simple、network、submodules、connections等关键字来定义结点、当前网络、当前网络中的节点和节点间连接方式等。随后，便是为每个定义过的节点新建.cc文件来设置节点的一系列活动。节点一般都继承OMNeT++提供的基本节点类cSimpleModule。

2.1 OMNeT++相关的常用接口

（1）、void initialize();

此函数描述了节点在初始化时候的一系列动作，例如设置节点内部自身参数等。Initialize()函数将在节点创建时被自动调用。

（2）、void handleMessage(cMessage* msg);

此函数描述了节点在接收到一条消息时的一系列动作，例如提取消息内信息和转发消息等。handleMessage()函数将在节点接收到消息时被自动调用。

为节点类定义实现以上两个函数后，节点的基本功能就算是完成了。下面给出OMNeT++中比较常用的命令接口：

（1）、Define_Module(string moduleName);

此全局命令将名字为 moduleName的节点类注册到OMNeT++中，每一个节点都必须通过将自身注册到OMNeT++中才能被识别并正确运行，所以每个节点类都必须对应一个Define_Module命令。

（2）、send(cMessage *msg,const char *gatename,int gateindex=-1);

此函数用来将消息 msg从某个门中发送出去，其中gatename为门的名字，gateindex则是名字为gatename的门的编号，所谓的门即是两个节点相连的通道。

（3）、scheduleAt(simtime_t t,cMessage *msg);

此函数用来在时间t发送一条自消息，即在时间t向节点自身发送消息 msg，一般被用来定时地主动触发节点的handleMessage()函数。其中时间t可以用simTime()函数来返回当前仿真时间，而节点在handleMessage()函数中可以使用msg-＞isSelfMessage()函数来判断收到的消息是否为自消息。

一些情况下，OMNeT++自带的cMessage消息不能满足项目的需求，此时可以通过新建.msg文件并通过 message关键字来创建自定义的消息类，在其中可以为自定义消息类添加各种变量，以满足项目的需求。当然，在创建了.msg文件后还需在OMNeT++的命令行窗口使用opp_msgc命令来创建.msg对应的.cc和.h文件，并在需要使用的地方将.h文件包含进来，便可以正常使用。

为了在OMNeT++中实现ECDSA等算法，还需要一个密码学领域的函数库，而OpenSSL便是一个很好的选择。OpenSSL囊括了主要的密码学算法、常用的密钥和证书封装管理功能以及 SSL协议，同时以 C语言为开发语言的OpenSSL也提供了优秀的跨平台性能。

2.2 OpenSSL中与ECDSA算法相关的接口

（1）、EC_KEY EC_KEY_new_by_curve_name(int nid);此函数根据参数 nid来返回一条内置的 SEC（Standard for Efficient Cryptography）推荐的椭圆曲线，OpenSSL提供了类似 NID_secp192k1的宏来方便使用者选择安全的椭圆曲线。

（2）、int EC_KEY_generate_key(EC_KEY* key);此函数将会在椭圆曲线对象key内部随机生成私钥和公钥。

（3）、int ECDSA_sign(int type,const unsigned char* dgst,int dgstlen,unsigned char* sig,unsigned int* siglen,EC_KEY*eckey);此函数用来对在椭圆曲线对象eckey上长度为dgstlen的字符串dgst进行数字签名，并存放在字符串sig中。

（4）、int ECDSA_verify(int type,const unsigned char*dgst,int dgstlen,const unsigned char* sig,int siglen,EC_KEY* eckey);此函数用来对在椭圆曲线对象eckey上长度为siglen的字符串sig进行数字签名认证，解签名的结果放入字符串dgst中，并返回认证成功与否。

2.3 OpenSSL中与ECDH算法相关的接口

（ 1）、 int EC_POINT_set_affine_coordinates_GFp(const EC_GROUP* group,EC_POINT* p,const BIGNUM* x,const BIGNUM* y,BN_CTX* ctx);

此函数用来设定椭圆曲线group的G点坐标。

（ 2）、 int EC_POINT_add(const EC_GROUP* group,EC_POINT* r,const EC_POINT* a,const EC_POINT* b,BN_CTX* ctx);

此函数用来完成对椭圆曲线group上的点加计算，计算结果放入点r，其中。

（ 3）、 int EC_POINT_mul(const EC_GROUP* group,EC_POINT* r,const BIGNUM* n,const EC_POINT* q,const BIGNUM* m,BN_CTX* ctx);

此函数用来完成对椭圆曲线group上的点乘计算，计算结果放入点r，其中r=G×n+q×m ，G为椭圆曲线group的基点。

3 实现及对结果的分析

3.1 在OMNeT++中实现ECDSA的核心代码

3.2 在OMNeT++中实现ECDH的核心代码

3.3 实验结果及分析

本文测试所使用的机器具体配置是CPU为Intel Core i3 380M，主频为2.53GHz。算法耗时性能指标，如表3所示：

表3 耗时性能指标

算法耗时曲线图，如图1所示：

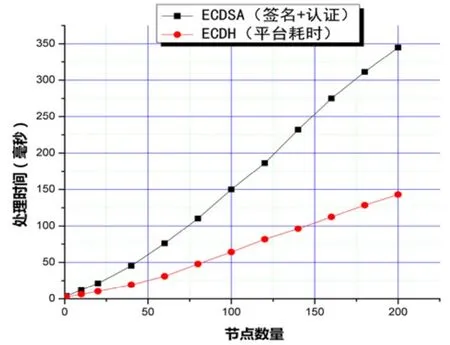
图1 平台处理时间与节点数量关系图

从上面的表格数据以及曲线图中可以看到，就ECDSA签名算法来说，节点在100以后基本呈线性增长趋势，而在100个节点以下的时候，平台处理时间与节点数呈非线性关系，故而在整体网络节点超过100的时候，具体平台处理时间等即为可估计参数。

相比于 ECDSA一次签名认证成功后即不再进行，ECDH在每次密钥更新后都要重新进行，故而ECDH的时间与节点关系更值得考虑，但是从图1可以看出，红色曲线基本上呈线性增长趋势，在节点数量少于100时的非线性特征也较为不明显，故而可以较好的估计平台整体时间消耗。

最后，由图1中的数据可以看出，节点数量纵使达到200后，平台的处理时间仍旧不到0.4s，而密钥交换所用时间更是不到 0.15s。而文章仿真所用电脑的性能更是远远低于工程应用的服务器设备，故而椭圆曲线密码体制在工程项目中的具体应用具有十分良好的发展前景。

4 总结

本文介绍了包括ECDSA和ECDH协议的椭圆曲线密码体系的具体算法及实现方法，并详细描述了基于OPENSLL库的 OMNET++的各方面基本接口和库函数相关接口及其应用方法。介绍了ECDSA和ECDH实现的核心代码内容，并仿真验证了可行性。最后，通过平台时间消耗和节点数量的关系图，对椭圆曲线密码体制的可应用性进行了说明。

[1]ITU.The Internet of Thing [EB/OL].(2005-12-17)[2010-07-03].http://www.itu.int/internetofthings

[2]杨庚，许建，陈伟，祁正华，王海勇.物联网安全特征与关键技术[J].南京邮电大学科技处；南京邮电大学计算机学院，2010(04)

[3]徐学洲，何云升.椭圆曲线密码体制应用研究.[M]西安电子科技大学出版社，2006

[4]Don B Johnson,Alfred J Menezes.Elliptic Curve Digital Signature Algorithm (ECDSA)[Z/OL].http://www.certicom.com/resources/download/ecdsa.ps.

[5]王德力.ECDSA在移动电子商务中的应用.[M]东北大学出版社，2005

[6]张伟.ECDSA算法实现及其安全性分析[J].信息与电子工程，2003(02)

[7]邵晓博.椭圆曲线密码体制中密钥协商方案改进的研究[J].计算机安全，2010(02)