半导体温控系统的自抗扰控制器设计

廖晓文 陈政石 田志波 黄瑞龙

(广东石油化工学院自动化系，广东 茂名 525000)

半导体温控系统的自抗扰控制器设计

廖晓文 陈政石 田志波 黄瑞龙

(广东石油化工学院自动化系，广东 茂名 525000)

针对半导体温控系统大时间常数、时滞较大且易受参数扰动影响的问题，提出了自抗扰控制(ADRC)技术。针对自抗扰控制器待调节参数多、参数整定较为困难的问题，从fal函数特性及扩展状态观测器(ESO)设计出发，确定了自抗扰控制器的参数，并探讨了如何准确估计建模误差与外扰。仿真试验表明，系统在半导体致冷器件优值系数、冷热端温差发生变化及受到电压纹波干扰时均具有良好的鲁棒性能和动态性能。

半导体温控系统 自抗扰 参数扰动 参数设置 ESO

0 引言

半导体致冷器的操作具有可逆性，可同时用于加热或制冷，具有效率高、耗电量低，能直接将电能转化为热能等优点，可应用在一些空间受到限制、可靠性要求高的场合。然而，使用半导体致冷器构建的温控系统受输入电流、优值系数、环境温度等因素影响而变化的规律十分复杂［1］，是高度非线性系统。此外，温控系统属于大时间常数且时滞较大的控制系统，采用常规的PID控制，往往会出现超调大、调节时间长、抗干扰能力和鲁棒性变差等问题［2］。

自抗扰控制器(active disturbance rejection controller，ADRC)是用扩张状态观测器(extended state observer，ESO)和非线性状态误差反馈控制率(nonlinear state error feedback law，NLSEF)构造的新型控制器。自抗扰控制器能以一套不变的参数，对存在外干扰、状态时滞、输入时滞的不确定性系统具有理想的控制效果［3］。同时，还可以通过采用跟踪微分器(tracking differentiator，TD)安排过渡过程，解决快速性与超调的矛盾。然而，独立于对象模型的自抗扰控制器有较多待调节参数，存在参数难调的问题。虽然研究者提出了基于时间尺度［4］、遗传算法［5］、控制器带宽［6］等参数整定方法，但这些比较复杂的方法大多并没有关注fal函数特性和ESO的具体设计。

本文结合半导体温控系统的数学模型，从fal函数特性、ESO设计出发，设计了自抗扰控制器，并给出了仿真及试验结果。

1 温控系统的数学模型

半导体温控系统由两块半导体致冷片TEC12706、散热片、冷块及隔热层构成。由于空气的热传导速度较慢，因此，温控系统可用一阶纯滞后过程来进行描述［7］。

根据该系统的阶跃响应，利用Matlab系统辨识工具箱的Process模块，可辨识得到温控系统的传递函数，如式(1)所示:

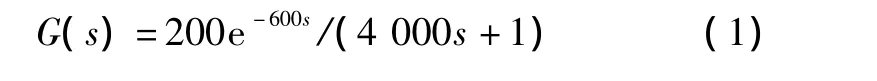
2 自抗扰控制器设计

2.1 自抗扰控制器

以一阶对象为例，一阶对象的方程为:

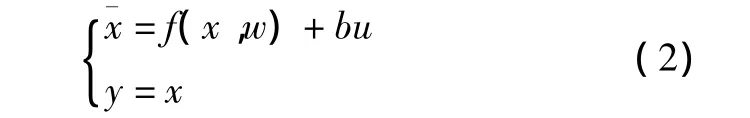
式中:x为对象状态变量;u为输入;y为输出;f(x，w)为模型未知部分。对应的一阶自抗扰控制器为:

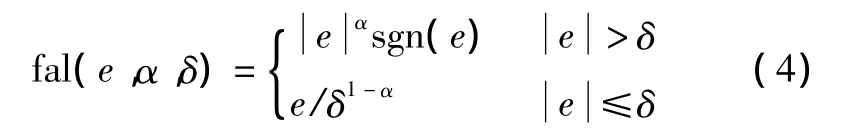
式中:α为反馈幂次(当0＜α＜1时为非光滑反馈);δ为用于区别偏差e大小的界限。单纯从抑制扰动能力看，高次幂的反馈不如低次幂的反馈;而从抑制扰动的效率看，增大反馈增益k不如减小幂次α。反馈增益k的增大只能以反比例的方式减小稳态误差，但幂次α能以数量级的方式减小稳态误差［9］。

2.2 扩张状态观测器(ESO)

根据温控系统的数学模型，温控系统加热、制冷的温度响应特性可由一阶惯性环节200/(4 000 s+1)和纯延时环节1/(600 s+1)来近似描述。结合电路增益G为1/50，可以严格依照传递函数建立ESO。

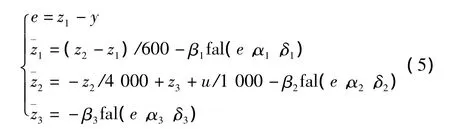
式中:y为系统的输出温度;z1为ESO对y的观测值;z2为传递函数200/(4 000 s+1)的输出，也是传递函数1/(600 s+1)的输入;z3为建模误差与外界扰动的观测值总和。虽然该ESO物理、数学意义明显，但是z2不容易通过测量对应物理量来验证观测结果，且ESO关于z1、z2项表达过于复杂，参数难以调节。

结合电路增益G，整理传递函数200/(4 000s+1)、1/(600s+1)，可得到 1/［1 000(600s2+1.15s+1/4 000)］。据此建立微分方程并进行化简，得到600++y/4 000=u/1 000，设计的ESO如下。

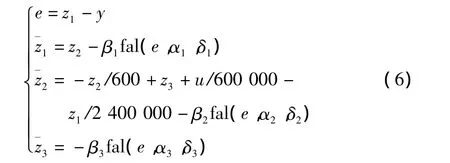
式中:y仍为系统的输出温度;z1为ESO对y的观测值，z2为z1的微分。控制器输出u为电流值，其输出范围在-12～15 A之间。

此外，结合温度控制系统的实际温度，还可以消去(u/600 000-z1/2 400 000)。虽然简化传递函数改变了系统的时间常数与时滞系数，但可将此归为建模误差，可通过z3进行观测与补偿。相对于上一个ESO，该ESO结构简单，计算复杂度较低，同时具有参数易调的优点。由于y是一个可测量，y的微分可以通过y及采样周期间接获取，因此，可通过测量对应的物理量来校正观测结果，从而保证 z1、z2估计准确。根据式(6)，若z1、z2估计准确，则容易保证z3估计准确，从而能准确估计出建模误差与扰动。

2.3 跟踪微分器(TD)

在应用中，通过结合TD安排过渡过程来解决快速性与超调之间的矛盾。TD可以用式(7)来表示。

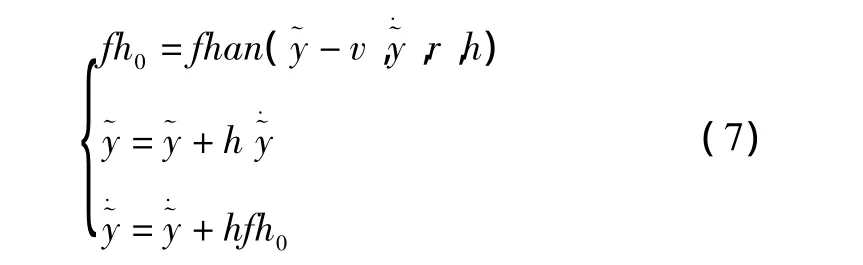
式中:v为设定值;r为速度，由过渡过程时间T0决定;h 为步长。fhan 函数如式(8)所示，其中，d、d0、val、a0均为过渡变量。

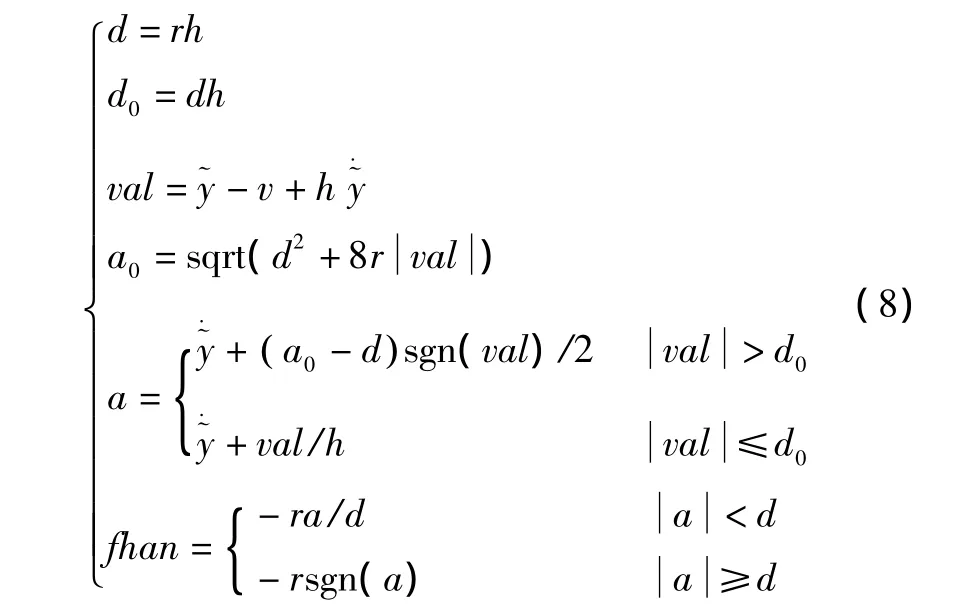
2.4 系统控制架构

结合非线性状态误差反馈控制率与跟踪微分器安排过渡过程，系统的控制架构如图1所示。图1中，u的单位为安培，G为电路增益，其值为1/50。

图1 系统控制架构Fig.1 System control structure

控制器的输出为:

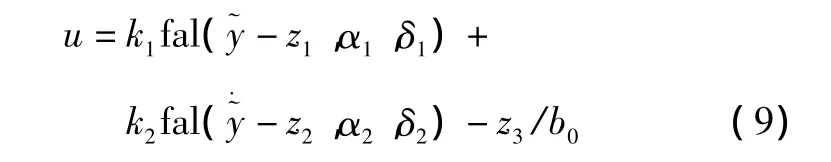
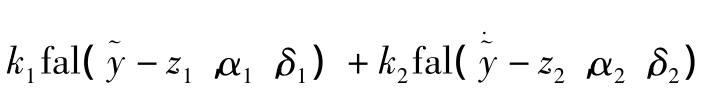
3 仿真与试验结果

自抗扰控制器(ADRC)的各个模块可以单独调节参数。对于TD，取步长h=5、r=0.000 8，设定过渡过程时间为5 000 s。在ESO参数设置方面，根据fal函数特性，减小幂次系数α能增加扰动抑制效率，因而可设置α1=0.75、α2=0.5、α3=0.25。由于已采用 TD 安排过渡过程来解决系统快速性与超调的矛盾，因此参照式(4)，可设置 δ1=δ2= δ3= δ=1。对式(6)进行拉普拉斯变换，整理得:

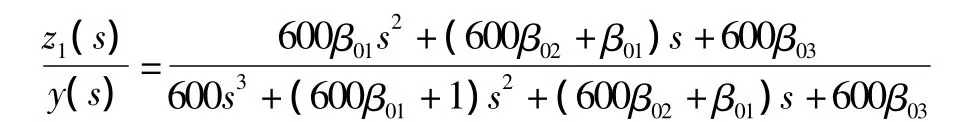
式中:β01= β1/Δ;β02= β2/Δ;β03= β3/Δ。由于使用了TD安排过渡过程，可取 Δ=δ1-α，因而有 Δ=1。当600β01＞＞1时，系统对阶跃输入、斜坡输入和加速度输入均无稳态误差［10］。

根据扰动抑制要求和 fal函数特性，取 β1、β2、β3的搜索范围为 0.3≤β1≤3、0.01≤β2≤0.5、0.01≤ β3≤0.1，可搜索得到 ESO 的增益为 β1=2、β2=1/10、β3=1/20。在实际应用过程中，可在此基础上根据实际观测结果微调增益系数。同理，根据fal函数特性及系统估计误差，NLSEF 的参数设置为:δ1=0.1、δ2=0.01、k1=220、k2=1 000、α1=0.75、α2=0.5。ESO 的估计误差如图2 所示，其中，e1=z1-y≤0.01，e2=z2-y.≤0.03。

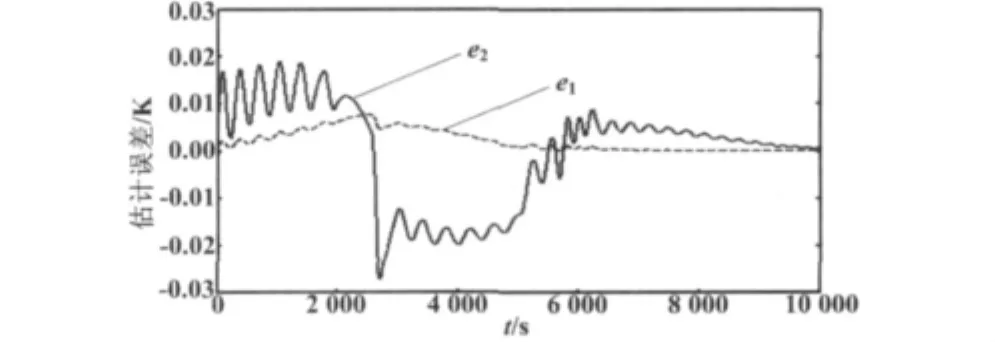
图2 ESO的估计误差Fig.2 Estimation errors of ESO

将传递函数改为180/(4 200 s+1)，模拟优值系数和冷热端温度变化，并在传递函数180/(4 200 s+1)前加上幅度为1、频率为3.14 rad/s的正弦波，模拟电压纹波干扰。

系统输出曲线如图3所示。

图3 系统输出曲线Fig.3 System output curves

由图3可知，受干扰时的输出曲线在5 000 s时精度达到-0.4 K，7 000 s时达到最大超调0.3 K，稳态误差小于0.01 K，与未受干扰时的输出曲线类似。建模误差补偿曲线及合成误差的补偿曲线如图4所示。

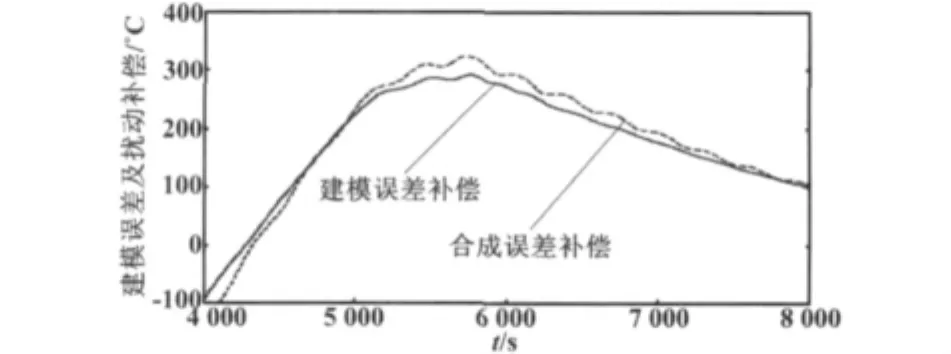
图4 建模误差补偿及合成误差补偿曲线Fig.4 Curves of modeling error compensation and synthesis error compensation

温度传感器选用 MF51-103NTC热敏电阻，在-10～50℃期间热敏电阻的阻值在44～4 kΩ之间。选择三个定值为24 kΩ的高精度金属膜电阻组成单臂电桥，电桥采用恒流源供电，供电电流5 mA。经二级运放，将输出电压放大至0.3～2.7 V，经过软件非线性校正，可在-10～50℃范围内达到0.05 K的检测精度。利用温控系统将温度控制在20℃，然后设定温度控制的目标值为40℃，单片机STC12C5608每隔5 s将采样到的温度数据发送至上位机。根据串口数据得到的升温曲线如图5所示。

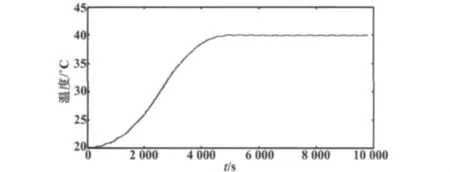
图5 串口温度数据图Fig.5 Serial port temperature data

4 结束语

本文从fal函数特性出发，确定fal函数的相关参数，通过简化的模型设计ESO，由ESO估计外部扰动与建模误差，并结合NLSEF完成前馈补偿。仿真及试验结果验证了此方法的可行性，本方法能有效降低自抗扰控制器的设计难度，对推广自抗扰控制器的应用具有一定的参考价值。

［1］毛佳妮，申丽梅.半导体制冷器制冷性能的综合影响因素探讨及其优化设计分析［J］.流体机械，2010，38(7):68-73.

［2］曾河华，李东海，姜学智.时滞对象的自抗扰PID控制［J］.清华大学学报:自然科学版，2007，47(11):2017-2021.

［3］夏元清，黄焕袍，韩京清.不确定时滞系统ADRC控制［J］.中南工业大学学报:自然科学版，2003，34(1):383-385.

［4］邵立伟，廖晓钟.基于时间尺度的感应电机自抗扰控制器的参数整定［J］.控制理论与应用，2008，25(2):201-205.

［5］刘丁，刘晓丽，杨延西.基于遗传优化自抗扰控制器的机器人无标定手眼协调［J］.机器人，2006，28(5):510-514.

［6］ Gao Zhiqiang.Active disturbance rejection control:a paradigm shift in feedback control system design［C］∥Proceedings of the 2006 American Control Conference Minneapolis，Minnesota，USA，June 14-16，2006:2400-2407.

［7］王茂，曾庆双，刘赤，等.测试转台温控箱的计算机控制［J］.中国惯性技术学报，1998，6(4):89-93.

［8］王宇航，姚郁，马克茂.Fal函数滤波器的分析及应用［J］.电机与控制学报，2010，14(11):88-92.

［9］韩京清.自抗扰控制技术［M］.北京:国防工业出版社，2008:123-125.

［10］Ogata K.现代控制工程［M］.4版.北京:电子工业出版社，2003:660-661.

Design of Active Disturbance Rejection Controller for Semiconductor Temperature Control System

Active disturbance rejection control(ADRC)technique is adopted to solve the problems in semiconductor temperature control systems，e.g.，large time constant，large time delay and sensitive to parameter disturbances.In accordance with the features of active disturbance rejection controller，including multiple parameters must to be adjusted，and difficult for tuning parameters，based on characteristics of fal function and the design of extended state observer(ESO)，the parameters of ADRC are determined，and the methods to accurately estimate modeling error and external disturbance are discussed.Simulation tests show that the system offers strong robustness and good dynamic performance when merit coefficient and temperature difference between hot and cold ends of semiconductor refrigeration devices change，or interfered by voltage ripples.

Semiconductor temperature control system Active disturbance rejection Parameter disturbance Parameters setting ESO

TP273

A

茂名市科技计划基金资助项目(编号:20101023)。

修改稿收到日期:2011-10-04。

廖晓文(1977-)，男，2005年毕业于广东工业大学机械电子工程专业，获硕士学位，讲师;主要从事工业控制仪表、运动控制技术方面的研究及设计工作。

行业信息