杉树坳隧道台阶法开挖初期支护变形规律分析
马显红
(贵州高速公路开发总公司,贵州 贵阳 550004)
杉树坳隧道台阶法开挖初期支护变形规律分析
马显红
(贵州高速公路开发总公司,贵州 贵阳 550004)
以杉树坳隧道工程为背景,分析了台阶法施工的拱顶下沉规律,主要是台阶法衬砌变形与开挖施工进度的关系,探究应力释放过程,对监测数据进行分析得出,上台阶开挖导致拱顶沉降量达到总沉降量的70%以上,进而得到施工过程中的应力释放系数。将此应力释放系数应用于有限元模型计算,把数值计算成果与拱顶下沉实测值进行了比较,证明了该模型能够较为准确地反映上下台阶开挖对初期支护变形的影响,从而为台阶法开挖的数值模拟以及施工过程的控制提供依据。
台阶法 初期支护 变形规律 应力释放系数 有限元法
台阶法施工由于多步开挖、多次爆破,反复发生应力再分配对围岩造成扰动破坏,隧道周边变形伴随每步开挖都出现较显著的增长[1]。为实现对施工过程的控制,研究台阶法施工围岩的变形规律影响至关重要。拱顶下沉由于其量测方法简单可靠,可明显反馈围岩和初期支护的变形和稳定情况,且受施工步骤影响较大,可对隧道围岩变形的稳定性进行及时评价,为二次衬砌提供合理的施作时机,并可对变形较大的围岩段及时预测预警,因此,拱顶下沉成为隧道变形稳定性评价的关键指标。
关宝树、施成华、刘宝琛等[2-6]分别总结了浅埋暗挖法施工中沿隧道轴线纵向的下沉动态规律;张顶立等[7]通过对深圳地铁一期工程部分区间隧道拱顶下沉的回归分析,并通过数值模拟验证,认为隧道拱顶下沉过程遵循指数函数的关系;姜德义等[8]基于遗传算法的神经网络建立了隧道拱顶下沉的时序预测模型。这些研究在隧道施工中拱顶下沉规律及预测方面取得了一定成果,但都没有涉及将拱顶下沉与台阶法施工相联系,从而探究台阶法施工对拱顶下沉量的影响。
本文根据杉树坳隧道拱顶下沉与上下台阶之间的相互关系探究应力释放过程,得到相应施工过程中的应力释放规律,作为台阶法开挖施工过程的依据。
1 工程背景
杉树坳隧道位于厦蓉高速公路(贵州境)水口至榕江格龙段,为分离式长隧道,左线长2 445 m,最大埋深232 m;右线长2 412 m,最大埋深225 m。隧道区处于贵州高原东南缘,地势西高东低,属构造侵蚀型中低山沟谷地貌。隧道轴线穿越地层为南沱组一段,岩性为薄~中厚层变余砂岩,局部夹含砾板岩。地下水主要沿基岩面及风化岩体内裂隙及结构面向低洼处渗流,雨季水量较大。
隧道采用新奥法原理设计,根据地质条件采取了上下台阶法进行开挖,初期支护采用了锚喷支护。
本文选取两个典型断面YK42+681、YK40+379,分别位于杉树坳隧道右线进口、出口段,围岩为灰色强风化变余砂岩,整体较破碎,节理裂隙发育,呈碎裂块状结构,稳定性差,YK42+681围岩级别为Ⅴ级,YK40+379为Ⅵ级。
2 拱顶下沉监测布置情况
拱顶下沉是隧道拱顶内壁的绝对下沉量。拱顶是隧道周边的一个特殊部位,扰度最大,拱顶的下沉情况具有较强的代表性和显示作用。拱顶下沉量主要是监视拱顶下沉,了解断面的变形情况,判断拱顶的稳定性,防止塌方等风险事故的发生。本隧道拱顶下沉监测实施情况如下。
每个量测断面的拱顶中心用小型钻机钻5 cm左右深的小孔,然后把孔径相同的膨胀螺丝钩塞到孔中,用扳手将膨胀螺钩拧紧,作为前视点挂钩(G1,G2,G3),见图1。同法在距测点30 m以外的相对稳定的初期支护上布置一后视测点挂钩。在下一次爆破循环前获得初始读数,初读数在开挖后12 h内读取,最晚不超过24 h,而且在下一循环开挖前,完成初期变形值读数。
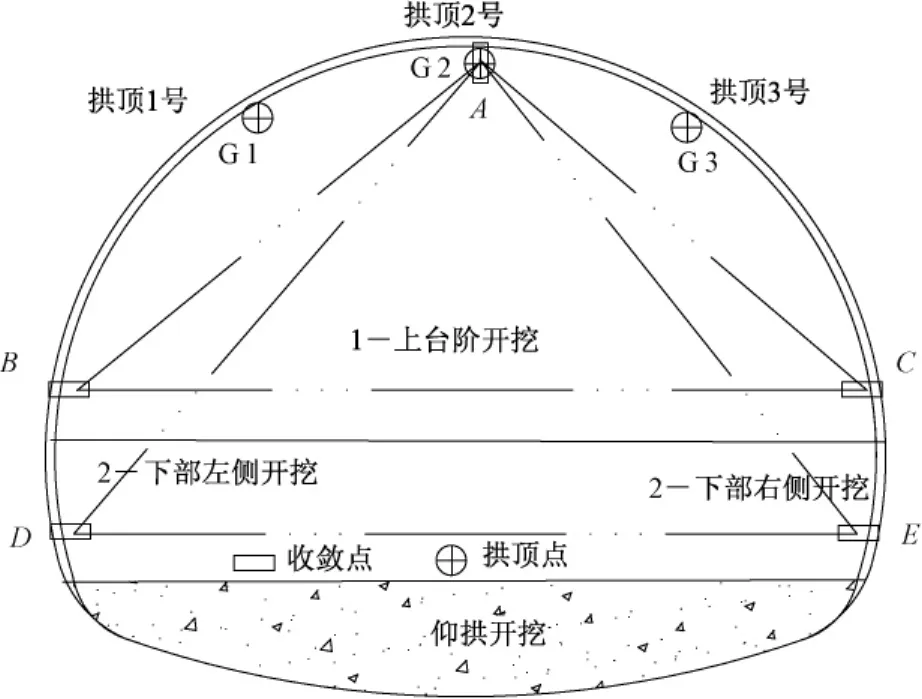
图1 洞内断面测点布置(拱顶下沉测点:G1,G2,G3)
在量测断面的拱顶中心及隧道两侧距中心0.5 m范围各设一个测点,先用小型钻机在待测部位成孔,用全站仪进行量测,在挂钩上安装反光贴片,后视点设置在相对稳定的二次衬砌断面上。
量测频率按《公路隧道施工规范》执行[9],如表1所示。

表1 隧道拱顶下沉监测频率
3 拱顶下沉量测数据分析
3.1 YK42+681监测断面
上台阶掌子面开挖过4 m后布置拱顶下沉监测断面YK42+681,此时下台阶掌子面距离监测断面36 m。施工过程中,上下台阶掌子面保持30~40 m的距离,施工时间差约为30 d。拱顶下沉测点沉降值随时间变化曲线如图2所示。

图2 Y K42+681初期衬砌拱顶沉降量随时间变化曲线
由图2可见,上台阶开挖后,受施工爆破扰动影响,拱顶各个测点下沉明显,随着掌子面的继续推进和时间的推移,监测10 d后下沉速度减小,变形渐趋平稳。中间测点G2沉降量于上台阶掌子面距离超过监测断面3D时开始处于稳定值,为10~11 mm,这一过程中的变形占总变形量的74.5%。当下台阶掌子面开挖至距离监测断面10 m远时,施工爆破造成监测断面处的围岩又一次的扰动和应力重分布,拱顶下沉再次出现较大增长。中间测点G2沉降值于下台阶掌子面超过监测断面5D处时达到最大值,为18 mm,下台阶开挖一周后,随着下台阶掌子面的远离,拱顶下沉变化速率逐渐减缓,下沉量达到稳定状态并略有回升趋势。这一过程中的变形占总变形量的25.5%。
拱顶下沉监测断面YK42+681三个测点随上下台阶开挖的最大沉降值统计如表2所示。

表2 YK42+681拱顶下沉测点随上下台阶开挖的最大沉降值
3.2 YK40+379监测断面
上台阶掌子面开挖过2 m后布置拱顶下沉监测断面YK40+379,此时下台阶掌子面距离监测断面19 m。施工过程中,上下台阶掌子面保持约20 m的距离。拱顶下沉测点沉降值随时间变化曲线如图3所示。
由图3可见,上台阶开挖时,受施工爆破扰动影响,拱顶下沉明显,随着掌子面的远离和时间的推移,变形速率逐渐减小,拱顶下沉经历15 d的持续下降后,变形量渐趋平稳。测点 G1,G2,G3沉降量于上台阶掌子面距离超过监测断面2D时开始处于稳定值,中间测点G2沉降值达37.7 mm,这一过程中的变形占总变形量的73.5%。下台阶开挖时,施工爆破造成围岩二次扰动,应力重分布,拱顶下沉测点沉降值又一次显著下降并随着下台阶掌子面的远离再次趋于稳定,中间测点G2沉降值最终沉降量为51.3 mm,这一过程中的变形占总变形量的26.5%。
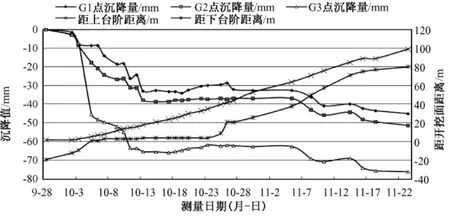
图3 Y K40+379初期衬砌拱顶沉降量随时间变化曲线
拱顶下沉监测断面YK40+379三个测点随上下台阶开挖的最大沉降值统计如表3所示。
综合以上两个监测断面拱顶下沉情况,可得如下规律:
怒江州政府从2003年开始大量招商引资,推进中小水电开发。国家发改委评审通过了《怒江中下游水电规划报告》,计划了在怒江修建“两库十三级”电站的开发方案,但上述规划方案遭到了环保组织的反对。在随后的十一五、十二五国家能源发展规划中,怒江水电开发的计划一直位列其中。通过民间环保力量的不懈努力,经过十多年保护与开发的探讨,在2016年12月的能源发展十三五规划中,怒江水电开发终于出列。
1)上下台阶开挖至监测断面前后,拱顶的三个测点沉降量均出现一定程度的突变,拱顶下沉经历了三个阶段:急剧变形阶段、缓和变形阶段及基本稳定阶段。
2)上台阶开挖后10~15 d内,围岩变形很强烈,拱顶下沉量达到总下沉量的70%。强烈变形过后,由于岩土体材料的黏弹性,围岩变形进入波动期并很快进入缓慢变形期,变形趋于平衡。
3)下台阶开挖时,对上部围岩扰动较小,下台阶开挖导致的拱顶下沉量只占总下沉量的30%。

表3 YK40+379拱顶下沉测点随上下台阶开挖的最大沉降值
4 数值模拟分析
4.1 有限元模型的建立
本次数值模拟作为平面问题处理,物理模型定为弹性模型。为消除边界效应,所建立的模型具有足够大的尺寸,模型范围为隧道长宽的3倍以上。因监测数据均量测于二次衬砌施作前,故数值模拟中只考虑初期支护作用,C20喷射混凝土等效为梁单元,φ25中空锚杆等效为杆单元。根据实际经验与隧道开挖理论,模型两侧边界设为水平位移约束,下边界设为竖直位移约束,上边界为自由边界。
在上下台阶施工模拟时,围岩应力分步释放。根据监测数据统计,得到上台阶支护完成后应力释放75%,下台阶支护完成后应力释放25%。计算分5个增量步:①初始地应力计算;②上台阶开挖;③上台阶初期支护;④下台阶开挖;⑤下台阶初期支护。
计算中围岩重度参考勘察报告,支护结构物理力学参数来自隧道设计资料,其它计算参数按照公路隧道设计规范[10]取值,如表4和表5所示。
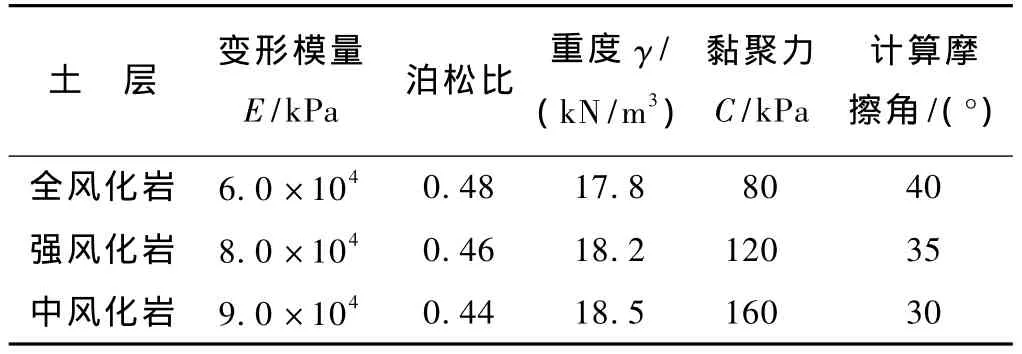
表4 YK40+379处Ⅵ级围岩计算参数
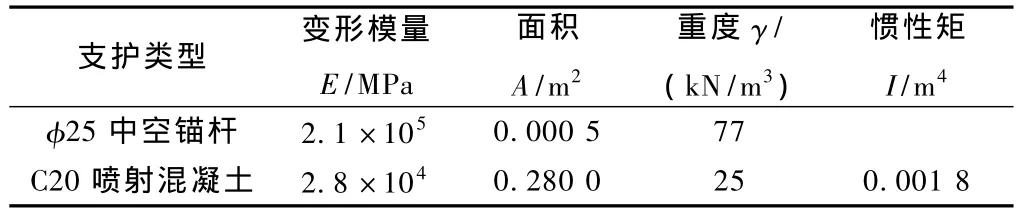
表5 支护结构物理力学参数表
4.2 有限元计算结果

图4 计算断面变形云图(上台阶开挖)(单位:m)
4.3 计算结果分析
计算断面的拱顶下沉计算结果与实测值对比见表6。从实测结果来看,隧道的拱顶最终下沉量为51.3 mm,而数值模拟的拱顶最大下沉量为48.9 mm;上台阶开挖支护完毕时,隧道拱顶实测下沉量为37.7 mm,而数值模拟的下沉量为37.4 mm。计算结果和实测结果基本相符合。

图5 计算断面变形矢量图(上台阶开挖)(单位:m)

图6 计算断面变形云图(开挖完成后)(单位:m)
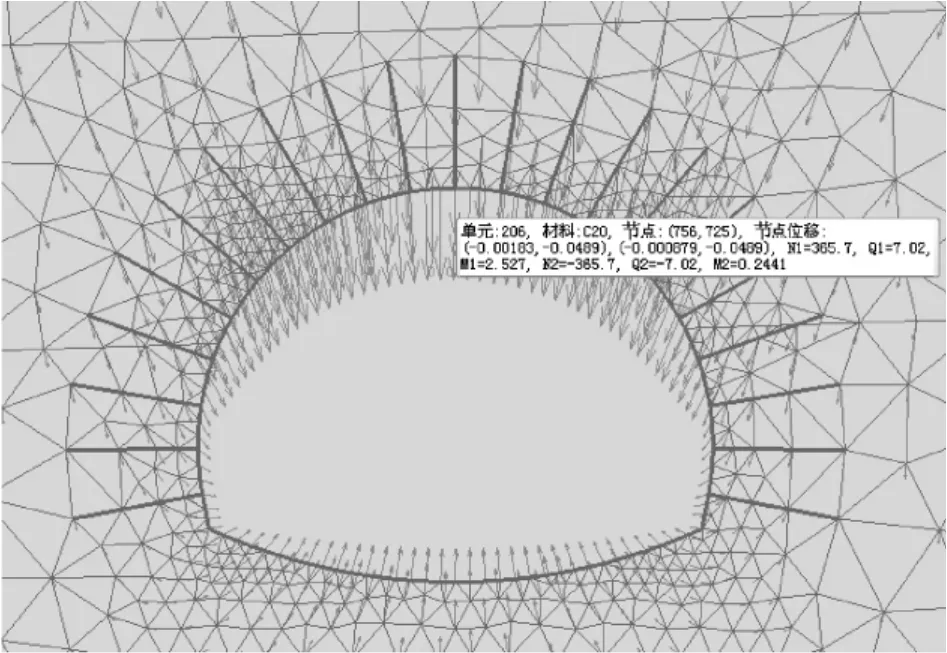
图7 计算断面变形矢量图(开挖完成后)(单位:m)
从数值模拟和实测数据对比可知,本次数值模拟计算效果较好,可在指导施工实践中起到一定的参考作用。由计算结果与实测值可知,上台阶开挖拱顶沉降量占总沉降量的绝大部分,因此在上台阶施工中应注意开挖进尺和爆破装药量等,尽量减弱施工扰动的影响。
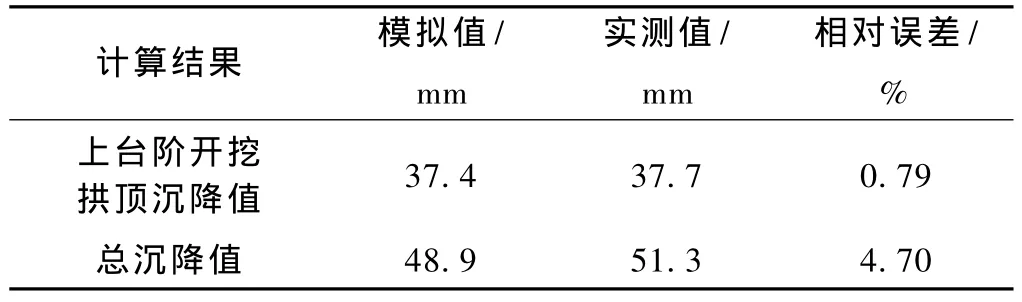
表6 计算结果与实测值的对比
5 结论
本文通过对杉树坳隧道台阶法施工的现场实时监测数据分析与数值模拟对比,研究了台阶法开挖施工进度与变形之间的关系,得到如下主要结论:
1)隧道上下台阶开挖前后拱顶下沉都经历了三个阶段:急剧变形阶段、缓和变形阶段及基本稳定阶段。上台阶开挖引起的拱顶变形是总变形的主要组成部分,可达到总变形量的70%以上。
2)隧道下台阶开挖及初期支护30 d左右,围岩基本稳定,可按规范要求适时施作二次衬砌。
3)通过现场监控量测,可及时掌握围岩和初期支护在施工中的变形情况及稳定程度,为评价和修改初期支护参数、保证隧道施工安全和二次衬砌施作时间提供依据。
4)通过典型断面的数值模拟,对隧道拱顶下沉随施工工序变化的实测值与计算值进行对比,通过监测数据确定应力释放系数规律,进一步通过数值模拟分析,预测围岩变形是可行的。
[1]李晓红.隧道新奥法及其量测技术[M].北京:科学出版社,2002.
[2]关宝树,国兆林.隧道及地下工程[M].成都:西南交通大学出版社,2002.
[3]苏兴.监控量测技术在浅埋大跨度双线铁路隧道中的应用[J].铁道建筑,2011(7):60-62.
[4]施成华,彭立敏,刘宝琛.浅埋隧道施工引起的纵向地层移动与变形[J].中国铁道科学,2003,24(4):87-91.
[5]施成华,彭立敏.浅埋隧道开挖纵向地表变形预测及其基本规律[J].中国公路学报,2004,17(2):73-77.
[6]阳军生,刘宝琛.城市隧道施工引起的地表移动及变形[M].北京:中国铁道出版社,2002.
[7]张顶立,黄俊.地铁隧道施工拱顶下沉值的分析与预测[J].岩石力学与工程学报,2005,24(10):1703-1707.
[8]姜德义,任松,刘新荣,等.隧道拱顶下沉时序遗传算法神经网络预测模型[J].地下空间与工程学报,2006,2(4):547-550.
[9]中华人民共和国交通部.JTG F60—2009 公路隧道施工技术规范[S].北京:人民交通出版社,2004.
[10]中华人民共和国交通部.JTG D70—2004 公路隧道设计规范[S].北京:人民交通出版社,2004.
U455.4
A
1003-1995(2012)01-0044-04
2011-04-19;
2011-10-18
马显红(1971— ),男,贵州贵阳人,高级工程师。
(责任审编 白敏华)

