第42届国际物理奥林匹克竞赛实验试题简介

荀 坤，张朝晖，刘树新，陈晓林

（北京大学物理学院，北京100871）

1 引 言

第42届国际物理奥林匹克竞赛于2011年7月10日至7月18日在泰国首都曼谷市举行，代表中国参赛的5名中学生全部都获得了金牌，其中李蓝青同学获总分第5名和理论满分.

本届竞赛的2道实验题都是黑盒子型，分别是“电学黑盒子——电容式位移传感器”和“力学黑盒子——1个内含小球的圆筒”.我们将尽可能展现试题原貌，利用标准数据给出解答.

2 试 题

2.1 试题1：电学黑盒子——电容式位移传感器

振荡频率为f的弛张振荡器含有1个电容为C的电容器，f与C的关系如下

其中：a是常量，CS是电路的杂散电容，频率f可用数字频率计测量.

待测电学黑盒子是平板电容器.它由上下2个极板构成，下极板固定不动，上极板可沿1个方向滑动.2个极板之间有介电材料隔开.每个极板都是梳状结构，每个梳齿的形状都相同.滑动上极板就可以改变黑盒子的电容值.

实验装置如图1所示，1个弛张振荡器，1个含频率计的数字万用表，1套已知电容值的电容，1个电学黑盒子（平板电容器）和1节电池，其中定标用电容器的标称电容值参见表1.

图1 试题1的实验装置图

表1 定标用电容器的标称电容值

2.1.1 定标（3.0分）

采用不同已知电容值的电容器，测量振荡电路的振荡频率f.通过恰当作图，求出a和CS的数值.不要求做误差分析.

2.1.2 确定平板电容器的几何形状（6.0分）

黑盒子内电容极板有3种可能的几何形状，如图2所示.

针对每种可能的几何形状，定性绘出电容C随上极板位置变化的预期曲线.然后，测量f与上极板位置的关系，绘出相应的曲线，并由此推出平板电容器的平板形状和尺寸（即求出b和w的值）.已知上、下极板之间的距离d＝0.20mm.两极板之间介质层的相对电容率为εr＝1.5.真空电容率为ε0＝8.85×10－12F·m－1.不要求做误差分析.

图2 平板电容器电极可能的几何形状的俯视图

2.1.3 数字卡尺的分辨率（1.0分）

2个极板之间的相对位置变化时，电容器的电容值随之变化.依此原理可以制造数字卡尺.如果本实验中的平行板电容器被用作数字卡尺，请由第2部分的实验数据估计该卡尺的分辨率：即对f≈5kHz，求出可以分辨的最小距离.对最终的结果不需要做误差估计.

2.2 试题2：力学黑盒子——1个内含小球的圆筒

1个圆筒，质量为M，在与其一端距离z处固定有一质量为m的小球.垂直其中轴线钻有一系列用于支承圆筒在竖直平面内摆动的小孔，如图3所示.

试通过必要的无损测量确定下列各量的数值并估计它们的误差：

图3 试题2实验装置示意图

i.含小球圆筒的质心位置，需给出实验方案示意图.（1.0分）

ii.距离z.（3.5分）

iv.重力加速度g.（2.0分）

实验装置如图4所示：1个内含小球的圆筒，1个带有细针的基板，1个针帽，1把直尺，1个停表，1段细线，1支铅笔和1卷胶带.图3中xC是圆筒顶端到质心的距离，R是转轴到质心的距离.

图4 试题2实验装置实物图

提示：

1）对于该物理摆（即复摆），[（M＋m）R2＋这里IC是上述含小球圆筒相对质心的转动惯量，θ是角位移.

2）长为L、质量为M的圆筒，绕经过质心且垂直于圆筒中轴线的转轴旋转，其转动惯量可近似表示为

3）平行轴定理为I＝IC＋Mx2，这里x是转轴到质心的距离，M是物体的总质量.

4）球可当作质点处理，位于圆筒中轴线上.

5）圆筒质量分布均匀，两端封帽的质量可忽略不计.

3 试题解答

3.1 试题1解答

3.1.1 校准

将式（1）写成：

表2 弛张振荡器频率与电容的关系

评分标准：采用了2个电容并联得0.4分；至少有1个电容值超151pF得0.4分；画出－C

图5 －C校准曲线

3.1.2 决定平板电容器的几何形状

经简单分析即可得到不同图案的平板电容器的电容量与上极板位置的关系，如图6所示.

图6满分为1.4分.对图案1，要求周期为2w（0.1分），电容随上极板位置要线性上升或下降（0.3分）.对图案2，要求周期为2w（0.1分），峰形为抛物线型（0.2分），若峰画成尖的或类似高斯型可给0.1分，空白区（w～2w间）可画成平的或略微下降或升高（与相邻峰的升降一致），后续的空白区高度亦可以比前一空白区略微下降或升高（与相邻峰的升降一致）（0.2分）.对图案3，要求峰区宽度为w，总周期为3w（0.2分）.对所有图案都要求峰值高度要依上极板位置坐标的取法而逐渐下降或上升（0.2分）.

图6 不同图案的平板电容C与上极板位置D的关系

将待测电学黑盒子作为电容接入弛张振荡器，测量不同上极板位置下的弛张振荡器振荡频率f并由此算出对应的电容值，结果见表3.这里将上极板能拉出的极限位置取为位置零点.由表3可画出电容与上极板位置的关系，见图7.

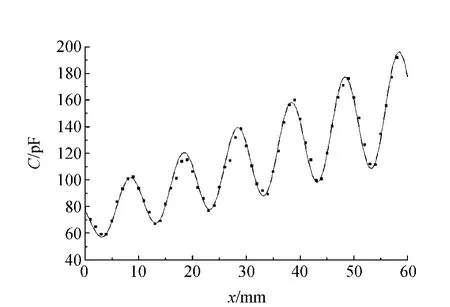
图7 电容值与上极板位置的关系

表3 上极板位置与电容的关系

图7中电容极小位置对应上下极板完全没有交叠时的情况，此时仍然存在分布电容，且分布电容随上极板被推入而增加.

对比图7与图6可以得出结论：黑盒子内电极的形状应与图案1的相同.根据曲线的周期，可以定出参量w＝5.0mm.从表3中（或从图上）可以读出5个电容极大点的值，记入表4.

表4 电容的峰值

由表4作图或用线性拟合的方法可以得到每对齿片构成的电容值为ΔC＝19.2pF.根据平板电容公式

将εr，ε0和d的值代入，并注意单一齿片的面积A＝wb，可算出：b＝58mm.

评分标准对物理概念、实验技能和测量结果的精度和质量都有要求.

根据学生是否知道式（3）、是否知道图6～7中相邻电容峰值差ΔC代表1对齿片叠合时的电容和是否知道由ΔC来求b，要么给1.5分，要么给零分.

表3的数据部分占0.4分，单位占0.2分.图的水平和竖直范围均要覆盖图纸相应宽度的一半以上（各0.1分），水平和竖直轴单位要正确（0.1分），数据点标记要正确（0.2分）.

图7中如含有5个或5个以上峰得0.5分，含3～4个峰得0.3分，低于3个峰不得分.上极板位置测量间距取1mm得0.4分，2mm得0.2分，大于2.5mm不得分.

由图7求ΔC时，如果仅用相邻2个峰值差，得0.1分；仅用首尾2个峰差，得0.3分；或用到3个以上的峰差平均值，得0.3分；由4个以上的点用直线拟合的方法，得满分0.5分.尽管按电容谷值差来求ΔC是错误的，但依然按上面的评分标准给分.

w的测量值在4.90～5.10间得0.3分，超出此范围不得分.b的值在50～80mm间得0.2分，超出此范围不得分.结果单位错漏和有效数字超过3位各扣0.1分.

3.1.3 数字卡尺的分辨率

由表3可知，f≈5kHz对应着多个上极板位置.欲求可以分辨的最小距离，应该取频率随上极板位置变化最陡峭的位置来考察.根据表3的数据，上极板位置取36.2mm或41.5mm附近均可.取34.0～38.0mm间5个点作C－x线性拟合，可得斜率为γ＝17.1pF／mm.由式（2）和频率计的分辨率Δf＝0.01kHz，可得

虽然不是太严格，但可接受的另一种方法是：使上极板位于36mm附近，轻微改变上极板位置，测量振荡频率的改变，再由频率分辨率求出位置分辨率.由位置改变2mm频率变化1.33kHz以及频率分辨率为0.01kHz，可推得

如理解电容C与上极板位置间有线性关系得0.3分.Δf取值在0.01～0.05kHz间得0.1分.得到图7中适当区域电容或频率与上极板位置线性拟合的斜率得0.3分.卡尺分辨率的最后结果落在（1.5～1.8mm／kHz）Δf内得0.3分；落在（1.0～1.4mm／kHz）Δf或（1.9～2.2mm／kHz）Δf得0.1分；其他值不得分.结果的单位有错漏和有效数字多于3位各扣0.1分.

3.2 试题2解答

3.2.1 xC的测量

可直接用直尺单次测量测得：L＝（30.0±0.1）cm.

将圆筒用细线吊起或用一刃状物（如基板端的针或1个棱）托起，仔细调整悬挂或支承点位置使圆筒处于水平状态.此时的悬挂点或支承点就对应质心位置.多次测量出此点距圆筒一端的距离，并做统计分析可得xC＝（17.8±0.1）cm.

用图示意出测量方法可以得0.4分.测量次数大于3次得0.2分.测量值与标准值差别在0.2cm内得0.2分，由多次测量得到的不确定度在0.3cm内得0.2分，用单次测量得到不确定度在0.1～0.2cm间得0.1分.

3.2.2 其他参量的测量

题目并未给出圆筒的直径，意味着可将圆筒视为细杆.根据质心定义有

如以O为支点，让圆筒竖直作小角摆动（复摆），则摆角θ满足运动方程

其中，

为整个圆筒相对过质心垂直于中轴的转动惯量.

式（7）是一简谐振动方程，其周期为

式（9）亦可写为

用胶带纸将基板固定在桌子边沿，使细针伸出桌沿.依次将圆筒上的不同小孔插入细针，测量其摆动周期.将摆动周期T和小孔距圆筒一端的距离xC－R记入表5中.

表5 圆筒摆动周期T的测量数据

图8给出了由表5中数据得到的T2R－R2关系图.

图8 T2 R－R2关系图

对图8作线性拟合得到了相关系数r＝0.999 83，截距α＝（3.10±0.05）s2·cm和斜率β＝（0.041 4±0.000 7）s2·cm－1，截距和斜率的误差由相关系数算出.由此可得：

联立式（6），（8）和（12）可解得

由此可解得

再由式（14）和（6）可得

其中的误差由各方程中系数的变化范围用数值方法求得.

评分要考虑物理概念、实验技能和测量精度3个方面.物理概念方面的得分点，要么给满分，要么不给分.其中，给出摆动频率或周期的表达式得0.4分，给出能通过作图获得所需参量的直线方程得1.0分，给出相对于质心的转动惯量式（8）得0.4分，给出式（6）得0.4分.实验技能方面：测量表格包含T和R的内容各得0.2分，单位正确得0.2分；图线在横轴和纵轴方向均能覆盖图纸一半以上的区域得0.3分，不能则不得分.正确和部分正确地画出实验点分别得0.4分和0.2分，单位正确得0.3分.单次测量周期≥10个得0.5分，≥7个得0.3分，＜7个周期不得分；对每个转轴位置测量次数≥3次得0.3分，＝2次得0.1分，只测1次得0分.转轴位置的个数≥10得0.5分，≥8得0.4分，≥5得0.3分，＜5不得分.给出能求出z和M／m的2个方程得0.2分，由2个方程求出z和M／m得0.2分.实验精度方面：g的值在9.68～9.88m／s2间得0.6分，在9.58～9.67m／s2或9.89～9.98m／s2间得0.3分.z的值在25.9～26.2cm间得0.6分，在25.5～25.8cm或26.3～26.6cm间得0.3分.M／m的值在2.6～2.8之间得0.6分，在2.5～2.59或2.81～2.9之间得0.3分.g，z和M／m的误差估计方法合理各得0.2分，相应前驱误差（precursor errors）估计方法合理各得0.1分.Δz≤0.4cm或Δ（M／m）≤0.15即得0.4分，否则此项不得分.

评分标准对测量精度的要求显然是太高了，就连赛会所提供的标准数据在许多项上也都达不到要求.

4 结束语

本次竞赛的考题在原理和实验线路上都没有多少困难，但对实验细节，特别是测量的精度有较高要求，主要考察的是实验者的基本实验素养和技能.中国学生习惯上重物理内容轻实验技能、重实验方法轻测量精度，所以在本次竞赛中实验成绩并不理想.在第一题中，有4位中国学生都未能将所给电容并联以得到更多和更大的电容值，并因此被扣了0.8分.第二题的结果更不理想，最高得分也仅有8.5分.其中一位同学的g，z和M／m的测量值和误差全部在要求范围之外，仅此，就被扣掉了2.5分.今后，还应进一步加强对中国学生实验素养和技能方面的培养和训练.

[1] 吕斯骅，段家忯.新编基础物理实验[M].北京：高等教育出版社，2006.

[2] 马秀芳，沈元华.第八届亚洲物理奥林匹克竞赛中实验考题的分析[J].物理实验，2007，27（12）：29－33.

[3] 廖慧敏，荀坤，陈晓林.第12届亚洲物理奥林匹克竞赛实验题介绍与解答[J].物理实验，2011，31（10）：16－25.

[4] 荀坤，王若鹏，陈晓林，等.第41届国际物理奥林匹克竞赛实验试题简介[J].物理实验，2010，30（11）：21－28.

[5] 荀坤，王若鹏，陈晓林.第40届国际物理奥林匹克竞赛实验试题简介[J].物理实验，2010，30（1）：20－27.