动感体验为初中数学课堂增添活力

☉江苏省南通市通州区金沙中学 吴才东

动感体验为初中数学课堂增添活力

☉江苏省南通市通州区金沙中学 吴才东

利用动画演示可以创设、模拟多种与教学内容相适应的情境；为学生从事数学探究提供重要的工具；是从根本上改变数学学习方式的重要途径之一.本人在新人教版八年级下册19.2.3正方形（1）的教学设计中着眼于从学生动手操作开始，引导学生通过操作、观察、思考、归纳等形式，让学生自主参与学习活动.下面就本课教学过程中选取的某些多媒体技术与教学内容的整合点作简要的阐述：

一、组织学生动手实验，利用多媒体，引领学生构建概念

利用动画演示几何图形的空间运动和空间演变的过程，帮助学生通过观察、比较、分析、综合转入理性思考，可以有效地提高数学学习的效率，提高学生数学思维的能力.

本节课一开始创设了学生喜欢而又熟悉的折纸活动，如何将一张矩形纸片折成一个最大的正方形，使学生直观感知正方形是特殊的矩形，初步建立了正方形是一组邻边相等的正方形的表象.在充分感知的基础上，再利用几何画板做动态演示，让同学们观察并思考得出结论：正方形是一组邻边相等的矩形，在模仿折纸动态演示过程中，利用几何画板反复出现三个直角（∠A、∠B、∠F）闪烁，从而让学生清楚地知道正方形是矩形，在此基础上再让学生注意到折纸时是将宽边AB折到长边BC上，并借助几何画板让重合的那组邻边AB和BF闪烁，让学生感悟到正方形是一组邻边相等的矩形.然后又设计了一个动手实验，即怎样将一个菱形的衣帽架变为正方形衣帽架，使学生直观感知正方形与菱形的联系.接下来又用几何画板设计了一个动态演示过程，将菱形的一个角变化为直角得到了正方形，在此过程中几何画板上显示的原菱形四条边大小的数据始终不变，从而让同学们清楚地认识到正方形是菱形，在将∠BAC变为直角时，采用闪动效果让学生感悟到正方形又是一个角是直角的菱形，为下面说明一组邻边相等且有一个角是直角的平行四边形作铺垫.这样，顺利引出正方形的概念，突破了难点并为下面研究正方形的性质做好了准备，这样处理，既使得学生的体验过程更丰富，感受更深刻，又注意渗透从一般到特殊的研究问题的方法.不仅能够吸引学生的注意力，而且能够潜移默化地培养学生自主探索、研究问题的数学能力.

二、指导学生设计变式，启发思维，引发学生自主探究

很多数学知识、方法之间往往存在必然的联系，由已学知识拓展新知识的数学教学应该关注如何让新知、新法成为已知内容合乎逻辑的发展结果，成为已知内容的自然延伸.借助多媒体演示帮助学生把握知识的生长点，思维的连接点，方法的迁移点，为学生搭建好自主探究、自主构建的平台.为了训练和培养学生运用知识解决问题的能力，在课堂中进行变式训练是十分必要和有效的，在变式训练中，学生可以放开手脚自己去想象、琢磨，从而有机会从多角度、多侧面、多层次、多结论等方面去认识知识，学生的创造性思维得到了发展，思维活动的质量也得到了提高.通过这些变式，原题便具有了“活力”，例题的功能也可更充分地发挥.

例1 求证：正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

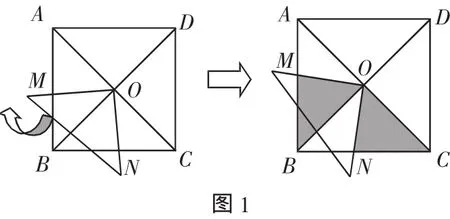
对例1的处理：因为题目较为简单，出示例题后，由一名学生直接口述解决问题.然后，设计了两个变式，变式1：如图1，将△BOC绕点O转动，边OB、OC分别与AB、BC交于点M、N.试问：OM与ON是否相等？变式2：若正方形的边长为1，求四边形OMBN的面积.变式1将△BOC绕点O旋转，边OB、OC分别与AB、BC交于点M、N.问：OM与ON是否相等？教学时引导学生学会将复杂图形分离成基本图形.然后，借助几何画板对图形做一些变化，用阴影部分并闪烁突出两个全等的三角形，使学生了解到在转动过程中△BOM与△CON始终是全等的，为变式2的问题解决埋下了伏笔.待变式2解决后作一学法指导：在计算不规则图形的面积时，通常通过割补法将不规则的图形转化为规则图形来计算.通过变式，引导学生灵活运用正方形的性质解决问题，使学生成为学习的主体，使课堂充满活力.

三、鼓励学生参与活动拓展，积累经验，培养学生创新能力

数学教学的重要目标是帮助学生积累数学学习经验，使之在数学学习上具有可持续发展性，以不断提高学生数学素养.学生学习数学的能力是学生不断经历、体验各种数学活动过程的结果.数学活动经验需要在“做”的过程和“思考”的过程中积淀，也需要学生在数学学习活动过程中自我认识、自我感悟并形成内化而逐步积累的.鼓励学生有效地参与数学探究活动，使学生经历数学的发生发展过程，是学生积累数学活动经验的重要途径.

接下来设计了例2，如图2，正方形ABCD中，对角线AC、BD的交点为O，E是OB上的一点，DG⊥AE于G，DG交OA于F.求证：OE=OF.

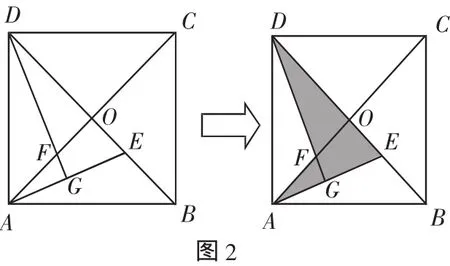
先让学生思考后，认识到解决问题的关键是证明△AOE与△DOF全等，并由学生板演，再利用几何画板将这两个三角形加上阴影闪烁效果使学生进一步明确解题的关键.然后借助几何画板对图形作动态变化：移动点E到DB的延长线上，得变式1：若点E在DB延长线上（如图3所示），DG⊥AE交EA的延长线于G，DG延长线交CA延长线于F，其他条件不变，OE=OF还成立吗？若成立，请给予证明；若不成立，请说明理由.（学生口述过程）

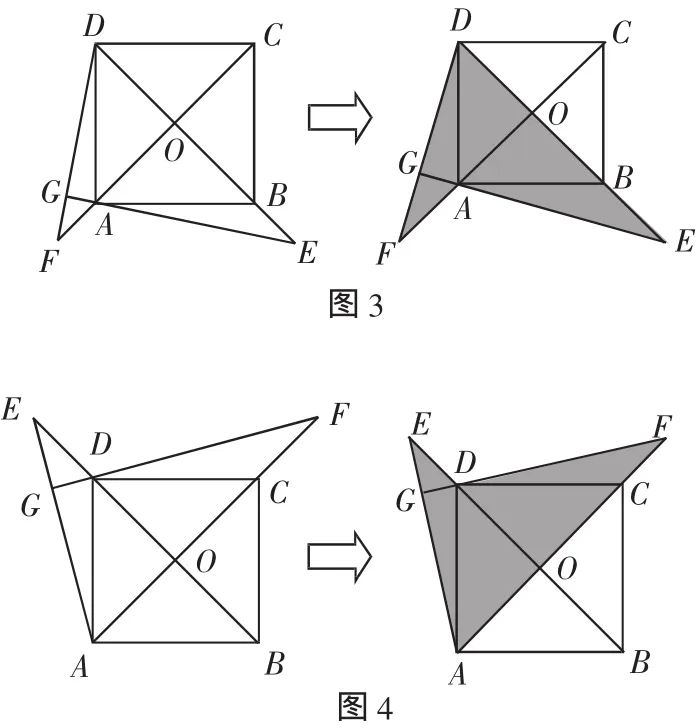
此时引导学生思考刚才所证明的△AOE与△DOF是否全等，这时利用几何画板给这两个三角形加阴影闪烁使问题解法明朗化.接下来，再利用几何画板将点E移动到BD的延长线上得到变式2，变式2：若点E在BD延长线上（如图4所示），DG⊥AE于G，GD延长线与AC延长线于F，其他条件不变，OE=OF还成立吗？若成立，请给予证明；若不成立，请说明理由.学生在刚才探讨的基础上自然联想到这两个三角形依然全等，这样问题就迎刃而解了.这样处理首先调动了学生思维的积极性，其次更深层次地培养了学生的数学思维能力，拓展了他们的思维空间.

在预设正方形（1）的教学时把学生的学被确定为发现式学习，此学习方式是由学习者自己发现问题和解决问题的一种学习方式，有利于培养创新意识和合作精神.本人在实施教学时就根据学生的这一学习特点设计相应的教学方法以及教学的组织形式.在指导学生学习概念和原理时，只给他们一些事实和问题，如通过折纸实验及变式训练等让学生积极思考，独立探索，自己发现并掌握相应的原理和规则.对此教学过程中正方形的概念、性质等均没有直接给学生，而是在教师创设的动手实验及几何画板演示中让学生发现而获得.创设富于启发性的问题，开发学生的探索能力和培养学生的合作精神.设置具有层次性的问题，借助于几何画板的直观性和灵活性的作用，让学生主动学会从复杂图形中识别、分解出基本图形，使问题由难变易，化抽象为具体，花较少的时间，掌握了更多的知识，收到了“事半功倍”的效果，学生真正学得轻松.

1.义务教育数学课程标准（2011年版）.北京：北京师范大学出版社，2012.