基于分块过完备稀疏表示的多聚焦图像融合

陈垚佳，张永平，田建艳

(1.太原理工大学 信息工程学院，山西 太原030024;2.宁波工程学院 电子与信息工程学院，浙江 宁波315211)

由于光学成像机理的限制，单幅图像所能捕捉到的信息量有限，不能保证同一场景里的背景与目标都均匀清晰。通过对同一场景进行多聚焦拍摄，可以得到多幅不同聚焦点的图像。多聚焦图像融合技术就是利用这组多聚焦图像的互补和冗余信息，得到一幅可信度高、更为人眼视觉所接受的新图像。在医学、遥感、计算机视觉、天气预报及军事目标识别等方面图像融合技术都得到广泛的应用。

融合技术可分为像素级、特征级、决策级三个层次的融合。目前的研究主要以像素级融合为主，其融合方法主要分为两类:空间域方法比如像素的加权平均、伪彩色映射、非线性方法、贝叶斯优化方法、人工神经网络法［1］等和变换域方法如金字塔分解、小波［2-5］、曲波［6］、轮廓波［7］等多分辨力变换以及经验模式分解［8］、ICA变换［9］、非负矩阵分解［10］等。

基于变换域的图像融合作为一种有效的融合技术得到快速发展。这种融合方法首先图像分解到另一个变换域，对变换域系数按照一定规则进行融合，最后利用逆变换重构融合图像。图像变换主要是基于小波、曲波、轮廓波等多分辨力变换。这类变换是在完备基上对图像进行表示的，不能对图像很好的稀疏表达。近年来稀疏表示被应用于图像处理与分析领域，如图像去噪［11］、超分辨力［12］、修复［13］以及人脸识别等，它是在过完备基上对信号进行表示的，具有更好的稀疏表达能力。

文献［14］中提出一种基于过完备稀疏表示的多聚焦融合算法，其本质是基于每个像素领域过完备稀疏表示然后进行融合、重构的方法，计算量较大。本文充分考虑到多聚焦图像融合的特性，提出一种基于分块过完备稀疏表示的多聚焦图像融合算法。首先将源图像分块，利用稀疏模型分解块图像，然后采用加权平均的融合规则对稀疏表示系数进行融合，最后由融合系数与字典重构图像。实验表明，该算法得到的融合图像在主观视觉和客观质量上都取得较好的效果。

1 稀疏域模型

稀疏表示问题可描述为式(1)，由于式(1)是NP问题，所以往往转化为式(2)中的近似问题来求解

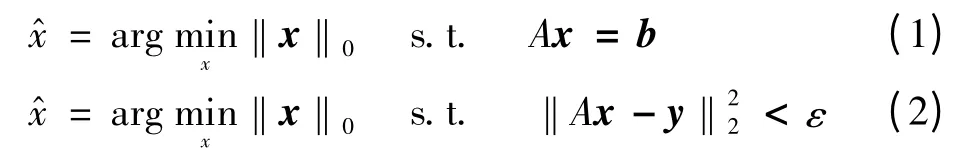
式中:‖x‖0为x的l0范数，即向量x中非零元素的个数，为信号x在过完备字典A上的稀疏表示。

一般情况下自然图像的数据信息也具有冗余性，因此可以在冗余字典上进行稀疏表示。如果将图像信号看做一维向量b，其稀疏表示是指信号b在冗余字典A下的低维投影，投影系数即为稀疏表示系数x。

1.1 过完备字典的构建

过完备稀疏表示问题中，选取的过完备字典是否合适关系到表示信号被表示的稀疏性。针对不同结构与特征的图像，应采取不同形式的字典或者基函数。过完备字典的构建方法可以划分为两类。

1)根据数学模型来构建字典。由于其模型较简单，正交和双正交变换的字典构建方法一度占据主导地位。然而研究表明这种构建方法得到的字典不能保证信号表示的稀疏性，进而影响信号的重构准确度。文献［15］提出利用适合刻画图像几何边缘的bandlet基、适合刻画纹理的Gabor基、适合刻画轮廓的Curvelet基等不同形状的基函数组合构建字典。采用该类方法构建的字典优势在于适用范围比较广。

2)根据样本来设计字典。可以通过训练样本来学习适合某一类信号特征的字典，以确保信号表示的稀疏性。目前字典学习的算法有最大似然法、最优方向(MOD)法、最大后验概率法、组合正交基学习算法、广义PCA算法。能与现今的稀疏分解算法兼容的常用方法是ELAD于2006年提出的K-SVD学习算法［16］。该方法交替执行信号在当前字典的稀疏表示与原子的更新过程，来达到学习字典的目的:

(3)D(J-1)中每列原子更新，对于第k(k=1，2，…，K)列原子dk更新步骤如下:

①定义步骤(2)中使用第k列原子的标志集合:ωk={i 1≤i≤N(i)≠0}。

③根据ωk中标志元素选出Ek的部分列得到。

(4)返回步骤(2)，J=J+1。

为了探讨字典维数对本文算法融合结果的影响，在给定学习对象数量的条件下，学习不同维数的字典。在后面的研究中，将利用所构建的字典探讨其对融合结果的影响。

采用50幅自然图像进行8×8的分块，分块处理后的块图像作为输入图像，通过K-SVD字典学习算法得到维数为64×64，64×128，64×256的过完备字典，设定迭代次数为J=50，字典图像如图1所示。

图1 不同维数过完备字典图像

1.2 稀疏表示方法

其次是设计快速有效的稀疏分解算法。目前有三类典型方法:匹配追踪算法、基于l1范数算法、迭代收敛算法。匹配追踪算法以贪婪算法为核心的最简单直接的算法。本文的融合算法中，以误差作为循环停止条件，采用正交匹配追踪(OMP)算法来对源图块进行稀疏表示［17］，算法如下:

1)初始化。误差ε，字典D，X0=0，r0=b=∅。

2)从冗余字典中选出与被表示信号b内积最大的原子di，即di=

5)计算误差rk=b-。

6)如果rk≥ε，返回步骤2)。反之，结束循环，输出的即为所求的稀疏系数。

图像稀疏表示即是将待融合图像采用正交匹配追踪算法在经过K-SVD算法学习的过完备字典上进行稀疏表示。在稀疏分解过程中，需要设置分解过程的循环停止参数ε。ε过小会影响融合图像的分解精度，当ε过大时，迭代次数随之提高，计算量也会随之增大。因此该参数要慎重选择。文献［14］探讨了ε在过完备稀疏表示图像融合算法中的对图像质量的影响，证实了以上的结论。

2 基于稀疏域的多聚焦融合算法

2.1 基于稀疏表示的图像融合框架

稀疏表示具有在过完备字典上对自然图像的稀疏表达能力。将稀疏表示引入图像融合，提出一种图像融合算法，算法流程图如图2所示。

1)源图像预处理。假定待融合图像为严格匹配图像，首先将图像归一化，如图3，然后将源图像进行8×8分块处理，并且将每个图像块像素整合成一维列向量。

2)稀疏分解。将图像块对应的一维向量在冗余字典上进行稀疏分解，每个图像块对应得到两组稀疏表示系数。

3)稀疏系数融合。每个块对应的两组稀疏系数按照一定的融合规则进行融合，获得待重构系数。

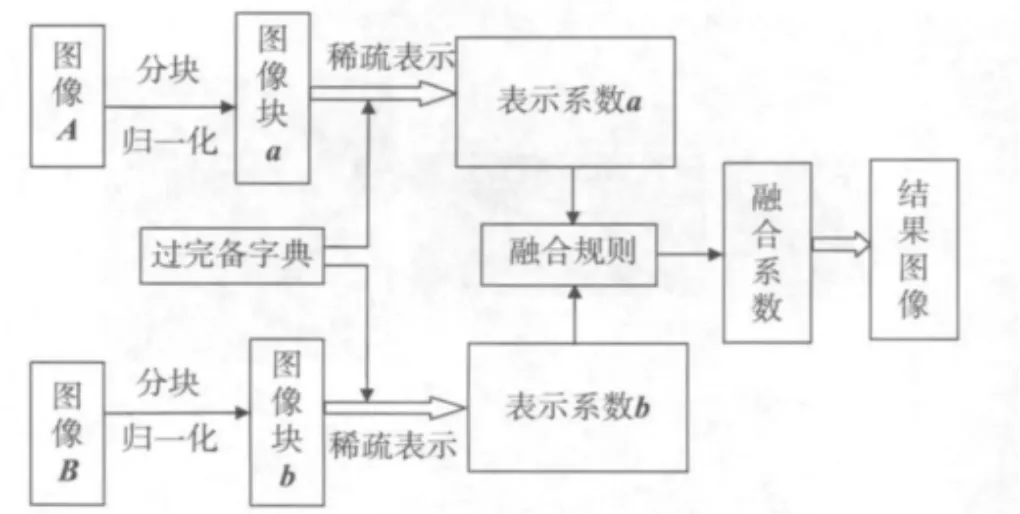
图2 基于过完备稀疏表示的融合算法框图

4)稀疏重构图像。重构是分解的逆过程。结合融合系数与冗余字典按照图3进行重构，得到最后的融合图像。

图3 源图像分块与重构示意图

2.2 融合规则

融合规则是图像融合算法中决定最终融合质量的关键步骤［18］。常用的融合规则有绝对值最大以及平均等方法。如果按照绝对值取大规则来融合，融合结果会出现很多块效应，影响视觉效果。因此本文选用平均方法的融合规则，对系数简单的取平均，会降低融合图像对比度，丢失部分细节信息。

综合以上因素，本文采用加权平均的规则进行融合。图像块稀疏系数的l1范数越大，携带的信息量就越多。基于以上理论，融合系数由式(3)计算

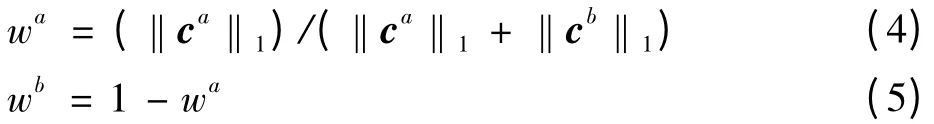
式中:ca，cb为源图像分别对应图像块稀疏系数向量。

3 实验与性能评价

3.1 不同算法的对比试验

采用严格配准的两组大小为256×256的多聚焦图像进行实验，验证本算法的有效性。同时与基于小波分解的传统融合算法、基于稀疏表示的融合规则取系数平均算法对比。其中小波融合方法中小波分解层数为3层，小波基选取bior2.4，融合规则为低频系数取平均、高频系数取大。基于稀疏表示的方法中，用图像稀疏表示分解图像，融合规则为系数取平均方法。图像融合结果分别如图4。由图可见，本文算法的融合图像整体效果更好。

由于不存在标准图像，采用信息熵(Entropy)、互信息量(MI)、边缘评价因子(Q)、空间频率(SF)这四个指标来评价实验结果。

1)信息熵是衡量图像包含的信息量丰富程度的一个重要指标，被定义为

式中，pi为图像的直方图，即灰度值等于i的像素个数与图像总像素个数之比。融合图像熵值越大，表示其包含的信息量越多，融合质量越好。

2)互信息量MI被定义为)

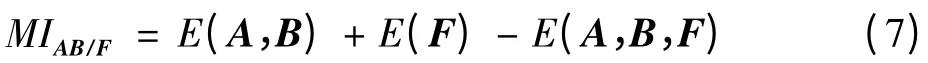
式中，E()为图像的互信息量，可由图像的归一化联合灰度直方图得到。互信息量MI越大，意味着融合图像F从源图像中继承的信息越多，融合效果越理想。

3)空间频率是直接反应图像的清晰度的指标，是被作为衡量图像整体视觉效果的标准，融合图像的此指标值越高，意味着融合结果图像效果越好。对于大小为M×N的图像，其空间频率定义为

其中RI和CI分别为行频率和列频率，被定义为

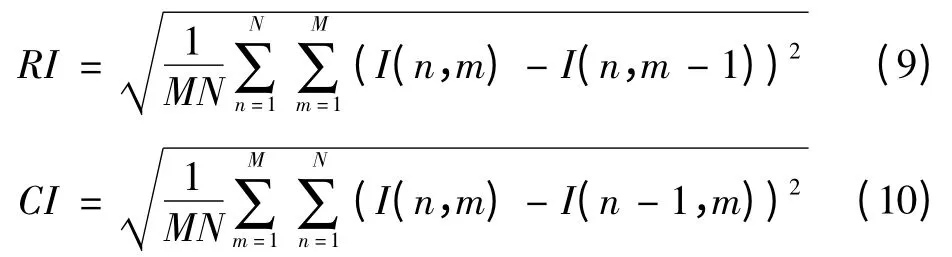
4)采用结构相似度Q来评价实验结果

式中:s(A|ω)代表源图像A中具有方差、边缘等显著特征的信息量。同样指标Q值越大，表示融合图像保留源图像的边缘信息越多，融合质量越高。

表1为不同算法融合结果的指标。从表1可以看出，基于稀疏表示融合图像的互信息量指标优于传统小波融合算法。使用过完备稀疏表示，融合规则采用系数平均的算法融合结果结构相似度指标不如传统小波算法，但是采用本文提出的加权平均融合规则，其结构相似度的性能指标得到极大的改善，且优于传统小波算法。

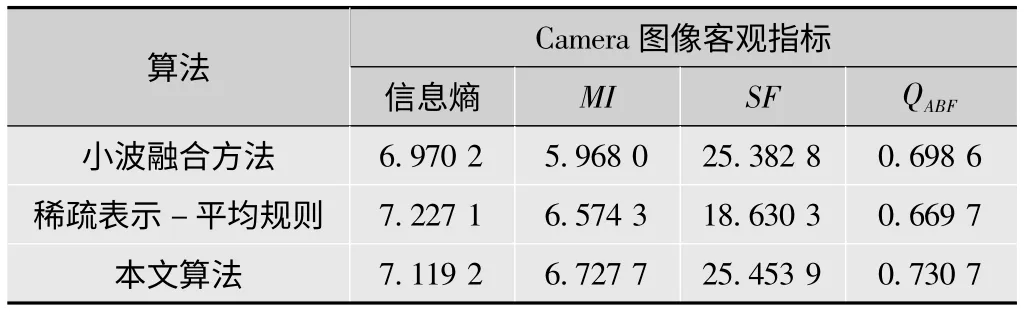
表1 不同算法融合图像客观指标

3.2 字典维数对图像融合质量的影响

文献［14］已经对图像分块窗口大小、正交匹配追踪(OMP)算法中的残差等因素对融合质量的影响进行了研究。本节通过实验探讨过完备字典维数对图像融合结果的影响。将上文中已经学习到的不同维数(64×64，64×128，64×256)的字典均应用到本章提出的融合算法中，融合结果同样由信息熵(Entropy)、互信息量(MI)和边缘评价因子(Q)以及空间频率(SF)4个指标来评价，如表2所示。

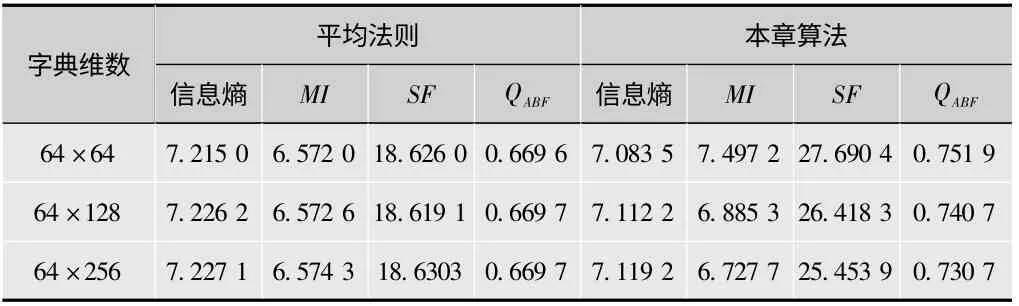
表2 不同维数字典的融合图像客观评价结果

从表2中的指标可以看出，在平均融合规则下，过完备字典维数越高，融合性能越好。在本章算法的加权融合规则下，在不同维数的过完备字典上表示的融合性能也有所区别。但不同的是，选取较低的字典维数反而在多数指

标下得到较好融合性能。这表明，各种融合算法的性能与字典维数的相关性还有待进一步研究。

4 结论

笔者提出一种基于分块稀疏表示的多聚焦融合算法。首先将源图像无重叠像素分块，并采用稀疏域模型将分块图像进行表示，得到两组稀疏系数。使用加权平均的融合规则得到融合系数。通过稀疏逆变换重构图像。实验表明无论是从主观视觉还是客观指标来评价，该算法取得了较好的融合效果，且由于传统的小波融合算法。同时探讨了过完备字典在该方法中对图像融合质量的影响。实验表明过完备字典的优劣是影响融合结果的一个重要因素。构建一组更适合于多聚焦图像的过完备字典，使其具备较强提取图像边缘的能力，在其上的表示系数能够更好的区分出清晰与模糊区域，对于多聚焦图像融合算法亦是非常重要。

［1］LI S T，KWOK J，WANG Y N.Multifocus image fusion using artificial neural networks［J］.Pattern Recognition，2002，23(8):985-997.

［2］XU L，ROUX M，HE M Y，et al.A new method of image fusion based on redundant wavelet transform［C］//Proc.VIE 2008.［S.l.］:IEEE Press，2008:12-17.

［3］LEWIS J J，CALLAGHAN R J O，NIKOLOV S G，et al.Pixel-and regionbased image fusion using complex wavelets［J］.Information Fusion，2007，8(2):119-130.

［4］郭敏，任娜.基于小波变换与块分割的多聚焦图像融合［J］.云南大学学报:自然科学版，2008，30(3):251-255.

［5］LI H，MANJUNATH B S，MITRA A A.Multisensor image fusion using the wavelet transform［J］.Graphical Models Image Process，1995，57(3):235-245.

［6］杨俊，赵忠明.基于Curvelet变换的多聚焦图像融合方法［J］.光电工程，2007，34(6):67-71.

［7］ZHANG Q，GUO B L.Mutifocus image fusion using the nonsubsampled contourlet transform［J］.Signal Processing，2009，89(7):1334-1346.

［8］CHEN S H，SU H B，ZHANG R H.Improving empirical mode decomposition using support vector machines for multifocus image fusion［J］.Sensors，2008，8(4):2500-2508.

［9］MITIANOUDIS N，STATHAKI T.Pixel-based and region-based image fusion schemes using ICA bases［J］.Information Fusion，2007，8(2):131-142.

［10］ZHANG S，CHEN J，MIAO D D.An image fusion method based on WNMF and region segmentation［C］//Proc.PACIIA’08:vol 2.［S.l.］:IEEE Press，2008:282-285.

［11］ELAD M，AHARON M.Image denoising via sparse and redundant representations over learned dictionaries［J］.IEEE Trans.Image Process，2006，15(12):3736-3745.

［12］YANG J C，WRIGHT J，HUANG T.Image super-resolution via sparse representation［J］.IEEE Trans.Image Process，2010，19(11):2861-2873.

［13］MARIAL J，ELAD M，SAPIRO G.Sparse representation for color image restoration［J］.IEEE Trans.Image Process，2008，17(1):53-69.

［14］YANG B，LI S T.Multifocus image fusion and restoration with sparse representation［J］.IEEE Trans.Instrumentation and Measurement，2010，59(4):884-892.

［15］PEYRE G.Best Basis compressed sensing［J］.Lecture Notes in Computer Science，2007，4485:80-91.

［16］AHARON M，ELAD M，BRUCKSTEIN A M.The K-SVD:an algorithm for designing of overcomplete dictionaries for sparse representations［J］.IEEE Trans.Image Process，2006，54(11):4311-4322.

［17］ROSENBLUM K，ZELNIK-MANOR L，ELDAR Y C.Dictionary optimization for block-sparse representations［EB/OL］.［2011-06-01］.http://arxiv.org/pdf/1005.0202.pdf.

［18］李亚春，武金岗，王净.小波变换图像融合规则性能的分析研究［J］.计算机工程与应用，2010，46(8):180-182.