基于非活跃关系的合作行为演化研究①

林敏

（北京科技大学 经济管理学院，北京100083）

1 引言

合作行为在自然界和社会的各种系统中都普遍存在，如社会经济领域中的产业联盟、跨组织合作研发、知识共享等。学者们试图找出合作行为涌现的原因。其中，演化囚徒困境博弈是研究合作行为的一个重要方法。Axelord和Hamilton以囚徒困境博弈为基础建立模型，采取模型推理和计算机演算，研究了合作在一个利己群体中是如何开始并最终稳定下来的［1-2］。有学者提出雪堆模型（snowdrift game），用以解决囚徒困境模型在估计报偿系数方面的缺陷［3-4］。这两种模型都可被看成是描述两个个体之间相互作用的矩阵博弈（matrix game）。博弈个体的基本策略空间是（合作，背叛）。如果双方合作，则两者都会得到收益R；如果双方都选择背叛，则两者都要受到惩罚P；如果一方合作、另一方背叛，则背叛者会得到收益T（也可将该参数理解为个体采取欺骗策略的诱惑），而被骗一方将会损失S。在囚徒困境模型中，这些报偿参数满足T＞R＞P＞S；而雪堆模型中，则T＞R＞S＞P。这些报偿参数给那些希望获得最大收益的个体提出了一个难以解决的困境：无论对方采取什么策略，个人采取欺骗策略都会获得最高收益；但是，若两个人都采取欺骗策略，则他们都将获得较差收益。所以，在混合群体（well-mixed population）中，经过博弈后最终都会涌现出相互欺骗的策略［5］；而在现实系统中，合作才是最普遍的选择——这与现实情况恰好相反。为了解释这一现象，学者们针对囚徒困境模型提出了许多改进策略。研究发现，当引入诸如亲缘选择（kin selection）机制［6］、针锋相对（tit-for-tat）机制［7］以及自愿参与（voluntary participation）机制［8-10］等机制时，系统中会出现并保持合作行为。

Nowak和May提出的空间博弈（spatial game）［11-12］是保持系统内合作行为的重要方法。研究发现，空间结构在很大程度上可以加强系统的合作行为［13-16］。在结构化的系统中，合作者会组成集团（cluster），并且集团内部相互合作获得的收益能够抵抗与欺骗者博弈所导致的损失，由此可以维持合作行为的稳定。基于这种认识，很多学者将研究视角转向空间结构对合作行为的影响上［17-21］。Santos和Pacheco基于具有无标度（scale-free）性质的网络研究了演化博弈问题［22-25］。研究结果表明，具有异质性的网络结构可以加强系统的合作行为，也即长期的合作策略可以抵抗短期的欺骗行为。

博弈模型反映的是社会经济系统中普遍存在的竞合现象，如企业间的竞争与合作、产业联盟、创新网络、知识共享主体间的竞合行为。然而，在已有的空间演化博弈研究中，系统的结构通常是确定的，相互关联的个体每轮都进行博弈。这与现实情况有较大的出入。首先，资源的有限性使得主体的博弈对象是有选择性的；其次，行为主体间的关系是动态变化的，如创新网络中的创新主体间的竞合关系随时可能终止、变更或建立。鉴于此，有学者引入淬火个体冷冻机制［26-27］。但是，该模型尚存在两点不足：首先，被冷冻的个体被永久性地删除了，即对于不同的冷冻概率，系统中个体的总数是变化的；其次，被冷冻个体在整个演化过程中保持不变。为了解决以上两个问题，可以引入关系冷冻，所有个体都是活跃的，并且可以进一步引入退火关系冷冻来描述真实系统的动态结构。基于以上考虑，本文引入淬火关系冷冻机制和退火关系冷冻机制，研究群体合作行为的演化。

2 模型

在本文的模型中，网络规模N=10 000。网络中的每条边有两种可能的状态——活跃的或冷冻的。关系的冷冻机制如下：群体中的关系以概率q随机设定为活跃的，而其他连边被设定为冷冻的，因此可将q理解为系统中的活跃关系比率。这样的无序既可以是淬火的，也可以是退火的。对于淬火关系冷冻，系统结构在整个演化过程中是确定的；而对于退火关系冷冻，系统结构是随时间变化的，也即系统的结构在每一轮博弈前都发生重置。

每个个体采取如下两种策略中的一种：合作（C）或不合作（D）。本文分别用一个二维的单位向量表示个体选择合作或不合作的情况，即

每条边有两种可能的状态——活跃的或冷冻的①当个体间没有关系的作用时，关系即处于非活跃的或冷冻的状态。。个体通过当前的活跃关系与其他个体进行博弈。本文用lij表示个体i与个体j间关系的状态，且关系为活跃状态的概率为p、为冷冻状态的概率为1-p，分别用1和0表示活跃状态和冷冻状态，即

其中，p∈［0，1］。在每一轮博弈中，每个个体通过活跃的关系与其他个体进行博弈，并根据自己以及对手的策略获得收益，。其中，v（i）表示节点i的邻居个体的集合，A为收益矩阵，

在囚徒困境模型中，T=b、R=1、R=S=0；在雪堆模型中，T=1+r、R=1、S=1-r、P=0。在每一轮博弈结束后，个体将采纳跟随策略，即跟随其邻居中获得最高收益的个体的策略.

本文利用合作密度（cooperator density）和持久性（persistence）2个参数研究群体的合作行为。

（1）合作密度

合作密度是刻画系统中合作行为的最重要、最直观的参量［1-2］，它表征了系统中合作者占整个系统的比率。我们用ρc（t）表示给定时刻系统的合作密度，

若第i个个体的策略为合作，那么中括号内的第一项为“+1”，相反为“-1”。因此，中括号内的值对应于两种策略——“+2”和“0”。对每个个体求和后再除以系统尺度N及归一化参数2，就可得到系统中合作个体的比率。

ρc=0意味着系统中充满了不合作者；ρc=1表示系统中全是合作者。中间态为0＜ρc＜1，表示两种策略在系统中共存。

（2）持久性

本文用持久性P（t）表示在时刻t前没有改变策略的个体占整个系统的比例。

3 模拟结果和讨论

本文通过数值模拟研究了引入淬火关系冷冻机制和退火关系冷冻机制对合作密度和持久性的影响。在淬火关系冷冻机制中，所有的模拟结果是在10 000个时间步后取5 000步平均而得到的，并且最终结果是对128次独立的模拟取平均而得到的；在退火关系冷冻机制中，参数空间中每个点的平衡态统计结果是在10 000个时间步后取10 000步平均而得到的，并且最终结果是对1 024次独立的模拟取平均而得到的。在初始状态中，设定网络中50%的个体是合作的、50%的个体是不合作的，并且随机分布在群体中。

图1显示了淬火关系冷冻机制情况下合作密度ρc随活动边比率q变化的情况。我们可以看到，当群体中的活跃关系较少时，不同报偿值下的合作密度曲线是重合的。当群体中的关系接近0时，几乎所有的个体都是孤立存在于系统中，因此不存在博弈，个体始终保持策略不变，合作密度与初始状态ρc=50%保持一致。当活跃关系的数量增加时，系统中开始出现由几个个体组成的小集团（cluster）。在这些集团中，无论报偿参数取何值，不合作策略在系统中都占主导。因此，我们可以看到，图1中合作密度曲线在开始阶段单调递减。当活跃关系增加到一定数量后，系统中的合作行为将不再由系统结构决定，而取决于报偿参数。因此，不同报偿值下的合作密度曲线开始彼此分离：报偿参数b的值越大，则越多的人采取不合作的策略；相反，报偿参数b的值越小，则越多的人采取合作的策略。在1＜b＜1.33的区域内，最佳合作行为出现在q=1；而在1.5＜b＜2区域内，最佳合作行为出现在q=0。

图2显示了退火关系冷冻机制情况下合作密度ρc随活动边比率q变化的情况。笔者发现，在退火关系冷冻机制下，退火无序中的合作图像与淬火无序中的完全不一样。当系统中的活跃关系较少时，系统中的绝大多数集团是由几个个体组成的，在这种情况下，无论报偿参数大小如何，不合作策略都占据主导地位。由于稀释过程是退火的，因此这些由不合作者组成的集团实际上可以在系统中移动，并最终将所有由合作者组成的集团吞并。而活动边比率大时的情况则相反，此时系统中将出现大集团：若报偿参数较小，则在大集团内合作者将占据主导地位，并且由于退火无序存在，因此那些由不合作者组成的小集团逐渐被吞并，因此系统中的合作行为在小报偿参数下被增强；若报偿参数很大，则在大集团内依然是不合作者占主导，并且在退火无序的作用下系统最终演化为所有个体都是不合作者的状态；若报偿参数为中等，合作者和不合作者在大集团内共存。

图2 退火关系冷冻机制下，群体中合作密度与活跃关系比率

我们通过研究发现：在淬火稀释机制下，在1.33＜b＜1.5的区域中，当活跃关系比率为某一特定的值时，合作密度ρc出现非常陡峭的下降，我们将这一特殊的活动边比率记为q＊。本研究中，q＊=0.94。当q＜q＊时，由于系统中存在很多非活动边，集团的边界被限定，导致这些集团被局域化；当q＞q＊时，系统中形成边界不受限制的大集团。可见，转变点q＊将系统分割成了局域的、稳定的合作集团和空间混沌态两个状态。

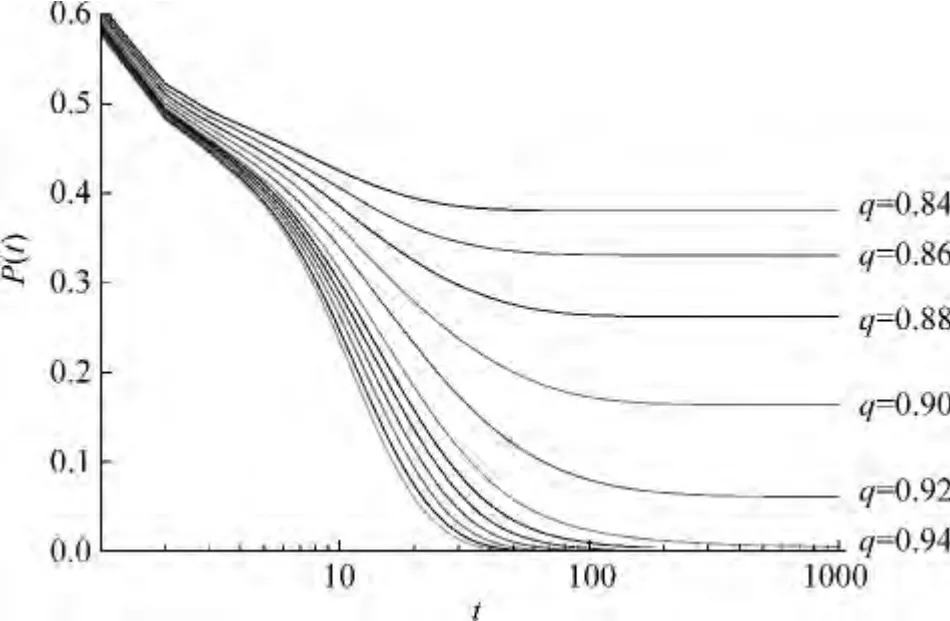
图3 系统持久性ρ（t）

为了得到在转变点处清晰的状态，本文考察系统的持久性P（t），也即在t时刻前还没有改变策略的个体的比重。图3展示了不同活跃关系比率下的系统的持久性行为。我们从图3可以看到：当q＜q＊时，随着时间的推移，持久性P（t）收敛到一个有限值，这表明系统中存在大量局域的、稳定的合作集团；当活动边比率接近临界值q＊时，系统的持久性逐渐接近0，这就意味着几乎所有的个体都在改变自己的策略，系统呈现出空间混沌，这说明集团的边界不再受到限制，进而大多数集团退局域化；当q接近临界值时，系统持久性的转变过程很明显。

4 结语

本文利用数值模拟方法，研究了引入关系冷冻机制的情况下群体合作行为的演化。研究结果表明：在淬火关系冷冻的作用下，系统在临界占有率q＊=0.94处发生局域-非局域的相变；当活动边比率在临界点之下时，关系冷冻导致的系统缺陷将合作者集团的边界固定；当活动边比率高于临界值时，这些集团被退局域化；在退火关系冷冻机制下，系统中的合作行为与淬火关系冷冻的情况完全不同，并且不发生相变。我们发现，当活跃关系比率较高时，系统中的合作行为在小报偿参数的区域内被极大地增强了。

本研究具有一定的现实含义。在社会经济生活中，企业或个人面对自身所处的环境，为了自身利益最大化会作出自己的最优决策。企业协作与竞争行为、组织中的知识共享或金融市场交易都是发生在网络上的复杂博弈。社会经济系统中如何产生合作行为，并且如何指导并调节这样的合作行为，研究这些具有重要的管理意义。例如，在知识管理研究体系中，知识共享是一个重要的研究内容。贡献知识的个体需要考虑知识共享的收益和成本，组织中的许多成员不愿意交流与共享知识是造成知识不能有效转移的重要原因，这也是一个难以解决的困局。而本研究为研究社会经济系统中多个个体（企业、组织或个人）之间的复杂博弈提供了研究工具和思路。要影响社会经济系统中的群体行为、调节竞合行为，可以采取一定的办法，如制定具体政策引导关系的形成，从而改变网络结构，最终达到管理目的。本文的研究结果对于理解并指导此类经济管理系统的合作性具有实践意义。

［1］Axelrol R，Hamilton W D.The evolution of cooperation［J］.Science，1981，211（4489）：1390-1396.

［2］Axelrol R.The Evolution of Cooperation［M］.New York：Basic Books，1984.

［3］Sugden R.The Economics of Rights，Cooperation and Welfare［M］.Oxford，UK：Blackwell，1986.

［4］Wang W X，Ren J，Chen G R，et al.Memory-based snowdrift game on networks［J］.Physics Review E，2006，74：56-113.

［5］Hofbauer J，Sigmund K.Evolutionary Games and Population Dynamics［M］.Cambridge：Cambridge University Press，1998.

［6］Hamilton W D.The genetical evolution of social behavior［J］.Journal of Theoretical Biology，1964，7（1）：1-16.

［7］Nowak M，Sigmand K.Tit for tat in heterogeneous populations［J］.Nature，1992，355（6357）：250.

［8］Hauert C，De monte S，Hofbauer J，et al.Volunteering as red queen mechanism for cooperation in public goods games［J］.Science，2002，296（5570）：1129-1132.

［9］Szabo G，Vukov J.Cooperation for volunteering and partially random partnerships［J］.Physics Review E，2004，69：036107.

［10］Szabo G，Hauert C.Evolutionary prisoner’s dilemma games with voluntary participation［J］.Physics Review E，2002，66：062903.

［11］Nowak M，May R M.Evolutionary games and spatial chaos［J］.Nature，1992，359（6398）：826.

［12］Nowak M，May R M.The spatial dilemmas of evolution［J］.International Journal of Bifurcation and Chaos，1993，3（1）：35-78.

［13］Hubermann B A，Glance N S.Evolutionary games and computer simulations［J］.Proceedings of the national academy of sciences of the United States of America，1993，90（16）：7716-7718.

［14］Nowak M A，Bonhoeffer S，May R M.Spatial games and the maintenance of cooperation［J］.Proceedings of the national academy of sciences of the United States of America，1994，91（11）：4877-4881.

［15］Nowak M A，Bonhoeffer S，May R M.Robustness of cooperation［J］.Nature（London），1996，379（6561）：126.

［16］Hauert C，Monte S D，Hofbauer J，et al.Replicator dynamics for optional public good games［J］.Journal of Theoretical Biology，2002，218（2）：187-194.

［17］Doebeli M，Knowlton N.The evolution of interspecific mutualisms［J］.Proceedings of the National Academy of Sciences of the United States of America，1998，95（15）：8676-8680.

［18］Yang H X，Wang W X，Wu Z X，et al.Diversity-optimized cooperation on complex networks［J］.Physics Review E，2009，79：056107.

［19］李南，田颖杰，朱陈平.基于小世界网络的重复囚徒困境博弈［J］.管理工程学报，2005，2（19）：140-142.

［20］林敏，李南，田亮.基于复杂网络与随机动态稀释机制的演化博弈分析［J］.系统工程，2007，25（11）：102-105.

［21］Jiang L L，Zhao M，Yang H X，et al.Reducing the heterogeneity of payoffs：An effective way to promote cooperation in the prisoner’s dilemma game［J］.Physics Review E，2009，80：031144.

［22］Santos F C，Pacheco J M.Scale-free networks provide a unifying framework for the emergence of cooperation［J］.Physics Review Letters，2005，95（9）：098104.

［23］Santos F C，Pacheco J M，Lenaerts T.Evolutionary dynamics of social dilemmas in structured heterogeneous populations［J］.Proceedings of the national academy of sciences of the United States of America，2006，103（9）：3490-3494.

［24］Santos F C，Pacheco J M.A new route to the evolution of cooperation［J］.Journal of evolutionary biology，2006，19（3）：726-733.

［25］Santos F C，Rodrigues J F，Pacheco J M.Graph topology plays a determinant role in the evolution of cooperation［J］.Proceedings of the Royal Society B，2006，273（1582）：51-55.

［26］Vainstein M H，Arenzon J J.Disordered environments in spatial games［J］.Physics Review E，2001，64：051905.

［27］Vainstein M H，Silvab A T C，Arenzon J J.Does mobility decrease cooperation？［J］.Journal of Theoretical Biology，2007，244（4）：722-728.