低强度冲击下炸药点火的数值模拟

王 晨，陈 朗，何 乐，鲁建英，2

（1.北京理工大学爆炸科学与技术国家重点实验室，北京100081；2.防化指挥学院，北京102205）

引 言

炸药在受到不同强度的冲击作用时，可能发生爆轰、爆炸、燃烧和损伤等不同程度的响应。对于强冲击下炸药的起爆规律，已经进行了比较深入的研究［1］，但对于低冲击下炸药反应机制还缺乏深入了解，而炸药事故很多与低冲击作用有关。Steven试验是一种评价低冲击下炸药安全性的试验方法，对Steven试验进行数值模拟计算，可以深入分析低冲击下炸药反应特征和规律。

Steven.K.Chidester等人建立了Steven 试验方法［2］。Chidester等人针对HMX 基炸药进行了Steven试验，获得了炸药在不同撞击速度下的响应情况，并采用点火增长模型对其反应过程进行数值计算［3］。Switzer等人［4］对PBX9404炸药进行了不同温度下的Steven试验，获得了不同温度下炸药发生反应的弹头阈值速度。韩勇［5］和代晓淦等人［6］均采用Steven试验，分析了炸药受不同作用时的力学响应。目前，Steven试验已成为研究低冲击下炸药安全性的重要方法，但由于试验测量技术的限制，主要是观察炸药反应效应，不能获得炸药反应细节。而对Steven试验数值的模拟计算，主要采用基于压力变化的炸药反应模型。而低冲击下炸药的点火主要与温度相关，基于压力的炸药反应模型对判断点火阈值存在一定局限性。

本研究建立了Steven试验数值计算模型，采用热力耦合模型和Arrhenius方程描述炸药的热反应，对低强度冲击下炸药受力和加热过程进行数值模拟，通过计算炸药温度，分析低冲击作用下炸药的点火规律。

1 数值计算

1.1 几何模型

在Steven试验中，炸药受到低速弹头撞击后，主要发生两种响应：一是当弹头速度超过一定的阈值速度以后，炸药在弹头撞击下受到冲击作用，内部温度逐渐升高，当炸药内部温度达到点火温度以后，炸药会点火燃烧；二是当弹头速度低于阈值速度时，炸药没有点火只是发生变形。因此，如何计算炸药受到冲击后的内部温度从而判断炸药点火情况是研究的重点。

根据文献［3］中的试验装置，采用LS-DYNA 程序中的二维轴对称计算功能，建立了Steven试验计算模型，对两种不同形状弹头（圆头弹头和小圆头弹头）撞击HMX 基炸药过程进行数值模拟［7］。为减少计算量，不考虑螺栓等部件。图1是圆头和小圆头两种弹头Steven试验的计算几何模型。圆头弹头部直径为60mm，小圆头弹头部的直径为30mm。两种弹头总质量均为1.2kg。

图1 圆头弹头和小圆头弹头Steven试验计算模型Fig.1 Calculated model of Steven impact test with different kinds of projectile head

1.2 基本方程

采用塑性动力学材料模型，其应力应变关系为［7］：

在加载段应力σ与应变ε保持线性，当应力大于屈服应力σs时，材料进入塑性，此后如果继续加载，应力应变关系仍然为线性，但是斜率发生变化，卸载曲线与加载段曲线斜率相同，当完全卸载后，材料中将保留塑性变形εp。

在一维条件下，如果结构的应力达到屈服应力，材料进入塑性阶段；在三维条件下，判断材料是否进入塑性使用VMISE屈服准则，即：

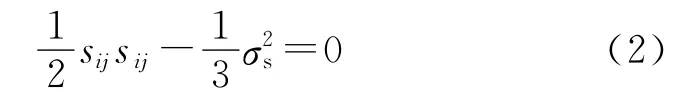
式中：sij=σij-1／3（σ11+σ22+σ33）δij为斜应力张量，当等效应力等于屈服应力时，材料开始进入塑性变形。

选用各向同性热材料模型描述炸药受力后的热作用，同时，计算炸药内部应力和温度变化，实现热和力的耦合计算分析。根据能量守恒原理，热问题的基本有限元方程可由热平衡方程推导求得［8］：

式中：［C］为比热矩阵，考虑系统内能的增加；［KT］为热传导矩阵，包括导热系数、对流系数及辐射率和形状系数；｛T｝为节点温度向量为温度对时间的导数；｛Q｝为节点热流率向量。

热力耦合计算的基本方程为［9］：

式中：｛u｝为节点位移向量；为节点速度向量；｛F｝为力向量，包括施加的节点力和由热应变引起的力。

除了炸药受力会引起温度升高外，炸药自热反应也是温度升高的主要因素。采用Arrhenius方程描述炸药自热反应［10］：

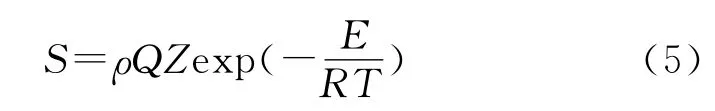
式中：S为源项；ρ为炸药密度；Q为反应热；Z为指前因子；E为活化能；R为普适气体常数；T为温度。整个模型的初始温度设为298K。表1给出了计算中HMX 基炸药的主要物化参数。

表1 HMX 基炸药的物化参数Table 1 Physicochemical parameters for HMX based explosive

2 计算结果及分析

2.1 圆头弹头Steven试验中炸药内部温度分析

弹头速度为55m／s，圆头弹头Steven试验中炸药内部不同时刻的温度分布见图2。

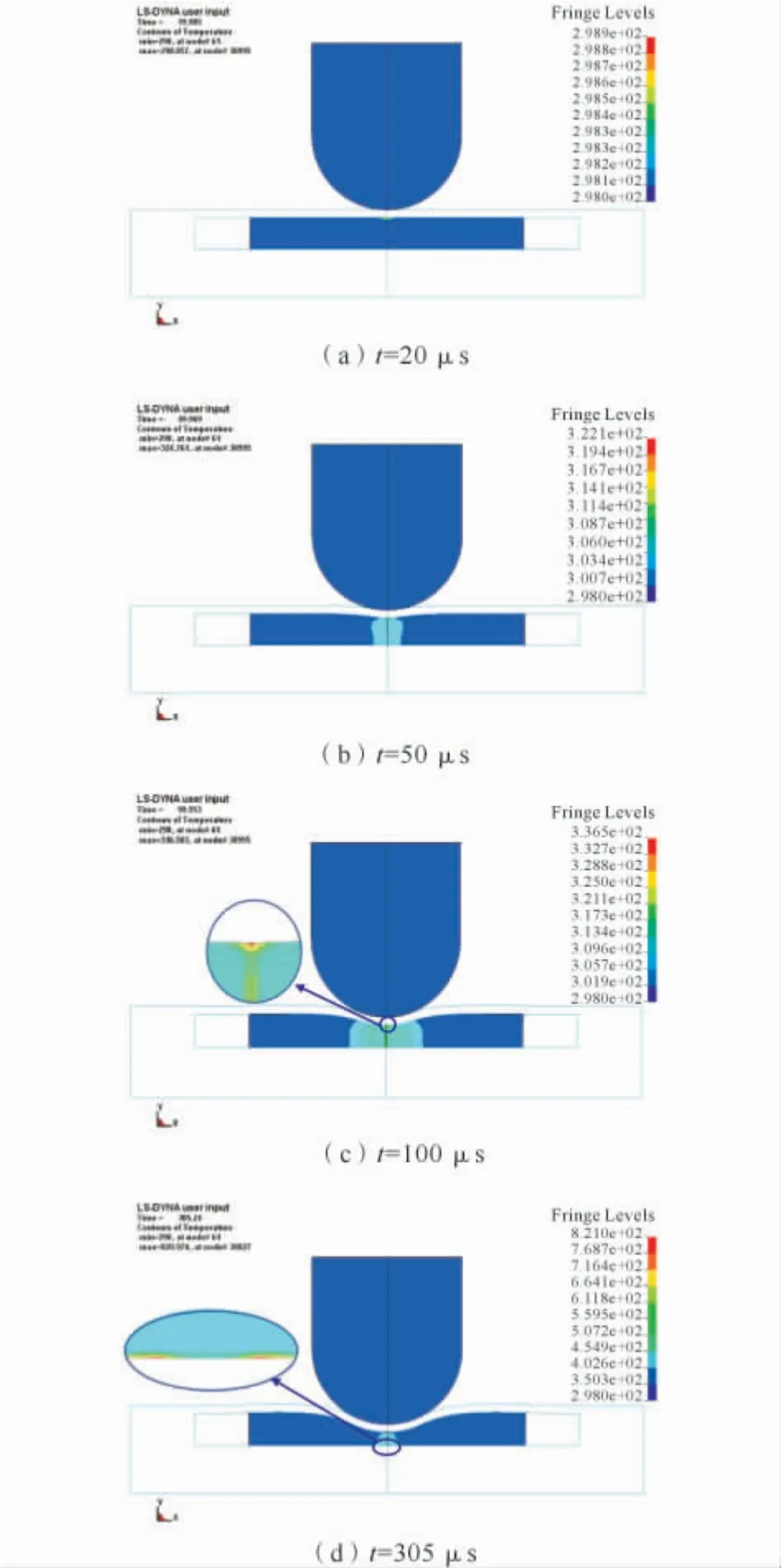
图2 弹头速度为55m／s时不同时刻炸药内部温度的分布Fig.2 Temperature distribution at different times of blunt projectile head with 55m／s head velocity

图2显示，20μs时，炸药试样受到弹头的撞击作用，上表面温度首先升高；随着弹头的不断作用，炸药内部高温区温度首先位于炸药试样上表面的中心点，约180μs时，炸药底部温度升高，并形成高温点，305μs时，炸药底部温度迅速上升，在距离底部中心2.5mm 处，温度达到最高，并超过炸药点火温度，炸药发生点火。

圆弹头以不同速度进行撞击时，炸药最高温点的温度-时间曲线见图3。由图3看出，当弹头速度低于50m／s时，炸药受力后温度升高，当达到一定温度后便不再升高，说明在此速度下炸药不会发生点火。在弹头速度为53m／s时，炸药受力后温度上升，达到一定温度后继续减慢上升，出现温度平台，但随后温度出现突跃上升，超过炸药点火温度，显示炸药发生点火，并且点火时间出现一定的延迟。随着弹头速度的增大，温度平台变小，点火延迟时间缩短。在当弹头速度接近60m／s时，炸药温度上升后，已没有温度平台，温度很快超过点火温度，炸药被快速点燃。

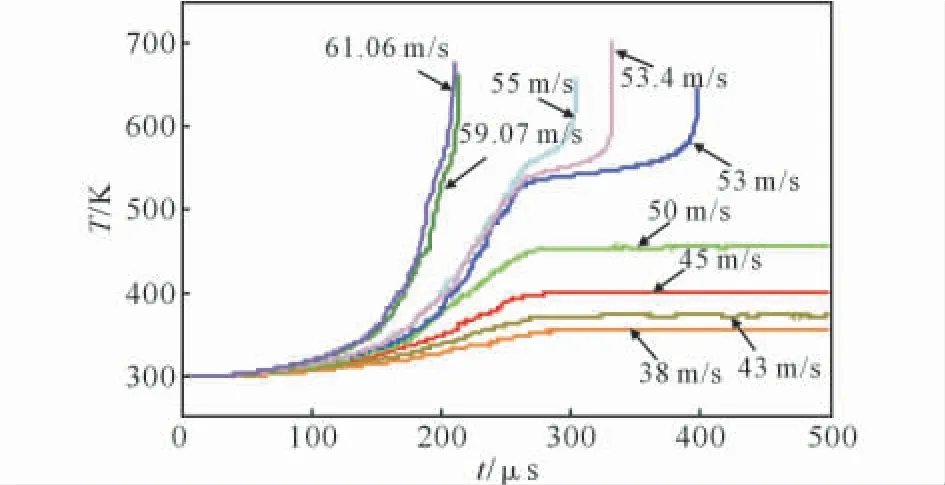
图3 圆头弹头Steven试验中炸药内部最高温度点的温度-时间曲线Fig.3 Temperature histories of the highest point in explosives of blunt projectile head with different velocities

表2给出不同速度圆头弹撞击炸药时，炸药反应的计算结果，并与文献值［3］进行了对比。计算结果表明，对于圆头弹，当弹头速度高于53.4m／s时，炸药发生点火反应，当弹头速度低于43m／s时，炸药没有发生反应。该结果与文献值一致。

2.2 小圆头弹头Steven试验中炸药内部温度分析

弹头速度为70m／s时，小圆头弹撞击下炸药内部温度的分布见图4。图4 结果表明，炸药受到撞击后，首先也是上表面中心处温度升高，随着弹头的不断作用，高温区主要集中在炸药中轴线上，并在中轴线靠上的部分出现最高温度点。

表2 不同速度圆头弹头撞击下炸药反应计算结果与试验结果Table 2 Simulated results and test ones with blunt projectile head

图4 70m／s速度下小圆头弹炸药试样不同时刻的内部温度分布Fig.4 Temperature distribution at different times of little blunt projectile head with 70m／s head velocity

小圆头弹以不同速度撞击时，炸药最高温度点的温度-时间曲线见图5。从图5可以看出，当弹头速度超过68m／s时，炸药内部温度出现跃升，超过炸药的点火点；当速度为65m／s时，温度升至527K 后趋于平稳，说明此速度下炸药不会发生点火。与圆头弹相比，小圆头弹作用时达到点火阈值所需弹头速度提高，炸药的点火延迟时间缩短。

2.3 弹头形状对内部压力的影响分析

在炸药内取2个特征点，观察炸药受力后的压力变化情况。1 号点位于炸药上表面中心，2 号点位于炸药下表面中心，如图6 所示。弹头速度为60m／s时，圆头和小圆头弹头在2个特征点的压力-时间曲线见图7。从图7可以看出，在炸药上表面中心，圆头弹和小圆头弹对炸药的初始撞击压力基本一致，但在后期小圆头弹对炸药作用压力高于圆头弹头；而在炸药下表面中心，圆头弹头作用下的炸药压力高于小圆头弹头。在小圆头弹作用下，炸药上表面压力明显高于下表面；而对于圆头弹，炸药下表面最大压力高于上表面。可见，弹头形状对炸药受力过程有较大影响，使炸药点火阈值和点火点位置产生差别。在圆头弹作用下，炸药在底部发生点火，而小圆头弹是在靠近炸药上部发生点火。

图5 小圆头弹头Steven实验中炸药最高温度点的温度-时间曲线Fig.5 Temperature histories of the highest point in explosives of little blunt projectile head with different head velocities

图6 所取特征点位置Fig.6 Position of characteristic points

图7 弹头速度为60m／s时两个特征点的压力-时间曲线Fig.7 Pressure histories of characteristic points with head velocity of 60m／s

3 结 论

（1）建立了炸药Steven试验数值计算模型，采用热力耦合模型和Arrhenius方程描述炸药的热反应，计算炸药点火的弹头阈值速度与文献值相符，表明计算模型能够分析低强度冲击下炸药的响应状态。

（2）Steven试验中，当弹头速度为阈值速度时，炸药点火存在一定的延迟时间，随着弹头速度的增大，延迟时间缩短。

（3）弹头形状对炸药受力过程有较大影响。在圆头弹作用下炸药在底部发生点火，而小圆头弹作用下在炸药上部发生点火。

［1］章冠人，陈大年.凝聚炸药起爆动力学［M］.北京：国防工业出版社，1991.

［2］Chidester S K，Green L G，Lee C G.A frictional work predictive method for the initiation of solid high explosives from low pressure impacts［C］／／10th International Detonation Symposium.Boston：Boston Office of Naval Research，1993：785-792.

［3］Chidester S K，Tarver C M，Low amplitude impact testing and analysis of pristine and aged high explosives［C］／／11th Symposium（International）on Detonation CO.Aspen：Office of Naval Research，1998：93-100.

［4］Switzer L L.Threshold studies of heated HMX-based energetic material targets using the steven impact test［J］.Shock Compression of Condensed Matter-2003，2003：1045-1048.

［5］韩勇，向永，韩敦信，等.Steven 试验中模拟材料D-90031力学响应的数值模拟［J］.含能材料，2004，12（z2）：545-547.

HAN Yong，XIANG Yong，HAN Dun-xin，et al.The numerical modeling of dynamical response of S.L.D-90031in STEVEN test［J］.Energetic Materials，2004，12（22）：545-547.

［6］代晓淦，文玉史，李敬明，等.Steven含TNT 类炸药的响应特征［J］.火炸药学报，2011，34（3）：48-51.

DAI Xiao-gan，WEN Yu-shi，LI Jing-ming.Reaction characteristics for explosive containing TNT in Steven test［J］.Chinese Journal of Explosives and Propellants，2011，34（3）：45-51.

［7］Lawrence livermore national laboratory.LS-DYNA Μser′s Manual［M］.California：University of California，2001.

［8］陶文栓，李永堂.热工程学［M］.武汉：武汉理工大学出版社，2001.

［9］HU Zhong，ZHU Li-Hua，WANG Bei-yi，et al.Computer simulation of the deep extrusion of a thin-walled cup using the thermo-mechanically coupled elasto-platic FEM［J］.Journal of Materials Processing Technology，2000，102（1）：128-137.

［10］McCelland M C，Maisenschein J L，Howard W M，et al.ALE3Dsimulation of heating and violence in a Fast Cookoff experiment with LX-10［C］／／13th International Detonation Symposium.Norfolk：Office of Naval Research，2006.