在污染环境中捕食-食饵模型的生存分析

赵堃

(东北大学信息科学与工程学院，辽宁沈阳110819)

自1926年Volterra提出著名的Lotka-Volterra微分方程模型以来，该模型已经引起了众多生物学家、数学家极大的兴趣，并得到了许多较好的结论［1－4］.两种群相互作用的微分方程模型 ˙x1=x1F1(x1，x2)，˙x2=x2F2(x1，x2)描述了2个种群之间的捕食与被捕食作用、相互竞争作用以及互惠作用.许多生态数学的问题都可以归结为该模型.鉴于该模型的实际生态意义，引起了许多学者的关注.工农业的快速发展，给当今社会带来了莫大的好处，同时也给生态系统造成直接或间接的破坏影响，因此，研究污染环境中种群生存与绝灭在理论上显得越来越重要.1984年Hallam T G等人利用数学模型定性研究毒素对生物种群生存的影响，为这一研究方向揭开了序幕，其在文献［1］中提出的平均持续生存的概念和积分均值法，为这方面的研究奠定了基础.近年来，许多学者对大容量的污染环境中单种群、两种群及三种群模型的生存与绝灭的阈值进行了研究，并取得了较好的结果［5－9］.本文在此基础上研究污染环境中两种群相互作用的微分方程模型，得到种群持续生存与绝灭的阈值，且推广了文献［1］中的结果.为实际应用提供了一定的理论依据.

1 模型及假设

为书写简洁，引入记号:

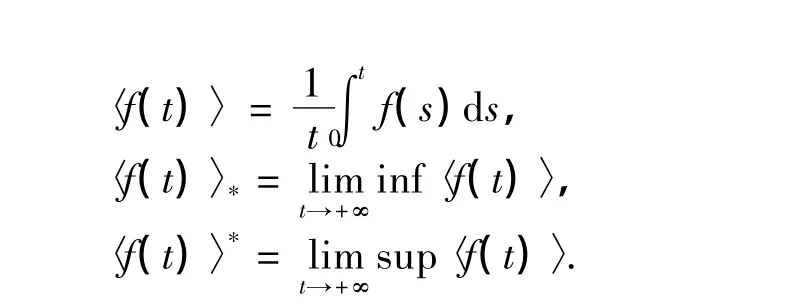
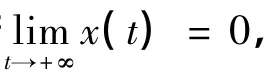
如果用xi(t)(i=1，2)、CE(t)、C0(t)分别表示t时刻2个种群的数量、环境中有害物质的浓度、种群体内毒素的浓度，则xi(t)(i=1，2)为有界函数.取

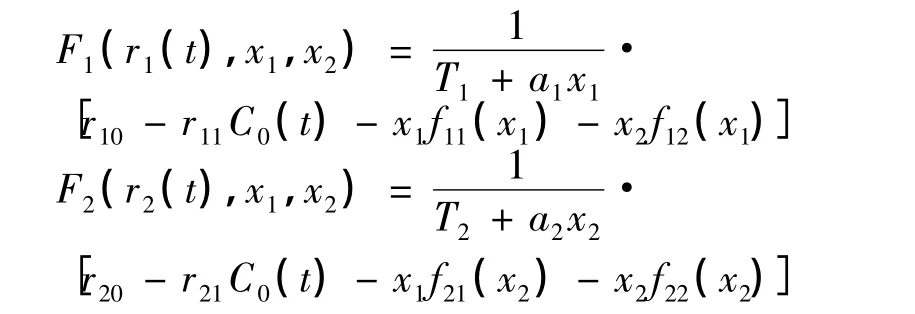
建立如下污染环境中捕食-食饵种群模型:

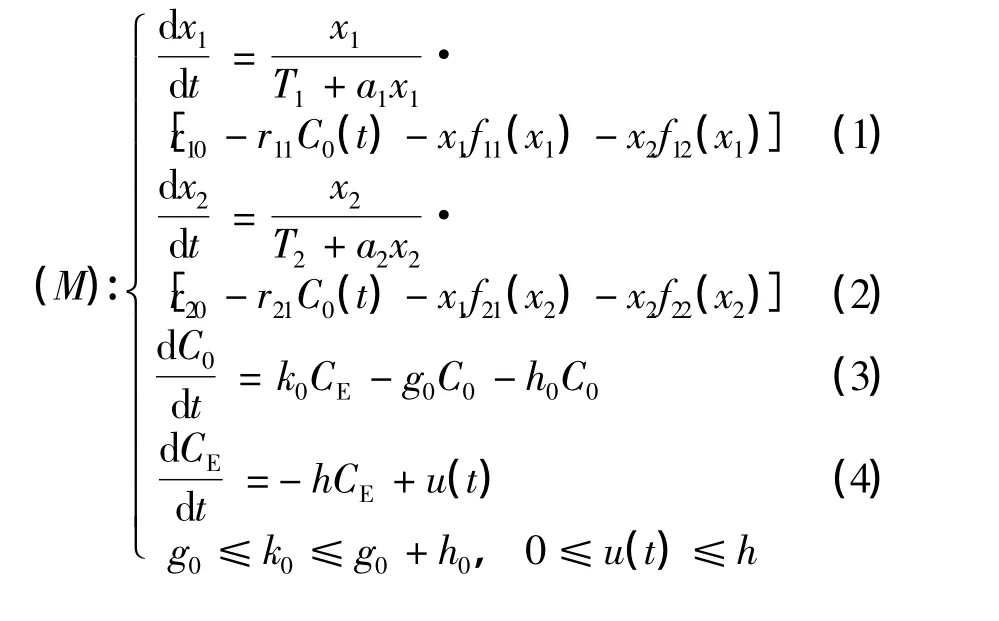
初始条件为xi0=xi(0) ＞0(i=1，2)，C0(0)≥0，CE(0)≥0.其中，ri0、ri1分别表示第i个种群的自然增长率和对毒素剂量的反映系数，连续有界量u(t)是外界向环境输入的输入率，且Ti＞0，ai≥0(i=1，2)，r10＞0，r20＜0，r11＞0，r21＞0，fij(xi)(i，j=1，2)均为连续函数，且mij＜fij(xi)＜Mij，M21＜0，mij＞0(i≠2，j≠1).详情见文献［1］.

记:Δ1=M11r20-M21r10，

Δ=M11M22-M12M21

显然Δ＞0，~Δ1＞0.

由于从模型(M)中(3)式和(4)式可以解出C0(t)=g(u(t))，因此，寻找对u(t)的控制阈值可转化成通过模型(1)式和(2)式寻找对C0(t)的控制阈值.

2 定理及证明

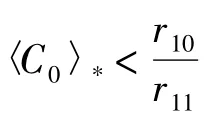
证明:由(1)式有:

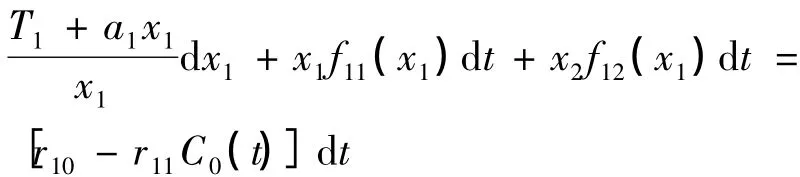
两端积分并除以t得:

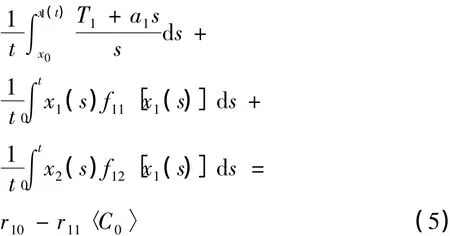
由于

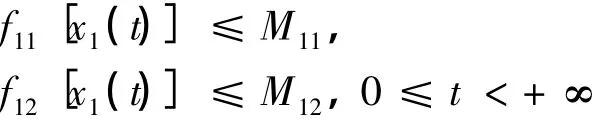
如果〈x1〉*=〈x2〉*=0，有

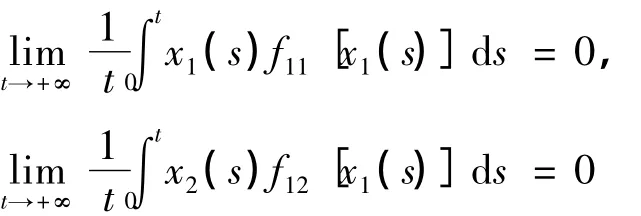
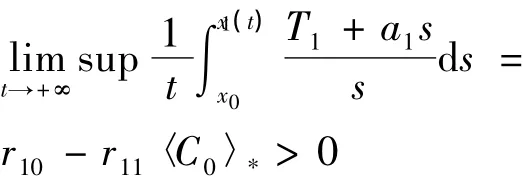
(2)由(1)式和(2)式有:

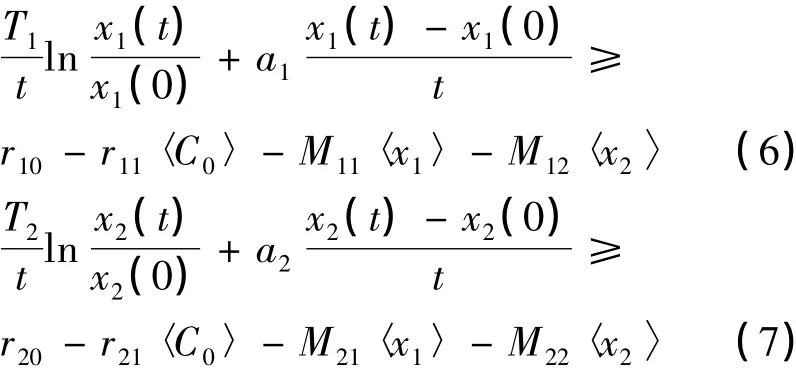
将(6)式和(7)式分别乘以-M21和M11相加得:

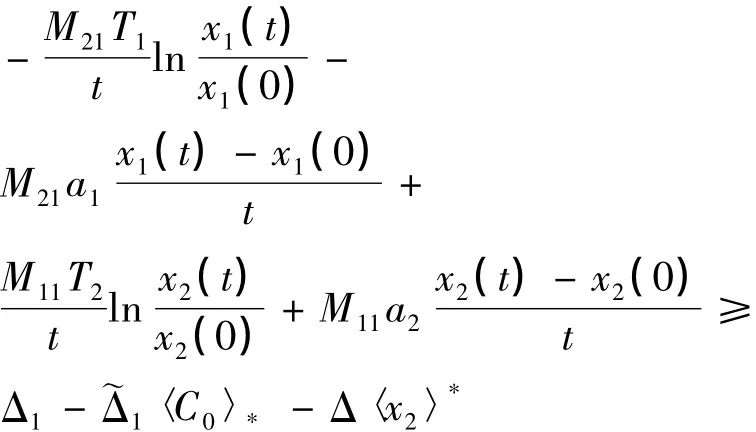
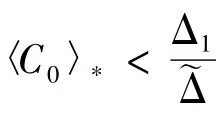
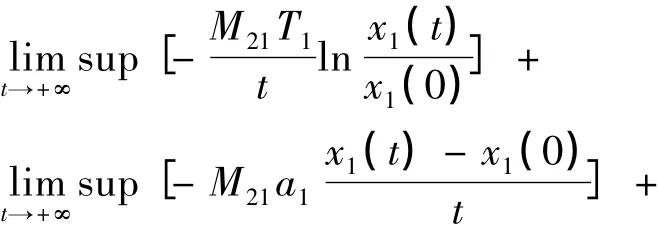
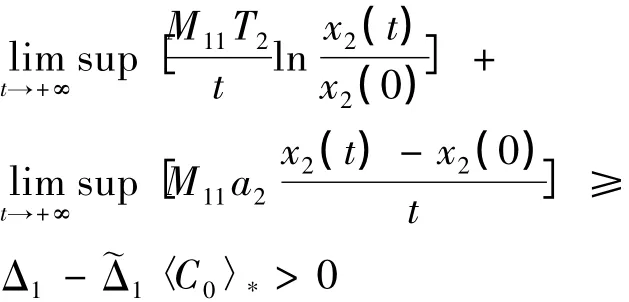
此式不可能成立，因为x1(t)与x2(t)均有界，所以必有〈x2〉*＞0.又 x1(t)的抗毒能力强于x2(t)，所以〈x1〉*＞0，即两种群均弱平均持续生存.

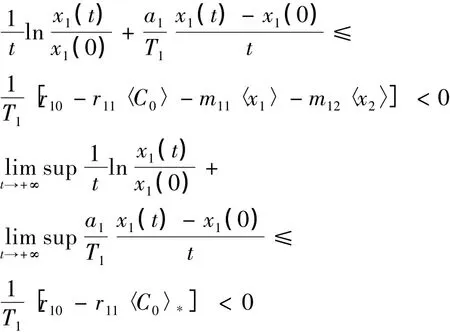
即两种群均走向绝灭.

3 结论

在模型(M)中，当fij(xi)=aij(aii＞0，i=1，2，a12＞0，a21＜0)为常数，Ti=1(i=1，2)，ai=0时，则(1)和(2)式变为:

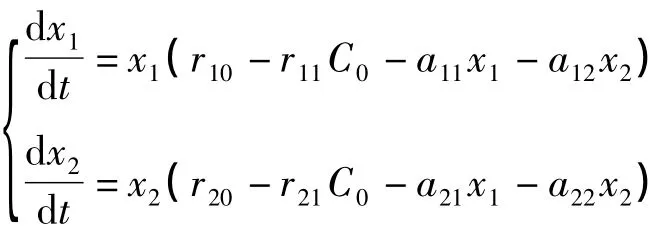
则得到与文献［1］中相同的结论，因此，本文推广了文献［1］中的结果.

［1］ 马知恩.种群生态学的数学建模与研究［M］.安徽:安徽教育出版社，1996:168－199.

［2］ 刘玉琏，傅沛仁.数学分析讲义［M］.北京:高等教育出版社，1992:126－130.

［3］ 马知恩，周义仓.常微分方程定性与稳定性方法［M］.北京:科学出版社，2001:204－235.

［4］ 阎慧臻，马知恩，刘燕.二维Lotka-Volterra竞争系统的β持续生存与 β绝灭［J］.生物数学学报，2010，25(2):294－298.

［5］ 祁延超，刘兵，张丽霞.一类污染环境中非自治捕食-食饵系统的持续生存与灭绝［J］.生物数学学报，2011，26(3):294－298.

［6］ 冯由玲，王克，孙静懿.具污染与捕获的Logistic单种群的持续生存及绝灭［J］.生物数学学报，2006，21(3):365－369.

［7］ 李长生.污染环境中两种群的生存阈值［J］.潍坊学院学报，2004，4(2):1－2.

［8］ 靳祯.污染环境三维Volterra竞争系统生存与绝灭的阈值［J］.华北工学院学报，1996，13(2):201－208.

［9］ 董雨滋，王拉娣.污染环境中三维竞争系统的生存阈值［J］.系统科学与数学，1997，17(3):221－225.