基于电热模型的IGBT结温预测与失效分析

汪波，胡安，唐勇

(海军工程大学 舰船综合电力技术国防科技重点实验室，湖北 武汉430033)

0 引言

绝缘栅双极晶体管(insulated gate bipolar transistor，IGBT)是一种综合了场效应晶体管(metal oxide semiconductor field effect transistor，MOSFET)和双极型晶体管(bipolar junction transistor，BJT)结构的复合器件，同时吸收了二者的优点[1－2]。在大容量高性能电力电子装置中，考虑到高功率密度的要求，需要将IGBT参数应用到极限状态，这会带来较高的工作结温，而结温受多种因素的限制。首先，IGBT内部硅芯片材料的熔点温度大约为1 340℃;其次，基区低掺杂浓度的PN结在本征温度时，材料会表现出本征半导体的特性;再次，IGBT结温受外部散热能力的限制，当产生的热量不能全部被散走时就会引发热电正反馈，导致结温不控上升，最终发生失效;最后，IGBT结温受内部封装技术的限制，主要是芯片正面的键合线、芯片背面的焊接和直接覆铜层(direct bonding copper，DBC)至基板的焊接。

IGBT结温测量通常采用红外测温法、电敏感参数法和热偶法[3－6]。红外测温法测量的是模块内部硅芯片表面温度分布，需要打开封装并去除硅胶，会损坏器件的完整性，而且硅芯片表面覆盖一层铝合金，很难测量到内部PN结的实际温度。电敏感参数法测量的是硅芯片平均温度，通常将小电流时的饱和压降和栅极门槛电压作为热敏参数，测量时需要进行电路切换。热偶法测量的是硅芯片表面某一点的温度，同样需要打开封装。因此，3种结温测量法各有优缺点，通常应用于实验室研究测试，而在实际工程应用中很难实施。由于结温对IGBT的安全应用、寿命与可靠性评估具有决定性的影响且很难测量，因此无损预测结温具有重要的理论和工程意义。

本文提出一种基于电热模型的IGBT结温预测方法。首先建立IGBT通态压降模型，考虑到器件内部参数和材料半导体物理常数与温度的关系，建立IGBT功耗与温度的电热模型，然后在分析IGBT热平衡基础上得到稳态时的结－壳传热方程，联立电热模型和传热方程求解得到热平衡时的结温，通过仿真及实验来验证所提方法的正确性。最后对由结温过高引起的失效进行分析，表明焊料出现空洞、熔化以及键合线剥离、断裂是易发生失效的部位。

1 电热模型

1.1 通态压降模型

IGBT本质上是一个由MOSFET驱动的BJT管，在结构上与功率MOSFET相似。IGBT根据电场是否穿通基区分为穿通(PT)型和非穿通(NPT)型，其结构差异在于PT型加入了一个重掺杂的缓冲层。图1中虚线框内为穿通(PT)型或场终止(FS)型IGBT的一个元胞结构，NPT型只需去掉图中的N+缓冲层/场终止层。

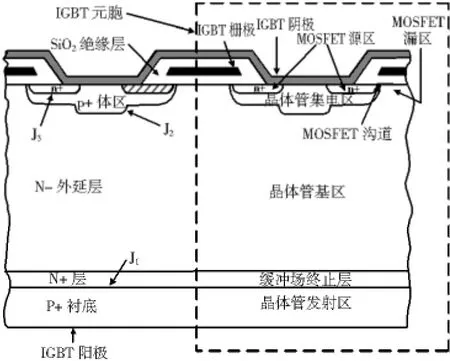
图1 PT或FS型IGBT元胞结构Fig.1 Structure of PT or FS IGBT cell

由IGBT结构可知，NPT型压降由内部MOSFET沟道电压、准中性基区压降以及P+发射极/N－基区结压降3部分组成[7]。PT型同样也由这3部分组成，只是N+缓冲层/N－基区结压降构成了总的压降，由于缓冲层内本身掺杂浓度很高，过剩电子的注入引起电子浓度变化很小，电子费米能势几乎没有发生变化，因此缓冲层内的电压降可以忽略不计。

通态压降模型建立的基本途径是根据一定的假设和边界条件求解载流子的连续性方程，得到过剩载流子的浓度分布，将其带入电流输运方程求得空穴电流和电子电流的表达式，再推出压降的表达式[8]。PT型通态模型分析坐标系如图2所示，其中x轴为基区坐标系，x*为缓冲层坐标系。

图2 PT型模型分析坐标系Fig.2 Coordinate systems of PT model

内部MOSFET工作在线性电阻区，沟道压降Vch可表示为

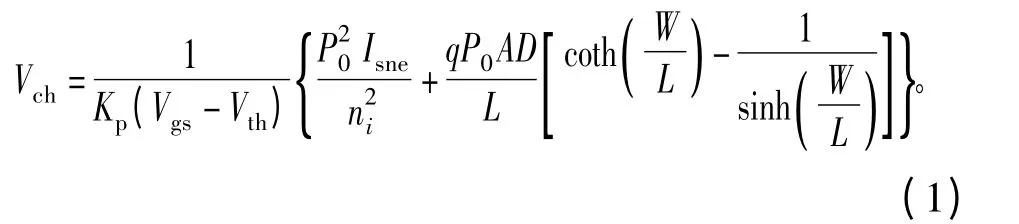
式中:Kp为内部MOSFET跨导;Vgs为栅极驱动电压;Vth为栅极门槛电压;Isne为发射极反向电子饱和电流;ni为本征载流子浓度;q为电子电荷量;A为芯片有效工作面积;D为基区双极扩散系数为基区双极扩散长度，τ为基区内过剩载流子寿命;W为准中性基区宽度;P0为 x=0处的过剩空穴浓度。

准中性基区压降Vqnb可由电子准费米电势梯度积分得到，即

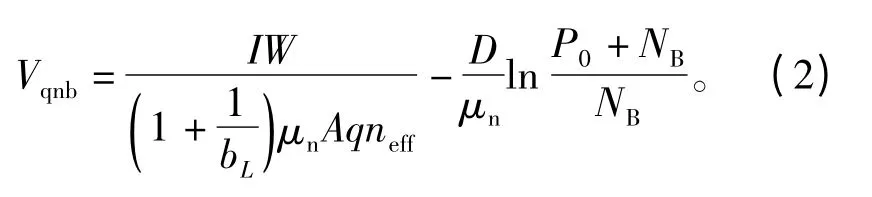
式中:I为总的导通电流;bL为基区双极迁移率;μn为基区电子迁移率;NB为基区掺杂浓度;neff为准中性基区有效电子浓度，其表达式为

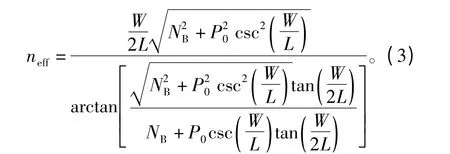
N+缓冲层/N－基区结的电压降VPN为

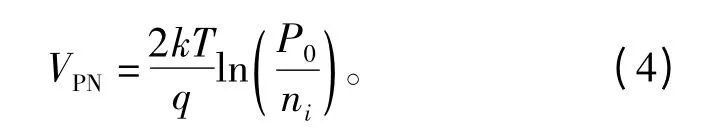
式中:k为玻尔兹曼常数;T为绝对温度。

从上述关系式中可以看出，只需求解过剩空穴浓度P0就可以得出总的压降。设定边界条件δP(x*=0)=PH0和 δP(x*=WH)=PHW，WH为缓冲层宽度，根据N+缓冲层和N－基区边界处空穴电流相等，可得到x*=0处的过剩空穴浓度PH0，根据N+缓冲层和N－基区边界处的准热平衡近似可得x*=WH处的浓度PHW，通过求解缓冲层内的空穴电流和电子电流可得总的电流表达式，联立方程求解得到x=0处的过剩空穴浓度P0，即

式中:DpH为缓冲层内空穴扩散系数为缓冲层内的扩散长度，τH为缓冲层内的载流子寿命;WH为缓冲层厚度;NH为缓冲层内的掺杂浓度。

对于NPT型，P+发射极/N－基区结处，即x=0处的过剩空穴浓度为

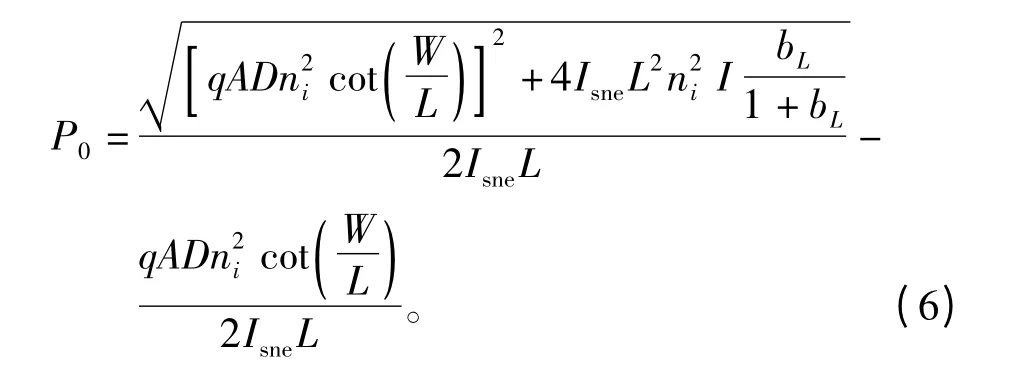
因此，IGBT总的压降可表示为

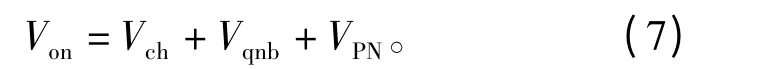
1.2 通态功耗的电热模型

功率半导体器件 IGBT对温度极为敏感，从建立的通态压降模型来看，与温度相关的参数分为两类。第一类是器件的内部参数，包括过剩载流子寿命、栅极门槛电压、跨导和发射极电子饱和电流，采用经验公式进行近似处理，即

式中:τ(T0)、Vth(T0)、Kp(T0)和 Isne(T0)分别为过剩载流子浓度、门槛电压、跨导以及发射极电子饱和电流参数在常温 T0时的值;τ(Tj)、Vth(Tj)、Kp(Tj)和Isne(Tj)为温度Tj时的值;K为门槛电压的系数，可以测量提取得到。

另一类是材料的半导体物理常数，包括本征载流子浓度、载流子迁移率和扩散系数。本征载流子浓度随温度的变化关系为

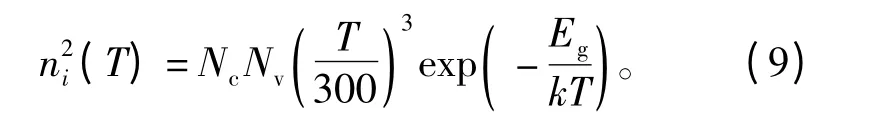
式中:Nc=2.8×1019cm－3为导带有效状态密度;Nv=1.04×1019cm－3为价带有效状态密度;Eg为硅材料的禁带宽度，与温度呈线性关系，即

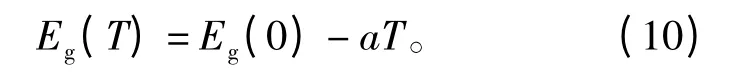
式中:Eg(0)=1.20 6 eV为绝对零度时的禁带宽度;a=2.732 5×10－4eV/K为比例系数。将式(10)代入式(9)可得

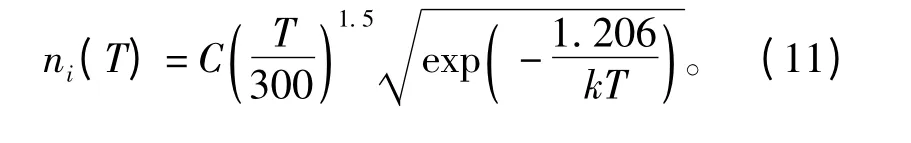
式中:C=8.324 ×1019cm－3·K－1.5为比例系数。

载流子的迁移率反映了载流子的平均漂移速度与电场之间的关系，对准中性基区压降的影响大。载流子迁移率与温度和掺杂浓度有关，随温度升高而减小，随掺杂浓度增大而减小，由于难以用数学模型来准确表述与温度和掺杂浓度的关系，因此仿真时，分别在基区掺杂浓度和缓冲层掺杂浓度水平上选取多个温度点，通过查表得到载流子迁移率，代入计算得到压降在多个温度点的值，再拟合成一条曲线。对于实验所选IGBT器件，内部参数提取基区掺杂浓度和缓冲层掺杂浓度分别为1014cm－3和1017cm－3数量级时，查找多个温度点的迁移率并将其拟合成如图3所示的曲线，其中，μn和μp分别为基区电子和空穴迁移率，μn1和 μp1分别为缓冲层电子和空穴迁移率。

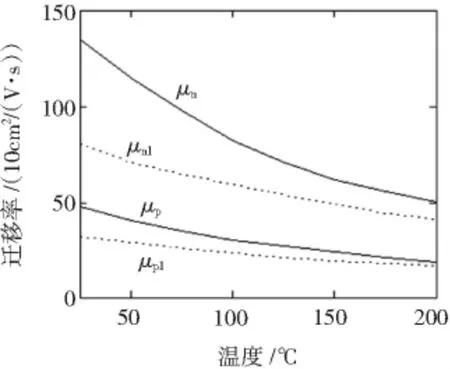
图3 不同掺杂浓度时的迁移率Fig.3 Mobility under different doping concentration

载流子的扩散系数与迁移率相关，二者之间满足爱因斯坦关系，即

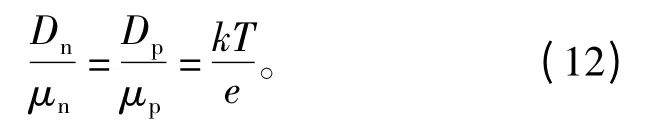
式中:Dn为电子扩散系数;Dp为空穴扩散系数;e为电子电荷量。

通过提取IGBT内部参数，主要是基区掺杂浓度、缓冲层掺杂浓度、基区宽度、缓冲层宽度、芯片有效工作面积、基区内过剩载流子寿命、缓冲层过剩载流子寿命、内部MOSFET跨导和发射极电子饱和电流，其中前5项是与温度无关的量，后4项与温度相关，文献[9－10]给出了这些内部参数的具体提取方法，得到IGBT压降随温度的关系，也就得到了通态功耗的电热模型，即

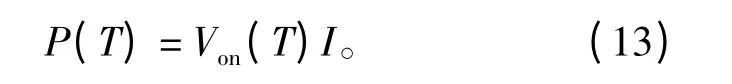
2 IGBT热平衡分析

IGBT工作时产生的热量通过DBC层传递到铜底板，底板再向散热装置传递热量，当散走的热量与硅芯片产生的热量相等时，系统到达热平衡状态，各部分温度保持稳定。对于一个由IGBT器件、散热装置和冷却介质(水冷、强迫风冷)构成的确定组合，其稳态功耗表示为

式中:Tj为结温;TA为环境温度;RthJA为结－环境热阻;TC为壳温;RthJC为结 －壳热阻;P为 IGBT的功耗。

式(14)将器件的功耗与环境温度和冷却方法(用热阻 RthJA表示)联系起来，但是适用的情况是IGBT系统已进入热平衡状态，各部分建立起稳态的温度分布。如果功率耗散发生变化的时间小于建立稳态所需的时间，即还没到达热平衡状态时，热容就会影响到热量的传导，此时必须用瞬态热阻抗来描述结温的变化。结－环境瞬态热阻抗定义为

结－壳瞬态热阻抗定义为

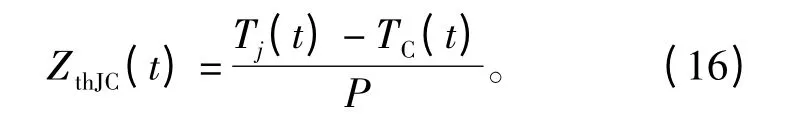
由于瞬态热阻抗总是小于稳态热阻抗，而且瞬态热阻抗随着时间的变化逐渐逼近稳态热阻抗，因此瞬时结温和壳温也总是小于稳态时的结温和壳温，随着时间的变化逐渐逼近稳态时的值。当到达热平衡状态后，热阻保持恒定，即可联立式(13)和式(14)求解稳态时的结温。由于结－环境热阻由结－壳热阻和壳－环境热阻两部分组成，其中结－壳热阻可以测量且基本保持不变，而壳－环境热阻随外界变化的不确定性因素很多，与散热装置的接触面积、冷却介质有关，还会随环境而变化，因而较难准确得到，这就给方程式求解带来不便。而式(14)中IGBT结 －壳热阻可准确提取，仅考虑一维向下热传导，测量壳温时将热电偶布置在芯片垂直正下方，使测得的壳温最高，结温测量采用电敏感参数法，所有测试仪器用Labview软件控制，文献[11－12]给出了热阻的提取方法。

联立IGBT功耗的电热模型式(13)和结－壳传热方程式(14)，可以求解热平衡时的结温，其方法采用图解法，二者的交点即为稳态时的结温。

3 实验研究及失效分析

3.1 实验研究

对建立的IGBT压降与温度关系的电热模型进行实验验证。所选 IGBT型号为GD50HFL120C1S，其额定电压和直流电流分别为1 200 V和50 A，采用ABB公司制造的芯片，封装在国内完成，这是一种具有缓冲层结构的PT型器件。

将IGBT模块固定在带加热电阻丝的底板上，电流由安捷伦6 680 A电流源提供，通过控制底板加热来改变温度。结温测量采用电敏感参数法，电参数选取小电流时的饱和压降，采用安捷伦6 643 A电流源提供0.1 A的小电流，先定标得到小电流时导通压降与温度的关系，即

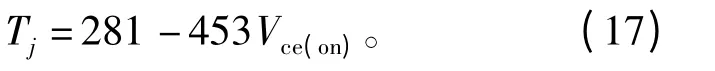
式中，Vce(on)为饱和压降。

完成温度标定后，再将小电流时的导通压降换算成结温。IGBT导通压降的温度特性测试电路如图4所示，其中I为加热大电流源，i为测试结温的小电流源。

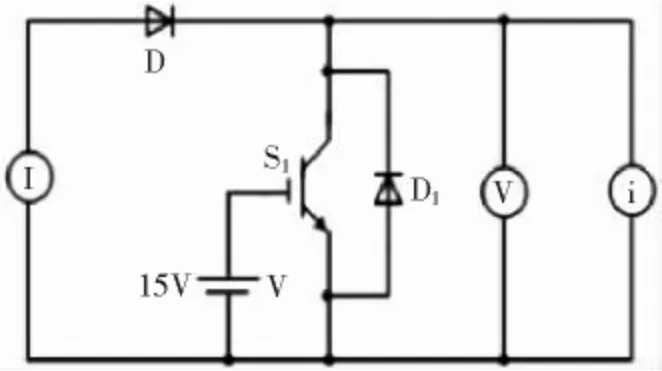
图4 IGBT导通压降测试电路Fig.4 Test circuit of on－state voltage

图4 中，首先导通大电流源给芯片加热，小电流源也持续导通，但与大电流源相比可以忽略不计，同时采用电压表和热电偶测量导通压降和底板壳温。经过一段时间，壳温上升到最大值后，系统到达热平衡状态，此时切断大电流源，仅由小电流源供电，测量切换后的导通压降换算成结温。实验中，由于IGBT芯片热容很小，结温随电流源切换变化很快，采用普通的电压表测量压降会带来较大的误差，因此采用高速LeCroy wavepro7000示波器测量电流源切换瞬间压降，其变化波形如图5所示。

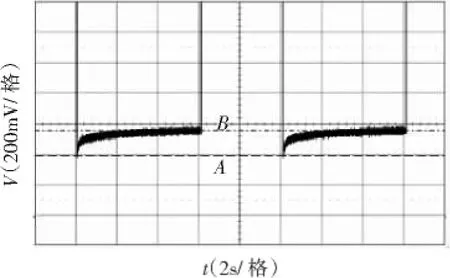
图5 电流切换瞬间电压波形Fig.5 Voltage waveforms in current switching

从图5中可以看出，在电流源切换瞬间，导通压降有个尖峰，从最小值上升到最大值要经过大约2 s，采用普通电压表测量得到的是稳态压降，即曲线B对应的压降，此时IGBT结温已经有大幅度的下降，而采用示波器测量得到的压降即曲线A，可接近实际结温。

在电流分别为50 A和70 A时，测量不同温度下的饱和导通压降，以及采用IGBT电热模型仿真得到的压降如图6所示。

图6 通态压降随温度的关系Fig.6 Relation of on-state voltage with temperature

从图6中可以看出，在电流为50 A时，压降随温度的变化率约为0.002 2 V/℃;电流为70 A时，压降随温度的变化率约为0.003 3 V/℃。压降随着温度的上升小幅增加，且随着电流的增大，变化率也会增大。因此，仿真值与实测值基本吻合，同时也验证了通态功耗电热模型的正确性，存在的误差是由内部参数提取的精确度以及半导体物理常数与温度关系的误差造成的。

对热平衡时的结温预测进行实验，选用相同型号IGBT模块，结 －壳稳态热阻提取为0.32 K/W。在电流为50 A时，到达热平衡态时测得壳温T1为55℃，采用基于电热模型的结温预测法的仿真结果如图7所示，曲线 AC表示IGBT通态功耗电热模型，曲线AB表示结－壳传热功耗，二者的交点A表示到达热平衡时的结温，大约为85℃，关断大电流源瞬间测量小电流时的压降换算成结温为87℃，仿真值基本与实测值相吻合。减小散热底板的水流速度，曲线AB向右移动，到达热平衡时的壳温 T2=95℃时，结－壳传热曲线移动到 CD，二者的交点C为稳态结温点，仿真得到结温为128℃，切换电流后计算得到的结温为129℃，两者基本一致。当电流增大到70 A时，IGBT的功耗曲线为BD，壳温分别为55℃和95℃时，与结－壳传热曲线的交点B和D分别为107℃和153℃，与实际测量的结温值相吻合。

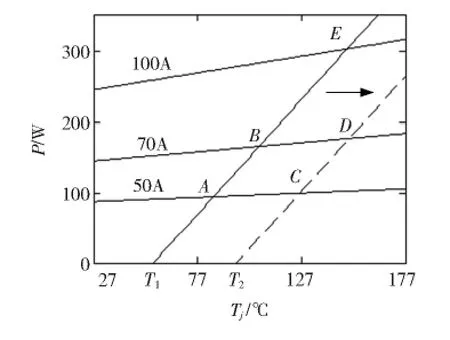
图7 热平衡曲线Fig.7 Curve of thermal equivalent

电力电子装置中IGBT器件通常工作在脉冲开关状态，其功耗由开关功耗、导通功耗和断态功耗3部分组成，IGBT功耗的温度特性表现在低温阶段近似线性上升，而在高温阶段成指数特征上升。因此，IGBT结温预测需要考虑IGBT开关瞬态模型和断态模型分别得到开关功耗和断态。同样，联立 IGBT电热模型和传热功耗方程，通过监测壳温也可实时预测结温。

3.2 失效分析

IGBT功耗增大或散热能力下降时，壳温上升使结－壳传热曲线向右移动，热平衡时的交点也同时向右移动，若这个交点超出了IGBT的结温安全应用范围，就会发生失效。由于硅芯片的本征温度点和熔点都要远超出手册给定的安全工作温度点，且通态功耗曲线随温度近乎线性增加，不会发生热奔，因此通态时结温过大的失效主要发生在键合引线和焊料层。而在脉冲工作模式下，由于集电极漏电流在高温阶段与结温成指数特征增加，一旦产生功率增量大于结－壳所能传导的热量增量时，进入热电正反馈，热奔引起硅芯片失效，因此失效主要发生在硅芯片，也可能发生在键合引线和焊料层，而通态时失效主要发生在键合引线和焊料层等封装工艺，。

对两种情况下由结温过高引起的失效进行实验，为方便观察失效部位，采用从厂家订购的打开封装且未覆盖硅胶的IGBT模块。第一，在电流为70 A时，通过减小散热装置的水流速度，结－壳传热曲线CD向右移动，交点对应的结温增大，且超出安全应用范围，经过一段时间后观察到IGBT电极根部的焊料开始出现熔化，如图8(a)所示。第二，在电流增大到100 A时，达到了额定电流的2倍，壳温和结温迅猛上升，采用大的水冷流速散热，壳温上升到95℃时，仿真表明热平衡时的交点超出了结温安全应用范围，达到190℃以上，经过大约10 min后发生了失效，观察到硅芯片表面连接键丝发生断裂，如图8(b)所示。重复上述实验，得到了相同的失效模式。

图8 IGBT结温过高的失效模式Fig.8 Failure mode under high junction temperature

4 结语

本文提出了一种基于IGBT电热模型的结温预测方法，通过监测热平衡时的壳温可以实时得到对应的结温，用于指导IGBT散热装置的设计以及电流的极限应用，同时为器件的寿命与可靠性评估提供重要的依据。该方法也可移植到脉冲工作模式下的结温预测中，功耗计算要考虑开关损耗和断态功耗。

IGBT通态时结温过高的失效分析结果表明，键合引线和焊料层等封装工艺是易发生失效的薄弱部位，通过改进内部封装工艺(比如采用更先进的焊料和键合引线以及优化内部连接)可以支持更高的结温。

[1]陈坚.电力电子学－电力电子变换和控制技术[M].北京:高等教育出版社，2004:45－46.

[2]吴郁，张万荣，刘兴明.功率半导体器件—理论及应用[M].北京:化学工业出版社，2005:269－280.

[3]HAMIDI A，COQUERY G，LALLENMAND R，et al.Temperature measurements and thermal modeling of high power IGBT multichip modules for reliability investigations in Traction Application[J].Microelectronics Reliability，1998，38(6 －8):1353 －1359.

[4]BAZZO J P，TIAGO L，MARCIO V，et al.Thermal characteristics analysis of an IGBT using a fiber bragg grating[J].Optics and Lasers in Engineering，2012，50(2):99 －103.

[5]BARLINI D，CIAPPA M，CASTELLAZZI A，et al.New technique for the measurement of the static and of the transient junction temperature in IGBT devices under operating conditions[J].Microelectronics Reliability，2006，46(9 －11):1772 －1777.

[6]MAHERA M，PAUL P A，JOHNSON C M，et al.Power electronic device temperature estimation and control in pulsed power and converter applications[J].Control Engineering Practice，2008，16(12):1438－1442.

[7]袁寿材.IGBT场效应半导体功率器件导论[M].北京:科学出版社，2008:70－74.

[8]唐勇.大容量特种高性能电力电子系统中器件模型理论研究[D].武汉:海军工程大学电气工程学院，2010.

[9]TANG Yong，CHEN Ming，WANG Bo.An improved method for IGBT base excess carrier lifetime extraction[C]//International Conference on Applied Superconductivity and Electromagnetic Devices，2009，September 25 － 27，2009，ChengDu，China.2009:206－210.

[10]唐勇，胡安，陈明.IGBT栅极特性与参数提取[J].电工技术学报，2009，24(7):76 －80.TANG Yong，HU An，CHEN Ming.IGBT gate characteristics and parameter extraction methods[J].Transactions of China E-lectro technical Society，2009，24(7):76 －80.

[11]陈明，汪波，唐勇.IGBT动态热阻抗曲线提取实验研究[J].电力电子技术，2010，44(9):101 －103.CHEN Ming，WANG Bo，TANG Yong.The experimental research on transient thermal impedance of IGBT[J].Power Electronics，2010，44(9):101 －103.

[12]陈明，胡安，唐勇，等.绝缘栅双极型晶体管传热模型建模分析[J].高电压技术，2011，37(2):453－459.CHEN Ming，HU An，TANG Yong，et al.Modeling analysis of IGBT thermal model[J].High Voltage Engineering，2011，37(2):453－459.