基于Metropolis-Hastings算法的α稳定分布参数估计

马洪斌，马岩，杨春梅，沈锋

(1.哈尔滨理工大学 机械动力工程学院，黑龙江 哈尔滨150080;2.东北林业大学 机电工程学院，黑龙江 哈尔滨150040;3.东北林业大学 研究生院，黑龙江 哈尔滨150040;4.哈尔滨工程大学 自动化学院，黑龙江 哈尔滨150001)

0 引言

在传统的信号处理中，由于高斯模型可以很好地描述许多信号噪声并且算法结构简单，通常假定接收机接收的信号噪声为高斯分布白噪声[1]，然而，在实际的情况中所遇到的许多信号或噪声往往具有显著地尖峰脉冲特性，例如水声信号、低频大气噪声、生物医学信号和金融数据等[2－4]。这类信号的统计特性明显区别于高斯信号的分布特点，表现在其概率密度函数具有比高斯分布更厚的拖尾，而且概率密度函数往往是非对称的。在这种背景下，基于高斯假定设计的信号处理系统会出现性能退化。而α稳定分布为这类信号提供了良好的数学模型从而得到广泛的研究和应用[5－9]，α稳定分布是目前惟一的一类满足广义中心极限定理的分布，由于可以描述更加广泛的数据，因此具有更普遍的意义。

α稳定分布参数估计的方法主要有最大似然法、样本分位数法、样本特征函数法和负阶距法等[1，10－11]。最大似然估计法属于复杂的非线性优化问题，没有初始值选择原则和收敛分析可供使用，并且计算量相当可观;样本分位数的方法受到查找表的制约，只能进行模糊估计;特征函数法、负阶距法都可以准确的估计α稳定分布的参数而且计算方便，但是仅适用于对称α稳定分布，无法对偏斜参数β进行估计，实际应用中存在很大的局限性。贝叶斯估计克服了以上缺点，应用MCMC动态模拟的方法在已知待估计参数先验分布的条件下可以准确地估计出α稳定分布的所有4个参数。

1 α稳定分布模型

由于α稳定分布不存在封闭的概率密度函数，所以通常用特征函数来描述。一维的α稳定分布特征函数为

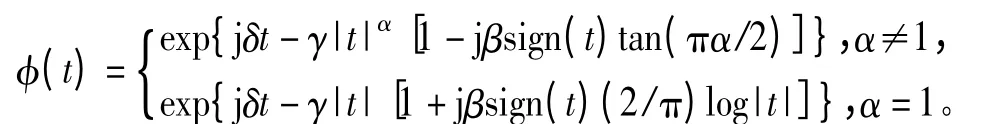
式中:sign(·)为符号函数;参数 α∈(0，2]称为特征指数，他决定该分布脉冲特性的程度。α值越小，所对应分布的拖尾越厚，因此脉冲特性越显著，当α=2时，此分布成为均值为μ方差为2γ的高斯分布。当α=1且β=0时为柯西分布;参数β∈(－1，1)称为偏斜参数，用于确定分布的斜度，β＞0分布右偏，β＜0分布左偏，β=0分布对称，简称为SαS，高斯分布和柯西分布都属于SαS分布;参数γ为分散系数，又称尺度系数，他是关于样本相对于均值的分散程度的度量，由于α稳定分布不存在有限的方差，所以使用分散系数来描述分布的偏离均值的程度;参数δ称为位置参数，对于SαS，在α∈(1，2]时δ表示分布的均值，在α∈(0，1]时表示分布的中值。若随机变量x服从于 α 稳定分布，则记为 x～Sα(γ，β，δ)。

2 α稳定分布的贝叶斯模型

贝叶斯推断的本质就是利用观测数据把参数的先验概率分布转化为相应的后验概率分布。若用X表示观测值，用θ表示未知参数，则未知参数θ的后验概率密度p(θ|X)可根据贝叶斯条件概率准则推出，即

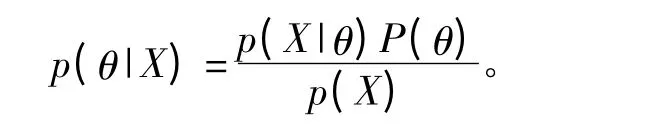
其中:p(θ)是未知量的先验概率密度;p(X|θ)是参数 θ 的似然函数;全概率 p(X)=∫p(X|θ)P(θ)dθ被称为归一化常数，贝叶斯定理可简化表示为p(θ|X)∝p(X|θ)P(θ)，式中∝ 表示两边仅相差不依赖θ的常数因子。因此，把贝叶斯推断中所有的未知参数视为随机变量，利用观测数据的似然函数和未知参数的先验信息通过计算未知参数后验概率密度函数，得到未知参数的估计值。

在利用贝叶斯推断估计α稳定分布的参数时，首先建立α稳定分布的贝叶斯推断模型，未知参数可确定为 θ=(α，β，γ，δ)。假定 α 稳定分布的四个参数相互独立，那么利用贝叶斯层次模型表示为

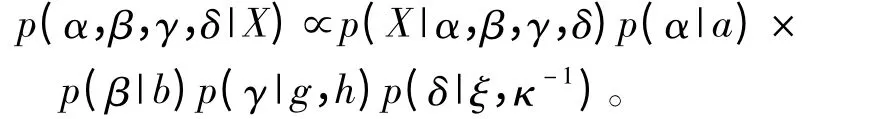
式中，a、b、g、h、ξ、κ 是先验分布的超参数。根据未知参数的分布特点假设参数α，β的先验分布是在定义域内的均匀分布，a，b各为参数 α，β定义域区间长度，参数γ服从以(g，h)为超参数的逆伽马分布，参数δ服从以(ξ，κ－1)为超参数的正态分布，各先验分布为

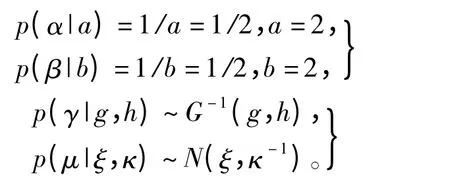
3 基于M－H算法的MCMC模拟

运用贝叶斯方法估计参数时，由于在求解归一化因子的过程中存在多维积分问题，未知参数的后验分布无法求得解析解，因此无法单纯运用在参数估计的过程中，但是应用 MCMC(Markov chain Monte Carlo)[13]的方法解决贝叶斯估计中的多维数值积分问题，MCMC方法是以动态构造Markov链为基础，通过遍历性约束来实现模拟目标分布的一类随机模拟的方法。当应用在贝叶斯估计时，以未知参数的后验分布为目标函数，采用Gibbs采样法或者Metropolis Hastings采样法，通过随机模拟产生收敛到目标函数Markov链，从而得到未知参数的估计值。在实际计算中，采用间隔k个点采样一次，这样可以减小相邻采样点的相关性，得到的样本可以近似看做是独立同分布的样本。

采用M－H采样法对α稳定分布进行参数估计，令 θ=(α，β，γ，δ)构造以当前状态 θ(t)为均值，标准差为σ的正态分布为建议分布即q(·|·)～N(θ(t)，σ)，新候选点 θ*应表示为

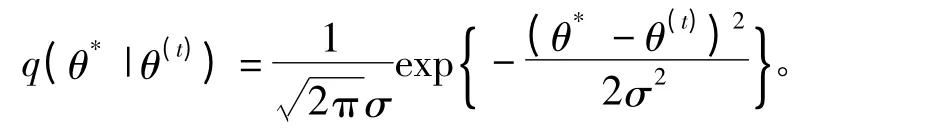
根据α稳定分布的贝叶斯推理模型和M－H算法，可以推导出α稳定分布参数估计的更新过程以及相应的接受概率，以特征指数α为例，具体步骤如下:

1)对于特征指数α，假设Markov链当前状态为(t，α(t))，从提议函数 q(·)抽取候选点 α*，即 α*～ q(α*|α(t))。

2)计算接受概率Aα

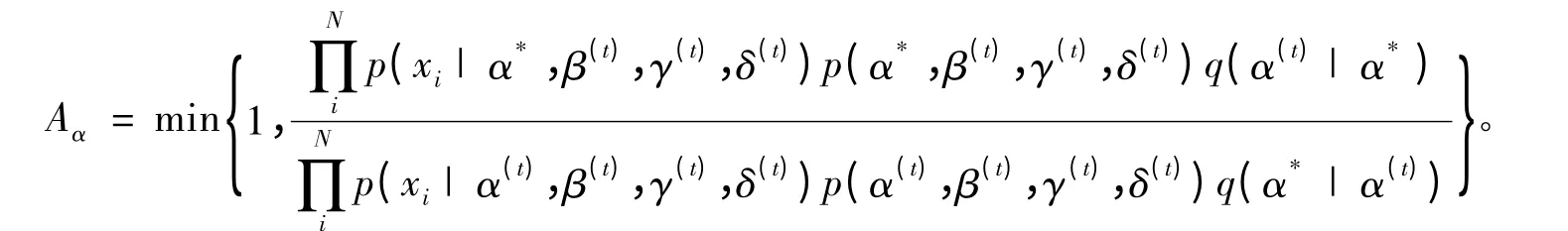
由于(α，β，γ，δ)4 个参数分别独立，则 Aα为

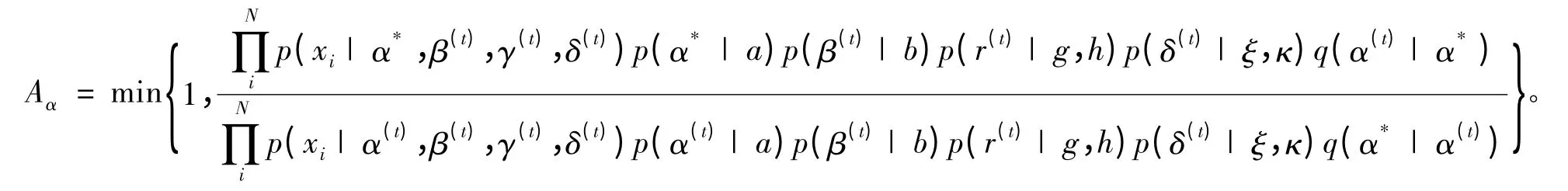
考虑到提议函数为对称分布，且p(α)为均匀先验，那么接受概率可简化为:

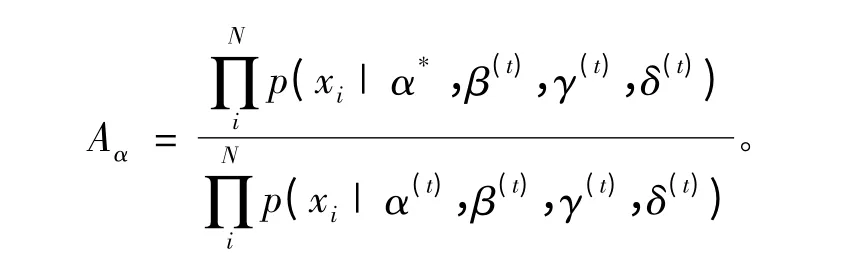
3)生成随机数 u～U(0，1)，如果 u≤Aα则接受候选点α*，Markov链状态值进行更新，否则拒绝候选点，Markov链状态保持不变，然后循环步骤1)，直到目标分布趋于平稳。

对偏斜参数、分散系数和位置参数使用与特征指数相同的策略，令 β*～ q(β*|β(t))，γ*～ q(γ*|γ(t))，δ*～ q(δ*|δ(t))，计算可得接受概率 Aβ，Aγ，Aδ分别为

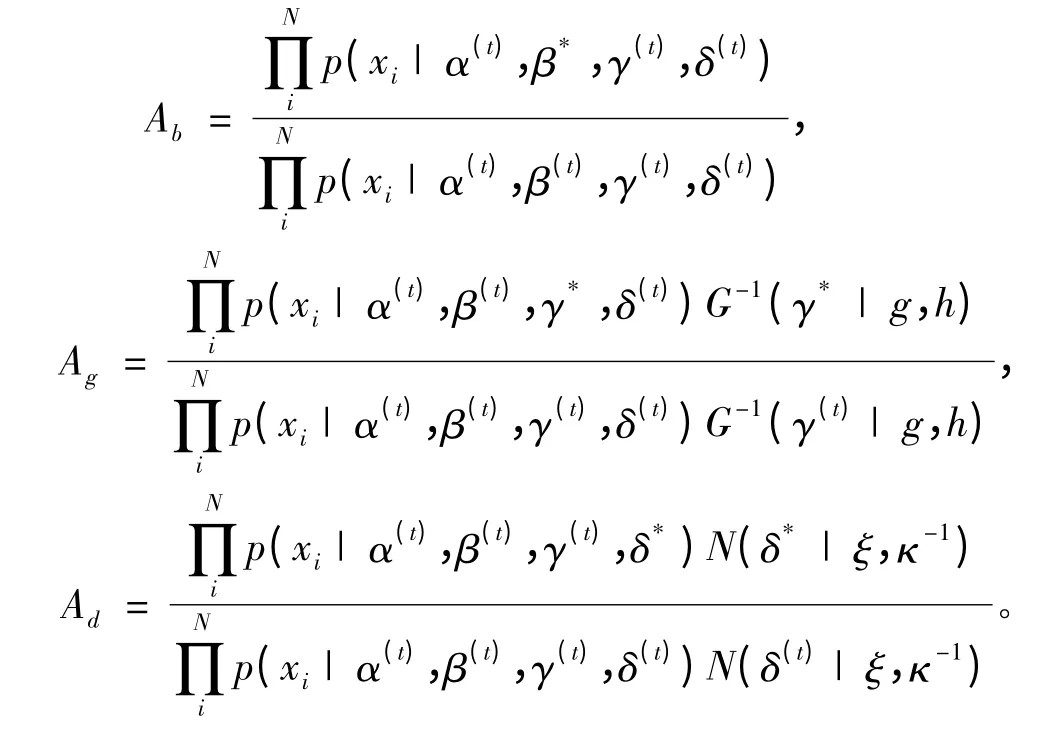
4 仿真结果与分析

4.1 特征指数{α}估计

假设稳定分布参数{β，γ，δ}已知，仅特征指数α未知，当α取不同值时，利用提出的方法对其进行估计。仿真条件设置:在标准稳定分布下(β=0，γ =1，δ=0)，取样本数 N=1 000，迭代次数 10 000，burn－in时间1 000 s，超参数 g=1，h=1，κ =1。当α≤1时 ξ=median(y)，当 α ＞1时 ξ=mean(y)，提议分布的标准偏差σα=0.15。在仿真过程中应用Chambers－Mallows－Stuck的方法产生待估计参数的α稳定分布随机变量，在稳定分布参数为(α=0.6，β=0，γ =1，δ=0)情况下，产生的1 000 个随机样本点如图1、图2所示，可见α稳定分布相比高斯分布具有更强的脉冲特性，在β=0对称的条件下，图2表现出在中心位置的两侧随机样本的数量大致相同。

图3、图4给出了当α取不同值时，特征指数α的估计效果以及Markov链的自相关时间曲线。可见本文提出的参数估计方法对任意特征指数α都有很好的估计效果，Markov链混合性能良好。在提议函数方差不变的情况下，随α值的增大，估值的标准偏差略有增大，而自相关函数值减小，Markov链可以稳定收敛。表1给出了当α取不同值时，初始值α0、估计值、标准偏差 Std.Dev、M －H 接受概率以及自相关时间的统计数据。统计结果表明算法适用于任意α∈(0，2]值的估计，且具有较高的估计精确度。

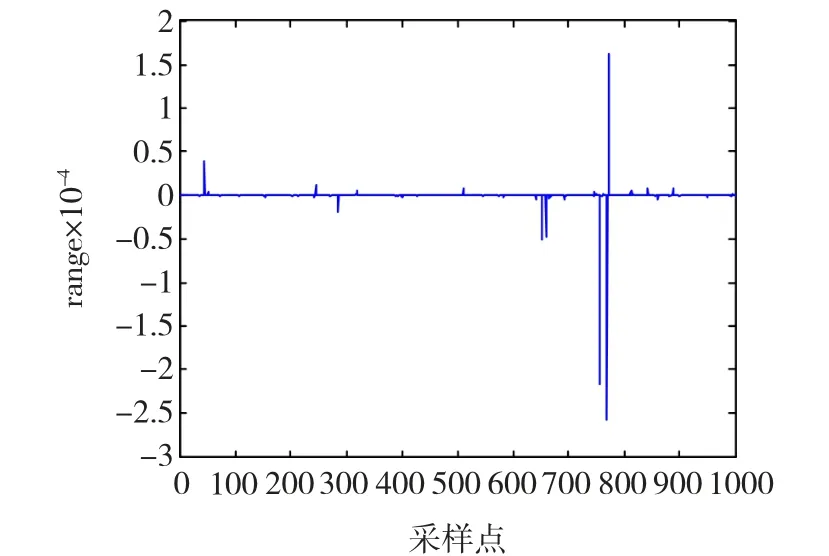
图1 α稳定分布下1 000个随机样本点Fig.1 1000 random variables for α-stable

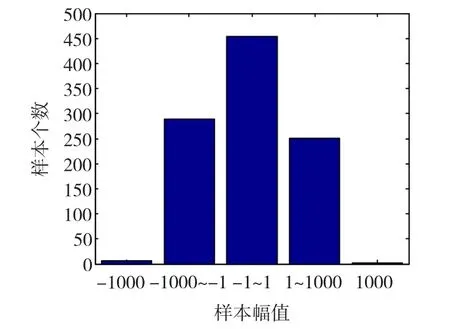
图2 随机样本点分布图Fig.2 Distribution of random variables

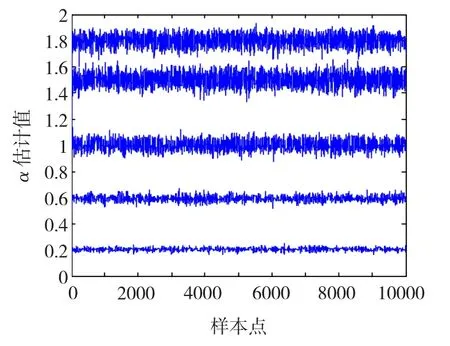
图3 特征指数α的估计效果Fig.3 α estimation results

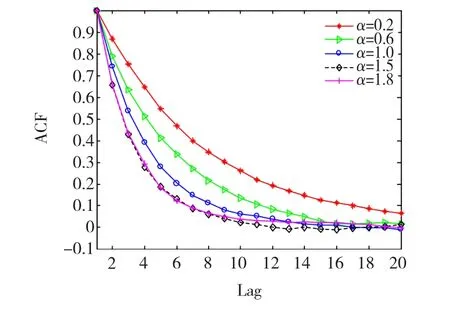
图4 Markov链自相关时间Fig.4 Correlation time of Markov

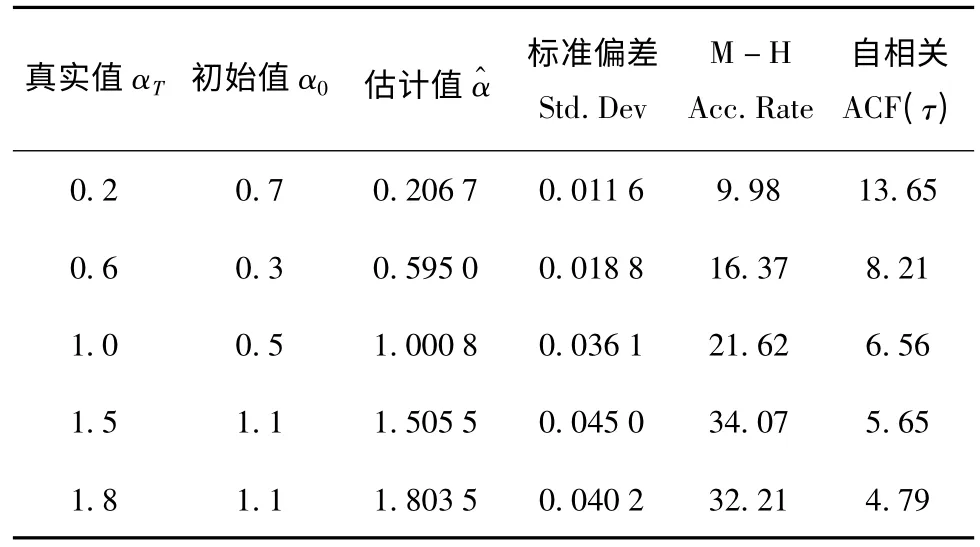
表1 特征指数α的估计效果Table 1 α estimation results

4.2 参数{α，β，γ，δ}联合估计

前面的仿真实验中，均假定参数{β，γ，δ}已知，但一般情况下这种假设是不成立的。在实际应用中，观测值往往反映出分布的某种偏斜特性;当α值较小时，样本均值与真实位置参数也相去甚远，而分散系数也有别于高斯分布的方差，这些都会影响分布模型的准确性，因此必须对其进行可靠的估计。

为了验证提出的方法的正确性，仿真实验按照偏斜参数的不同分两种情况:1)β＜0;2)β＞0。仿真条件设置:样本数N=1 000，迭代次数为10 000，burn－in时间 1 000;超参数 g=1，h=1，κ =1，当α≤1时 ξ=median(y)，当 α ＞1时 ξ=mean(y)，提议函数的标准偏差 σ ={0.15，0.1，0.1，0.2}。

图5和图6给出了两组仿真实验的参数估计效果。从中可以发现，在不同的仿真条件下，Markov链都有良好的混合性能，表现为在支撑域附近强烈的摆动，每条链均可靠的收敛到目标分布，准确地估计出了特征指数α、偏斜参数β、分散系数δ和位置参数δ。两组仿真实验综合 α＜1和α＞1，以及β＜0、β＞0典型情况，因此测试结果表明该方法对具有不同偏斜特性的任意α稳定分布参数的组合都适用，且估计性能不受参数取值范围的限制。另外，从图中可以看出，由于参数之间的相互影响以及不同的α稳定分布参数组合结构，使得在给定的提议函数和不变方差条件下，估计值会有不同的标准偏差。表2给出了上述3种情况下，α 稳定分布参数的真实值 θT、初始值 θ0、估计值、标准偏差、M－H接受概率和自相关时间的统计数据。统计结果也表明，提出的方法不仅实现了任意特征指数α的准确估计，而且他能够以同样的精度估计出偏斜参数β、分散系数γ以及位置参数δ，这一点在实际应用中是非常重要的，但传统的方法往往无法实现。

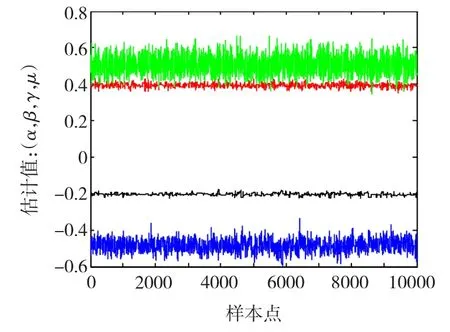
图5 参数联合估计效果(β＜0)Fig.5 Joint parameters estimation result(β ＜0)

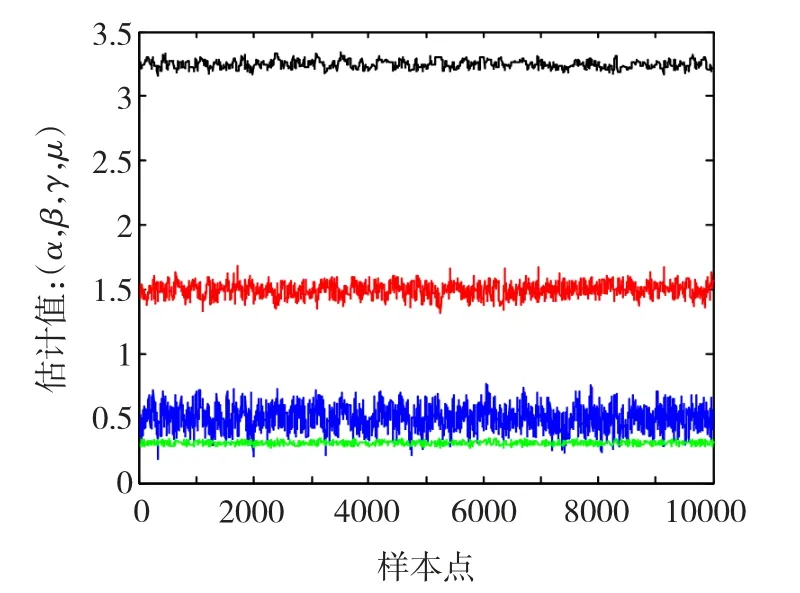
图6 参数联合估计效果(β＞0)Fig.6 Joint parameters estimation result(β ＞0)

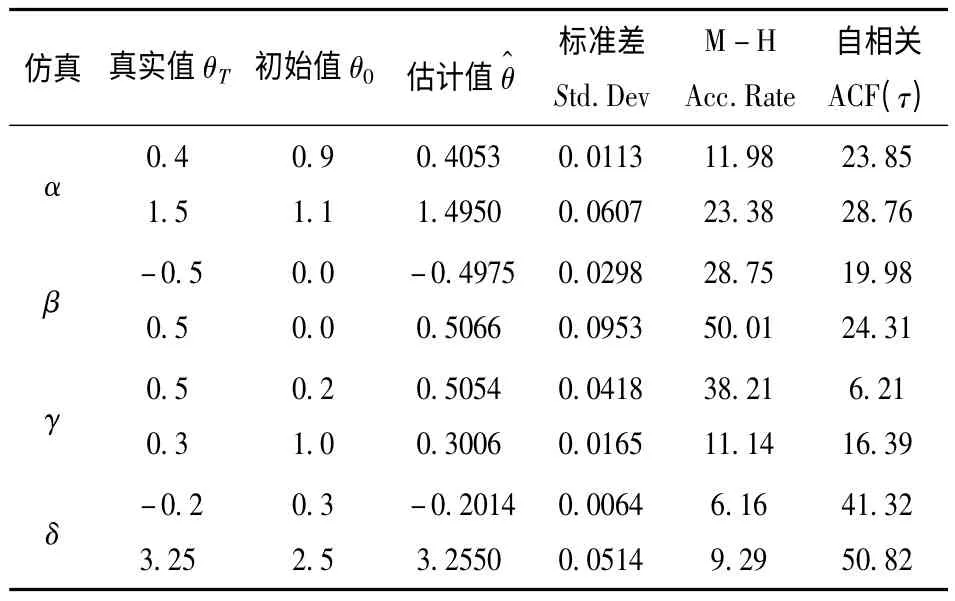
表2 参数估计效果Table 2 Parameters estimation result

5 结语

α稳定分布可以很好地描述具有显著尖峰脉冲波形和重尾的非高斯现象，是一种非常有效的统计信号处理工具。本文针对非对称α稳定分布参数估计问题，在贝叶斯统计推理的框架下，提出一种基于MCMC动态模拟的参数估计新方法。该方法实现了对任意α稳定分布参数的估计，参数估计精度高且不受取值范围的限制，特别是它克服了传统方法无法估计偏斜稳定分布的不足。同时需要指出的是，本文的估计结果是在Markov链可靠收敛，提议函数合理有效的前提下给出的，如何设计更好的提议函数，增加算法效率以及开发利用α稳定分布解决实际问题将是下一步的研究重点。

[1]HAO M，NIKIAS C L.Signal processing with fractional lower order moments:stable processes and their applications[J].Proceedings of the IEEE，1993，81(7):986－1010.

[2]ROENKO A A，LUKIN V V，DJUROVIC I.Two approaches to adaptation of sample myriad to characteristics of SαSdistribution data[J].Signal Processing，2010，90:2113 －2123.

[3]SALAS Gonzalez D，KURUOGLU E E，RUIZ D P.Modelling with mixture of symmetric distributions using Gibbs sampling[J].Signal Processing，2010，90:774－783.

[4]司伟建，蒋鹏，刘旭波.改进的三次相位函数法LFM雷达信号参数估计[J].哈尔滨工程大学学报，2012，33(6):771－774.SI Jianwei，JIANG Peng，LIU Xubo.The parameter estimation of an LFM radar signal based on a modified cubic phase function[J].Journal of Harbin Engineering University，2012，33(6):771－774.

[5]ARIKAN O，BELGE M，CETIN A E，et al.Adaptive filtering approaches for non-gaussian stable process[C]//International Conference on Acoustics，Speech，and Signal Processing，ICASSP －95，1995，2:1400－1403.

[6]TSIHRINTZIS G A，NIKIAS C L.Evaluation of fractional lowerorder statistical-based detection algorithm on real sea-clutter data[J].IEE Proceedings on radar，sonar navigation，1997，144(1):29－38.

[7]MA X，NIKIAS C L.Joint estimation of time delay and frequency delay in impulsive noise using fractional lower order statistics[J].IEEE Trans on Signal Processing，1996，44(11):2669－2687.

[8]朱晓波，王首勇，李旭涛，等 非高斯杂波中的MIMO雷达信号分离[J].系统工程与电子技术，2010，32(6):1210－1214.ZHU Xiaobo，WANG Shouyong，LI Xutao，et al.MIMO radar signal separation in non-Gaussian clutter[J].System Engineering and Electronics，2010，32(6):1210 －1214.

[9]唐洪，邱天爽.Alpha稳定分布噪声环境下广义恒模算法收敛性能的研究[J].电子学报，2009，37(1):118－121.TANG Hong，QIU Tanshuang.Convergence properties of the GCMA in alpha-stable noise environment[J].Acta Electronics Sinica，2009，37(1):118 －121.

[10]KURROGLU E E.Signal Processing in alpha-stable Noise Environments:A Least lp-Norm Approach[D].University of Cambridge，1998.

[11]LOMBARDI M J.Bayesian inference for α-stable distributions:A random walk MCMC approach[J]，Computational Statistics＆Data Analysis，2007，51:2688－2700.

[12]SALAS Gonzalez D，KURUOGLU E E，RUIZ D P.Finite mixture of α-stable distributions [J]，Digital Signal Processing，2009，19:250－264.

[13]LAINE M.Adaptive MCMC methods with applications in environmental and geophysical models[D].Finnish Meteorological Institute Helsinki，2008.