超临界汽轮发电机定子股线堵塞对温度分布的影响

管春伟，李伟力，郑萍

(1.哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨150001;2.北京交通大学 电气工程学院，北京100044)

0 引言

与亚临界机组相比，超临界机组具有煤耗低，效率高，温室气体排放少等优点，且机组容量愈大效益越明显。机组容量的增大，与之配套的汽轮发电机的功率也随之增加，所以开展大容量超临界汽轮发电机的研究具有重要的意义。

大容量汽轮发电机定子绕组多采用水内冷，且采用空心股线和实心股线混合排列，绕组结构的复杂性增加了发电机内电磁和温度计算的难度。与传统绕组相比，空心股线的存在，将引起发电机定子股线涡流损耗分布的改变，进而直接影响定子温度的变化。在发电机运行过程中，空心股线的堵塞会造成电机的局部过热，加快主绝缘的老化，严重时还会将绝缘击穿，造成发电机短路而停机。因此，1000MW超临界汽轮发电机的电磁场和温度场的研究对于预测电机的全局温度分布及故障状态下的局部温度分布具有重要的意义。

目前，对于水内冷发电机定子空心股线堵塞情况下温度场的相关研究较少。文献[1－6]对发电机正常运行状态下的温度场进行了研究;文献[7]采用热网络方法对发电机断水持续运行30s后的温度进行了计算;文献[8－9]采用热网络方法研究了定子线棒一根空心股线的冷却水路发生堵塞后定子温度分布。

本文采用共轭传热法对发电机正常和股线堵塞故障下的定子流体场与温度场进行了求解，在求解过程中考虑了大容量汽轮发电机空实心股线涡流损耗分布对温度计算结果的影响。将采用有限元法得到的每根股线的涡流损耗作为温度场热源，减小了损耗计算不准对温度计算结果的影响。研究了定子空心股线堵塞根数和堵塞位置对电机定子温度分布的影响，通过不同堵塞方案下温度结果的对比分析，提出了一种可以有效降低发电机定子最高温度的绕组新结构。绕组采用该新结构，当发电机发生股线堵塞故障时，发电机的最高温度较原结构明显降低，能够保证发电机长时间运行，为排除故障争取了时间，也降低了由于局部温度过高发电机停机而产生的损失。

1 1000MW超临界汽轮发电机额定工况下定子流体场与温度场计算分析

1 000 MW超临界汽轮发电机采用的是水－氢－氢的冷却方式，定子绕组采用实心股线和空心股线混合排列的方式，定子空心股线的内部通水进行冷却，定子径向通风沟采用氢气冷却。该1 000 MW汽轮发电机转子极数为2极，额定功率1 000 MW，定子额定电流23 950 A，额定电压27 kV，额定功率因数0.9，定子槽数42。

1 000 MW超临界汽轮发电机定子绕组采用空心股线与实心股线混合排列的非传统方式，为减小股线涡流，上下层股线采用不等股不等截面结构。由于涡流损耗受实心股线和空心股线排列方式的影响较大，为了更准确的计算温度场，对发电机定子槽内上下层空心和实心股线涡流损耗进行了数值计算[10－13]，将计算得到的股线涡流损耗结果作为温度场的热源。

受槽内漏磁场和股线截面积大小的影响，下层股线的涡流损耗较上层股线的要低，上层实心股线电阻增大系数最大值为1.42，而位于槽口处的空心股线最大电阻增大系数为3.1，远大于实心股线的电阻增大系数。其中上层线棒平均电阻增大系数为1.672，下层线棒平均电阻增大系数1.167，整体平均电阻增大系数为1.438。图1为发电机每根股线的交流电阻增大系数，股线编号从槽底开始到槽口。

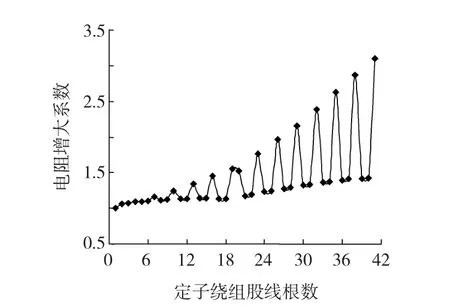
图1 1 000 MW超临界水—氢—氢汽轮发电机定子绕组电阻增大系数数值计算结果Fig.1 Resistance enhancement coefficient by using numerical method for 1 000 MW turbo-generator

考虑到电机结构的对称性，确定了定子共轭传热的物理求解域模型如图2所示。由于本文主要分析定子水内冷发电机股线堵塞状态下定子的温度分布，在计算过程中考虑了定子股线绝缘与排间绝缘对定子温度分布的影响，以及空心股线冷却能力对股线绝缘性能的影响程度，在有限元建模过程中，将定子股线绝缘、排间绝缘进行了单独的建模处理。由于股线绝缘的尺寸较小，造成了有限元离散过程中网格数量过多，为了减小求解量，将求解区域限定在一个通风沟两侧的一个铁心段，周向一个齿距的范围。

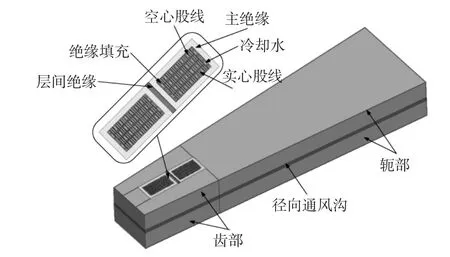
图2 1 000 MW超临界水－氢－氢汽轮发电机定子共轭传热求解域Fig.2 Liquid-solid conjugate heat transfer model for 1 000 MW turbo-generator

大容量汽轮发电机热分析涉及到流体场与温度场的耦合求解，在求解的过程中，需要同时满足式(1)～式(3)质量守恒方程，动量守恒方程和能量守恒方程。根据流体力学理论，对电机内的径向通风沟的流体采用标准 k－ε方程进行描述[14－17]。

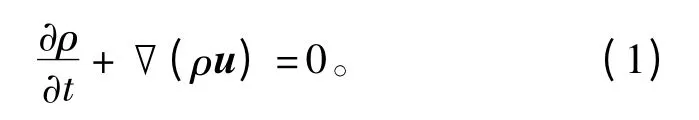
式中:ρ为流体密度，单位为 kg/m3;t为时间，单位为s;u为流体的速度矢量。

式中:F为流体受到的质量力，单位为N;p为流体压力，单位为pa;μ为流体的粘性系数。

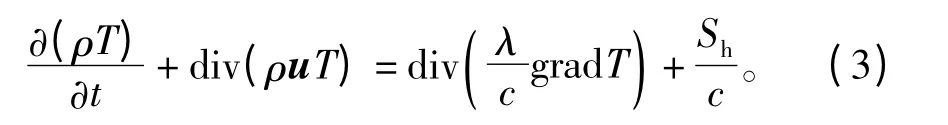
式中:T为温度，单位为℃;λ为导热系数，单位为W·m－1·K－1;c为比热容，单位为 J·kg－1·℃－1;Sh为体积生热率，单位为W·m－3。

采用标准湍流k－ε模型对流体进行描述，当流体不可压缩且处于稳定流动状态时，通用控制方程为

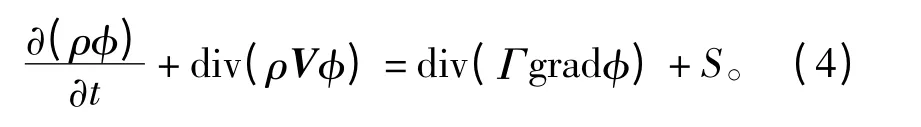
式中:φ、V为通用变量;Γ为扩散系数;S为源项。

在发电机流体场与温度场求解过程中，作基本假设如下:

1)电机中流体的雷诺数很大(Re＞2 300)，流体属于湍流，采用湍流模型对电机内流体场进行求解;

2)发电机径向通风沟采用氢气冷却，根据冷却氢气总流量，计算得到径向通风沟入口速度为18 m/s;

3)发电机定子绕组采用水冷却，根据绕组入口水流量，得到进入每根空心股线的入口流速为1.5 m/s。

4)考虑到结构的对称性，认为定子齿中心面和通风沟两侧的铁心段中心截面为绝热面。

5)定子股线热源为定子绕组基本铜耗和附加损耗，齿部和轭部热源为定子铁损。

通过对该微分方程的边值问题进行求解，得到了定子不同部位的流速和温度分布。图3为发电机径向通风沟中心截面氢气的流速分布。

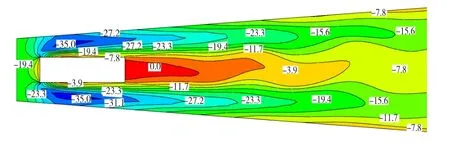
图3 径向风沟中心截面处流速分布图(m/s)Fig.3 Velocity distribution of hydrogen in ventilation duct(in m/s)

从图3中可以看出定子通风沟最高流速为37.8 m/s，由于线棒的扰流作用，在槽底部位出现了尾流，此处的流速较低。然而，由于氢气的密度较小，扩散性较好，尾流的区域较小，在定子外圆处，流速在周向分布已经趋于均匀。由于定子冷却水对绕组的冷却效果较氢气对齿部的冷却效果要好，绕组的绝大部分热量由冷却水带走，因此正常情况下绕组的温度较齿部的温度要低，电机的最高温度出现在定子齿部，最高温度为90.4℃，如图4所示。

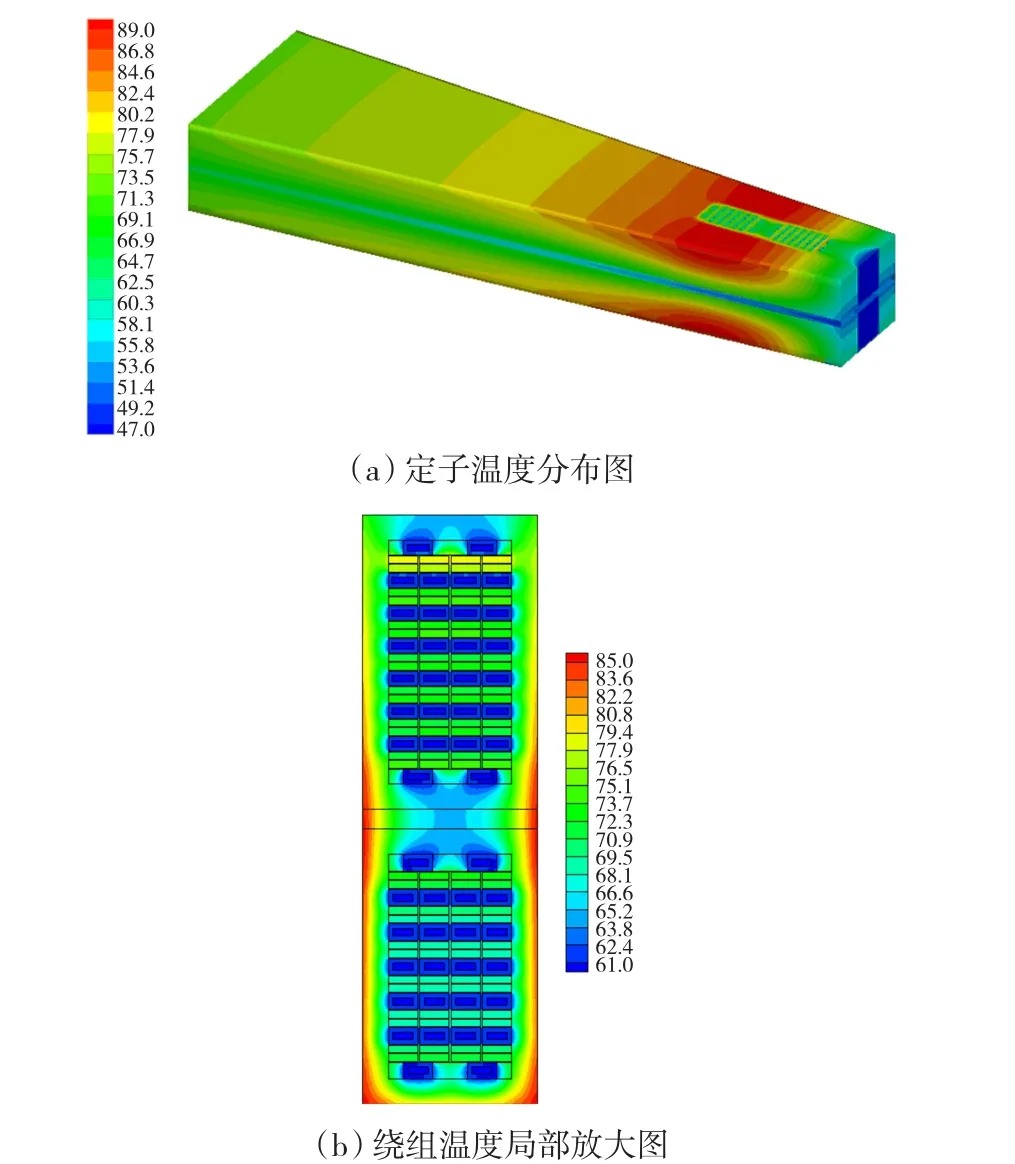
图4 1 000 MW超临界水－氢－氢汽轮发电机额定负载定子温度(℃)Fig.4 Stator temperature of 1 000 MW supercritical turbo-generator under rated load

图4为发电机额定工况下定子绕组的温度分布图，其中图4(b)给出了定子上下层线棒的温度局部放大图。由于发电机定子线棒采用两行实心股线上面布置一行空心股线进行冷却，因此从图中可以看出位于空心股线处的温度分布明显较低。与空心股线冷却方式不同，实心股线非直接冷却，而是通过热传导的方式将热量传递出去，因此温度较空心股线的区域要高，整个绕组的温度呈现一高一低的分布规律。

图5为发电机主绝缘在径向方向上内外侧温度分布图，其中图5(a)中主绝缘位于电机轴向铁芯段的绝热面处，图5(b)中主绝缘位于电机轴向通风沟处。由于定子冷却水的热传导性较好，空心股线产生的热量大部分被冷却水带走，使得空心股线的温度较低，图中主绝缘内侧温度呈现脉动趋势正是由于空心股线和实心股线混合排列引起的。

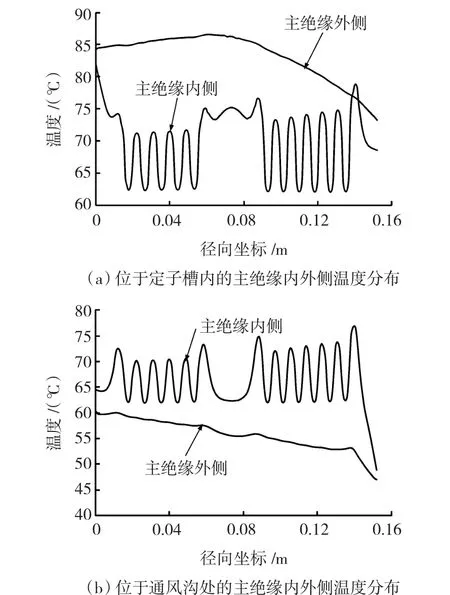
图5 发电机正常运行不同位置处的绝缘温降分布曲线(℃)Fig.5 Insulation temperature drop at different position of 1 000 MW turbo-generator

将采用数值方法计算得到的电机温度结果与实测值进行对比，如表1所示。计算值与实测值比较接近，说明了本文计算方法的正确性。

表1 正常情况下电机温度计算与实测结果Table 1 Calculated and test temperature results under normally conditions ℃

2 1 000 MW超临界汽轮发电机定子空心股线堵塞情况下温度场分析

水内冷汽轮发电机在运行过程中常发生冷却股线堵塞的问题，造成发电机绕组局部温度过高，严重时甚至停机检修，给发电机及电网的安全运行带来隐患。本文对定子空心股线堵塞情况下电机温度场和流体场进行了计算，在计算过程中，定子线棒冷却水总流量保持不变，其中的一根空心股线堵塞后，其他空心股线进水流量相应增大。定子空心股线单根堵塞后，其它空心股线的入口流速变为1.532 m/s，空心股线两根堵塞后，其它空心股线的入口流速变为1.563 m/s。根据上述对电机槽内涡流场的计算得知，受槽内漏磁场的影响，上层线棒的涡流损耗明显大于下层线棒的，对绕组内温度分布的影响也较大。因此，在对空心股线堵塞情况下的温度场计算中，只考虑了上层线棒空心股线堵塞这种较严重的情况，对下层空心股线堵塞后的温度分布没有进行计算。在计算过程中，假定发电机运行过程中发生堵塞的股线具体位置及编号如图6所示，分析了堵塞股线不同位置对定子温度分布的影响。

图6 上层线棒股线堵塞不同方案分布图Fig.6 Positions and numbers of blocked hollow strands in upper windings

认为空心股线堵塞分两种情况，一种为上层线棒仅有一根空心股线发生堵塞，堵塞的位置分别为2号空心股线，7号空心股线和8号空心股线。另一种为上层线棒2根空心股线同时发生堵塞，堵塞的股线具体位置分别为1、2 号，3、7 号，4、7 号、5、7 号，7、8 号和8、9号，定子温度计算结果如表2和表3所示。

定子线棒发生单根股线堵塞时，绕组温度明显升高，绕组的温升变化大小与发生堵塞股线的位置密切相关。从表1可以看出，当电机正常运行时，绕组的最高温度为79.2℃，齿部最高温度为90.4℃。表2中，当2号、7号和8号空心股线发生堵塞时，电机绕组的最高温度分别变为106℃，98.8℃和138℃，最高温度出现在堵塞的空心股线位置处。由于三种堵塞情况中7号股线所在位置为4根空心股线并排，其周围冷却效果比2号和8号股线所在的位置要好，堵塞时温度相对较低。而在2号和8号股线处，冷却的股线为2根并排，因此股线周围的冷却效果较差，而且定子线棒最上层空心绕组的涡流损耗最大，因此8号股线发生堵塞时绕组的温度升高最多，此时绝缘的温度较正常情况下要高49℃。由于局部温度过高，此种情况极易造成主绝缘的局部老化。图7(a)为第8根股线堵塞时上层线棒温度分布图。

表2 单股股线堵塞时定子不同部位最高温度(℃)Table 2 Highest temperature of different parts with single strand blocking

表3为定子上层绕组第8根和第9根股线同时堵塞时定子不同部位的温度计算结果，图7(b)为此种情况下上层线棒绕组温度分布图。从计算结果可以看出，由于最上层空心绕组受到定子槽内漏磁场的影响，会产生较大的涡流损耗，当最上面2根空心股线同时堵塞时，绕组的最高温度能够达到152℃，主绝缘温度达到150℃。该1 000 MW超临界汽轮发电机定子采用F级绝缘，当第8根和第9根股线同时发生堵塞时，电机主绝缘的温度已经接近极限，这对电机绝缘寿命及电机的安全运行会造成严重影响。因此，采用这种绕组排列方式的发电机，应该避免发生上层线棒最上面两根空心股线同时堵塞。一旦在此处两根股线同时发生堵塞，会引起绕组局部和主绝缘温度过高，加快绝缘老化和由于温度分布不均引起的热应力对绝缘造成的损害，严重危害电机的寿命及机组的安全运行。

表3 双根股线堵塞上层线棒不同部件最高温度(℃)Table 3 Highest temperature of different parts with double strands blocking

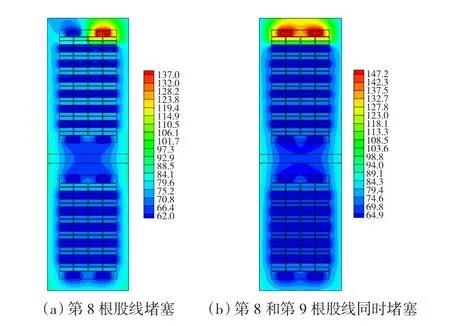
图7 股线堵塞时定子线棒温度分布(℃)Fig.7 Stator winding temperature with blocked hollow strands

3 定子绕组冷却结构优化后发电机正常运行及股线堵塞后定子温度场分析

通过上节对堵塞状态下定子股线区域温度的分析，发现1 000 MW超临界汽轮发电机上层线棒第8根和第9根空心股线同时发生完全堵塞时，会造成电机股线温度的升高，主绝缘温度接近极限值。为此，对定子绕组重新进行了排列，采用新的结构来对电机内部进行冷却，新结构如图8所示。

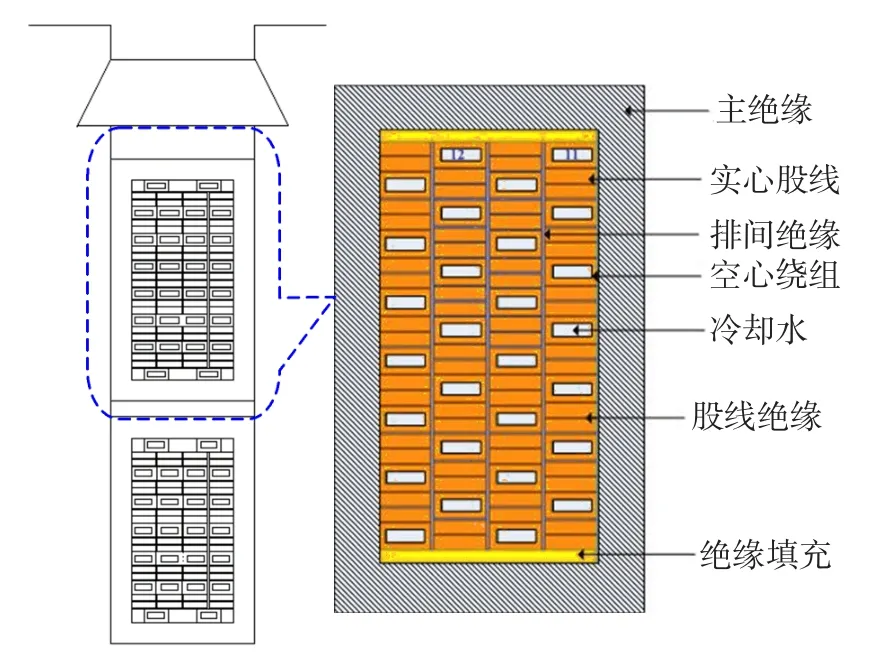
图8 定子绕组冷却结构优化结构Fig.8 Optimized cooling structure of stator windings

将发电机定子绕组原结构与新结构进行对比，可以发现原结构采用的是一行空心股线和两行实心股线混合排列的方式，绕组排布比较有规律。新结构打破了原来的比较规律化的排布方式，采用的是类似棋盘式的排布方式，空心股线不会出现在同一行，而是均匀的分布在整个绕组区域，其优势是在正常情况下能够使绕组的温度分布更加趋于均匀，当发生堵塞故障时，也能够有效降低堵塞股线的温度。

由于定子空心股线和实心股线排列方式的改变，定子绕组附加损耗也发生了变化，通过数值方法重新计算得到了新结构下每根股线的涡流损耗，上层实心股线电阻增大系数最大值为1.37，而位于槽口处的空心股线最大电阻增大系数为3.03。其中上层股线平均电阻增大系数为1.567，下层股线平均电阻增大系数1.085，整体平均电阻增大系数为1.345。

将股线涡流损耗计算结果作为温度场计算的热源，对绕组结构改变后的定子流体场与温度场进行求解，新结构额定工况下温度分布如图9所示。

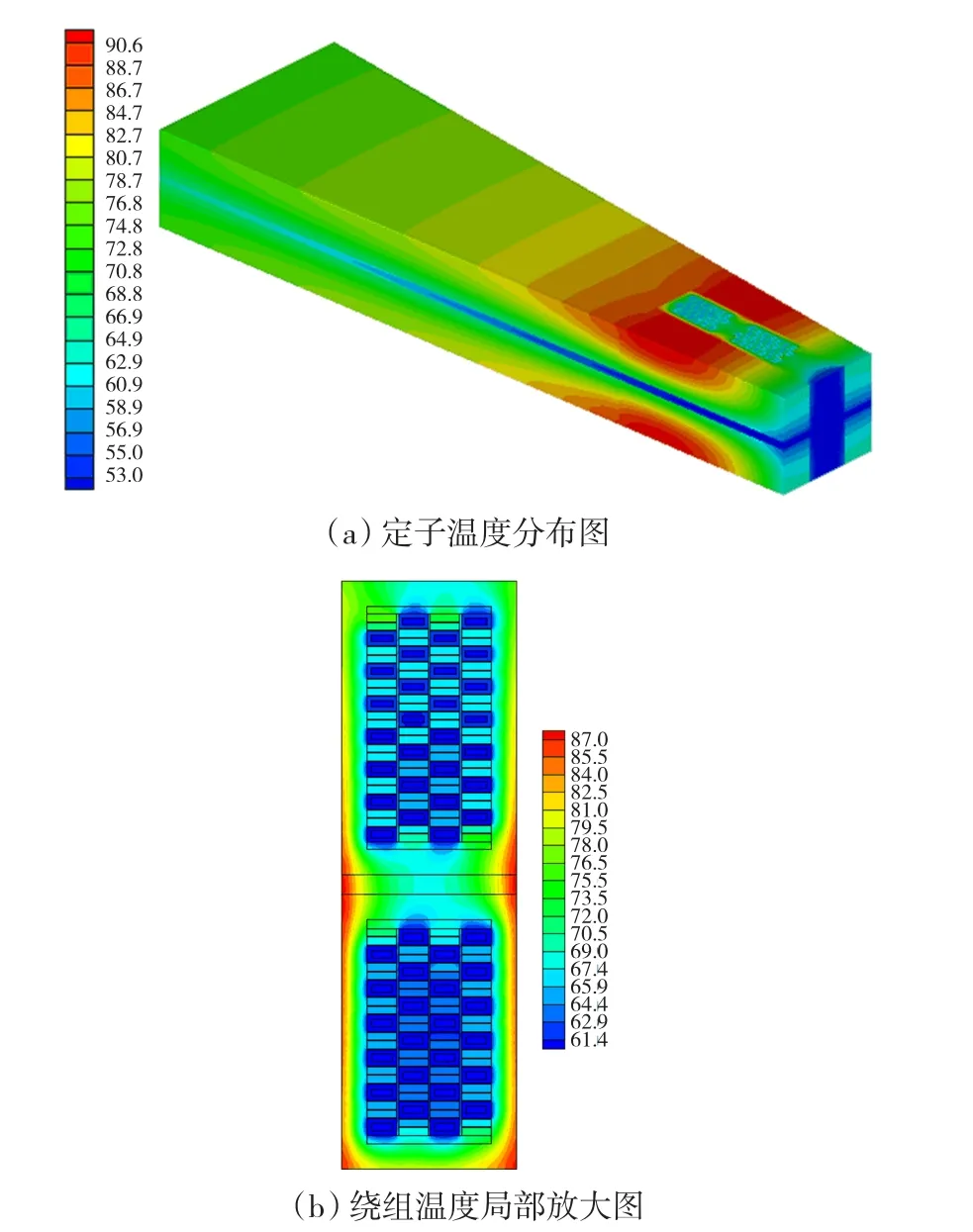
图9 定子空实心绕组结构化后定子温度分布(℃)Fig.9 Stator temperature with optimized stator windings

图9 (a)为新结构下定子区域的温度分布，从计算结果来看，绕组排布改变后，在正常运行情况下，电机齿部温度较原结构升高2℃。图9(b)为定子绕组结构改变后绕组区域温度局部放大图，由于新结构定子空心股线与实心股线进行了交叉排列，使绕组的温度分布更加均匀，实心股线的温度也较原结构有所降低。

从图8可以看出，由于棋盘式绕组排列方式，新结构绕组左右不对称，因此左右两侧的主绝缘温度分布也将是非对称分布。图10给出了新结构下主绝缘左侧和右侧内外表面的温度分布。由于图10中右侧主绝缘靠近槽口位置与第11根空心股线相接触，冷却效果较好，而左侧靠近槽口处的主绝缘与实心股线相接触，冷却效果较差，因此左主绝缘内侧槽口处的温度要高于右主绝缘内侧的温度，图10(a)和(b)中横坐标为0.14处的温度曲线分布也解释了这一现象。

将图5(a)与图10进行对比，可以看出两种结构的发电机主绝缘内侧温度都呈现波浪状，这是受到空心股线和实心股线混合排列的影响。横坐标中间区域为层间绝缘，由于该处受空心股线的冷却影响较小，因此此处温度较高。从对比中还可以看到，图10中，主绝缘内侧的波浪线抖动程度较小，说明新结构下空实心股线的温差较小，与绕组相接触的主绝缘内侧温度变化较平缓，新结构更有利减小主绝缘受热应力不均所受到的损害。

图10 发电机定子结构优化后主绝缘温降分布曲线(℃)Fig.10 Insulation temperature drop at different position with optimized stator windings

通过上节对原始结构发电机堵塞故障下定子温度场的分析，发现发生单根股线堵塞时，最高温度为138℃，出现在上层线棒距离定子槽口最近的股线上。当发生两根股线同时堵塞时，最高温度为152℃，为距离槽口最近的两根股线同时堵塞时出现的。因此，定子绕组采用新结构下，在对空心股线堵塞后的温度场进行分析时，为了减小计算量，只分析了两种情况，分别是:图8中第11根空心股线单根堵塞和第11和12根空心股线同时堵塞。计算后，得到两种堵塞情况下的定子温度分布如图11所示。

定子绕组采用新结构后，当最上面第11根空心股线发生完全堵塞时，绕组的最高温度为101℃，较原始结构最高温度138℃降低了37℃。当最上面第11和12根空心股线同时发生堵塞时，绕组最高温度为105℃，较原始结构的152℃降低了47℃，说明了在发生局部堵塞故障情况下，优化后的绕组结构能够有效降低股线内部的温度，遏制绝缘老化的发生。

图11 定子绕组结构优化后绕组发生堵塞情况下定子线棒温度分布(℃)Fig.11 Stator temperature with optimized stator windings under blocking conditions

4 结论

1)受到空心股线排列方式的影响，定子主绝缘内侧温度呈现波浪状分布。在定子槽内绝热面处的主绝缘，其外侧温度高于内侧温度。而位于通风沟处的主绝缘，其外侧温度低于内侧温度。通风沟处的主绝缘温降与定子槽内绝热面处的主绝缘温降呈现相反的趋势。

2)定子空心股线发生堵塞时，堵塞区域温度明显升高，最高温度与股线堵塞的位置以及发生堵塞股线的数量有关系。当上层线棒单根股线堵塞时，绕组最高温度达到138℃。当最上面两根股线同时被堵塞时，电机绕组的最低温度为99℃，而最高将达到150℃，应避免上层线棒最上面两根空心股线同时堵塞情况的发生。

3)提出了一种棋盘式空心股线新结构，采用该新结构能够使发电机在正常运行时，绕组温度分布更均匀。当发生空心股线堵塞时，与原结构相比，绕组最高温度可以降低47℃，有效防止股线堵塞状态下发电机绝缘老化现象的发生。

[1]焦晓霞，管春伟，李伟力，等.汽轮发电机不同冷却介质对定子传热特性的影响[J].电机与控制学报，2011，15(2):54－62，70.，，，ent cooling medium in turbo-generator on stator heat transfer characteristics[J].Electric Machines and Control，2011，15(2):54 －62，70.

[2]路义萍，丰帆，王佐民，等.同步电机定子三维温度场数值模拟.电机与控制学报，2012，16(3):42 －46.LU Yiping，FENG Fan，WANG Zuomin，et a1.Numerical simulation of 3D temperature field for the stator of a synchronous machine[J].Electric Machines and Control，2012，16(3):42 － 46.

[3]夏海霞，李桃，倪光正.发电机通风系统流场及转子温度场分析[J].电机与控制学报，2007，11(5):472 －476.XIA Haixia，LI Tao，NI Guangzheng.Analysis of ventilation field and rotor temperature field of a generator[J].Electric Machines and Control，2007，11(5):472 －476.

[4]霍菲阳，李勇，李伟力，等.大型空冷汽轮发电机定子通风结构优化方案的计算与分析[J].中国电机工程学报，2010，30(6):69－75.HUO Feiyang，LI Yong，LI Weili，et a1.Calculation and analysis on stator ventilation structure of different optimum proposal in aircooled turbogenerator[J].Proceedings of the CSEE，2010，30(6):69－75.

[5]温志伟，傅德平，顾国彪.浸润式混合强迫内冷的蒸发冷却汽轮发电机定子三维温度场的仿真分析[J].电工电能新技术，2006，25(3):13 －17.WEN Zhiwei，FU Deping，GU Guobiao.Simulation of 3D temperature distribution of immersion evaporative cooling turbo-generator combined with forced inner cooling system[J].Advanced Technology of Electrical Engineering and Energy，2006，25(3):13 －17.

[6]王红宇，李和明，罗应立，等.三峡水轮发电机全定子非线性热—流体耦合网络模型研究[J].中国电机工程学报，2008，28(8):136－142.WANG Hongyu，LI Heming，LUO Yingli，et al.Research on the nonlinear thermal-liquid coupled network model of whole stator of three-gorge generator[J].Proceedings of the CSEE，2008，28(8):136－142.

[7]赵昌宗.三峡水轮发电机定子线圈断水运行能力分析[J].东方电气评论，2004，18(1):1 －3，14.ZHAO Changzong.Analysis of three gorges hydro generator capacity in the envent of loss of stator coil cooling water flow[J].Dongfang Electric Review，2004，18(1):1 －3，14.

[8]李俊卿，王丽慧.汽轮发电机空心股线堵塞时定子温度场的数值仿真[J].中国电机工程学报，2009，29(12):70 －74.LI Junqing，WANG Lihui.Numerical simulation of temperature field in turbo-generators stator on cooling water blockage[J].Proceedings of the CSEE，2009，29(12):70 －74.

[9]李俊卿，李和明.汽轮发电机定子冷却水路堵塞时的温度场分析与计算[J].中国电机工程学报，2005，25(21):163 －168.LI Heming，LI Junqing.Analysis and calculation of turbogenerators stator temperature field on cooling circuit blocked[J].Proceedings of the CSEE，2005，25(21):163 －168.

[10]李伟力，孙宏丽，于海涛.空冷汽轮发电机定子绕组异结构下的不饱和同步电抗、绕组内涡流场与温度场的计算与分析[J].电工技术学报，2011，26(2):50 －58.LI Weili，SUN Hongli，YU Haitao.Calculation and analysis of unsaturated synchronous reactance，eddy current distribution in windings and temperature field for air cooled turbo－generator with different stator windings structures[J].Transactions of China Electrotechnical Society，2011，26(2):50 －58.

[11]程福秀，林金铭.现代电机设计[M].北京:机械工业出版社，1993:169－179.

[12]汤蕴璆.电机内的电磁场[M].北京:科学出版社，1998:218－219，265 －266，270 －273.

[13]谢德馨.用有限元法计算矩形槽内载流导体的集肤效应[J].哈尔滨电工学院学报，1981，4(1):7－23.XIE Dexin.Calculation of the skin effect in the current-carrying rectangular conductor with the finite element method[J].Journal of Harbin Electrician，1981，4(1):7 －23.

[14]王福军.计算流体动力学分析－CFD软件原理与应用[M].北京:清华大学出版社，2004:7－10，120－124.

[15]章梓雄，董曾南.粘性流体力学[M].北京:清华大学出版社，1998:48－142.

[16](美)J.P.霍尔曼(J.P.Holman).传热学(英文版原书第 9版)[M].北京:机械工业出版社，2005:3－12，218－228.

[17]LI Junqing，LI Heming.A thermal model for the water-cooled stator bars of the synchronous generator[C]//Proceedings of 2002 International Conference on Power System Technology，October 13－17，2002，Kunming，China.2002:756－760.