改进型Z源并网逆变器

侯世英，黄哲，肖旭，曾鹏，陈剑飞

(1.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆400044;2.重庆电力公司永川供电局，重庆402160)

0 引言

Z源逆变器[1]以其独特的阻抗网络具有可实现直流侧升压变换、允许逆变器桥臂工作于直通状态等优点，因此，无需再控制信号中插入死区时间提高逆变器输出电能质量及系统的稳定性，特别适用于可再生能源发电系统所发出电能的电压低且波动大的特点，具有广阔的应用前景[2－9]。但 Z源逆变器也具有一定的局限性[10]:1)升压因子较小，升压能力十分有限;2)输入电流断续，直流电压利用率低;3)启动初期易造成阻抗网络电感电容谐振，从而造成严重的启动冲击。

针对以上局限性，国内外学者开展了Z源逆变器拓扑优化方面的研究，以致力于完善Z源逆变器的性能。文献[11]提出一种能够减小Z源网络电容电压应力的改进型拓扑，且一定的抑制启动冲击的能力;文献[12]通过改变阻抗网络中无源元件的位置，提出准Z源逆变器，以减小电容电压应力，并减小启动冲击;文献[13]提出了中性点箝位的三电平Z源并网逆变器;文献[14]利用罗氏变换器的思想改进其阻抗网络，提出了具有较高升压比的改进型Z源逆变器;文献[15]提出了双输入双输出的Z源逆变器等。以上文献都能较好的改善Z源逆变器的性能，但其多数只能解决前述分析中指出的1～2种不足，有的甚至以非常复杂的电路结构来换取其性能的提升，不仅增大了电路的体积，也增加了控制系统的复杂程度。

本文在传统的Z源逆变器的基础上，增加1个有源开关及电感，结合传统阻抗网络中的输入二极管在前级构成一个等效Boost电路，以提高拓扑的升压能力;又由于电感的加入，根据电感电流不能突变的特性，在启动过程中限制了启动冲击电流，并且该电感也保证了输入电流的连续。另外，前级的有源开关工作状态与直通状态保持同步，因此无需增加额外的控制电路，尽可能保证了控制系统的简单化。最后，将其应用于单相并网系统中，通过仿真与实验研究，验证了所提出的改进型Z源逆变器拓扑的正确性和有效性。

1 改进型Z源并网逆变器拓扑分析

提出的改进型Z源并网逆变器拓扑如图1所示，其中有源开关 Sb与电感Lb加在传统阻抗网络的前端，与输入二极管在前级构成一个等效 Boost电路，原阻抗网络仍满足对称关系，即:L1=L2=L，C1=C2=C，Z源逆变器有别于传统的逆变器在于其工作状态中存在传统逆变器所严格禁止的直通状态，因此，可将其工作状态等效为直通状态与非直通状态两种，建立其相应的等效电路模型如图2所示。

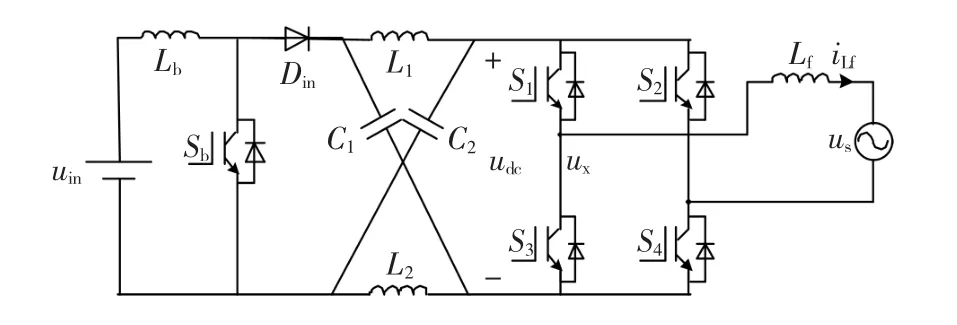
图1 改进型Z源并网逆变器拓扑Fig.1 The topology of improved Z-source grid-connected inverter

图2 改进型Z源逆变器等效电路Fig.2 The equivalent circuit of improved Z-source inverter

当逆变器工作于有效状态以及传统的0状态时，此时逆变桥的输入电流受并网电流控制，因此，逆变桥可用一个电流源等效，其两端电压udc称之为直流链电压，因此，将有效状态与传统的0状态称为非直通状态，等效电路如图2(a)所示。阻抗网络电感L1、L2和电容C1、C2分别具有相同的电感量 L和电容量C，阻抗网络对称，有如下关系，即

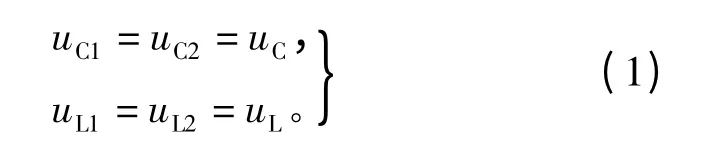
在非直通状态下，开关管Sb关断，二极管Din导通，此时阻抗网络电感L1上的电压为

而前级电感Lb上的电压为

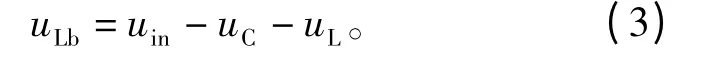
由式(2)、式(3)可得

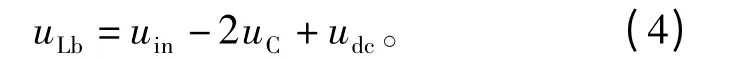
当逆变桥的同一桥臂的两个开关管同时导通的状态称为直通状态，此时逆变桥可用一条短路线等效，直流链电压udc为0，如图2(b)所示。此时闭合开关管Sb，迫使输入二极管Din关断，此时的Z源网络电感L1上的电压为

而前级电感Lb上的电压为

根据电感的伏—秒平衡关系，即在一个开关周期Ts中，电感两端的电压的平均值为0，因此，令直通占空比为D0，那么有效状态的持续时间为(1－D0)Ts，而直通状态的时间为D0Ts，结合式(2)～式(6)，可得改进型Z源并网逆变器的直流链电压udc以及Z源网络电容电压uC与直流侧输入电压uin之间的关系:

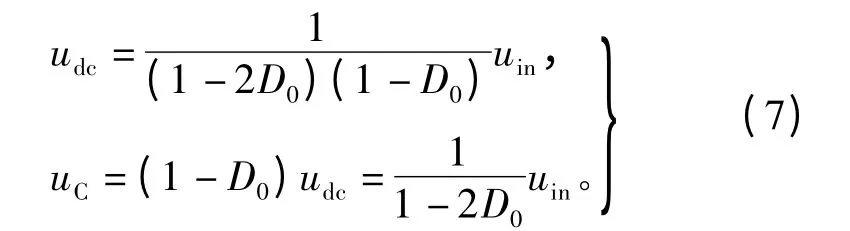
定义改进型Z源并网逆变器的升压因子为B'，那么由上式可得升压因子

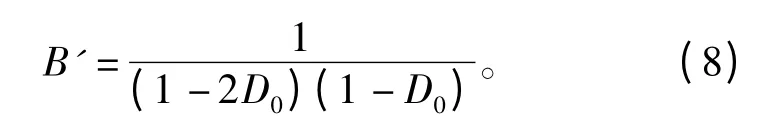
由以上分析可知，改进型Z源逆变器相对于传统的Z源逆变器具有如下优势:

1)提高了升压因子。

文献[1]中给出了传统Z源逆变器的升压因子为B=1/(1－2D0)，结合式(8)得出两种拓扑的升压因子与直通占空比关系对比曲线如图3所示，从图中可知，改进型Z源逆变器相对于传统拓扑在升压能力上有较大提高，而对于相同的网侧电压，改进型拓扑可以将D0控制在较小的范围，以减小逆变器开关管的开关应力，保证良好的输出电能质量。

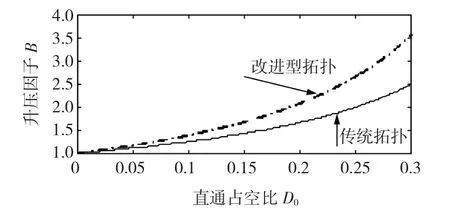
图3 两种拓扑的升压因子B与D0的关系Fig.3 The relationship of B and D0 of these two topologies

2)输入电流连续。

由图2中改进型Z源逆变器在的等效电路模型可知，前级升压电感Lb在直通状态下起到了续流的作用，因此保证了输入电流的连续，提高了直流电压利用率。

3)减小了启动冲击。

传统Z源逆变器在启动初期，阻抗网络电容上的初始电压为0，由于逆变器开关管反并联二极管的作用，会存在如图4(a)所示的通路，造成启动时的输入电流非常大，会将电容电压瞬时充到0.5uin。此后，阻抗网络中的电感和电容开始谐振，可能导致Z源电感电流与电容电压大大超过稳态值，从而造成逆变器损坏。而改进型Z源逆变器的启动回路如图4(b)所示，由于前级电感Lb的存在，在启动过程，根据电感的电流不能突变的特性，限制了启动电流，不会发生迅速将电容电压瞬间充电至0.5uin的情况，因此无需采用软启动策略也不会对逆变器造成影响，简化了启动过程。

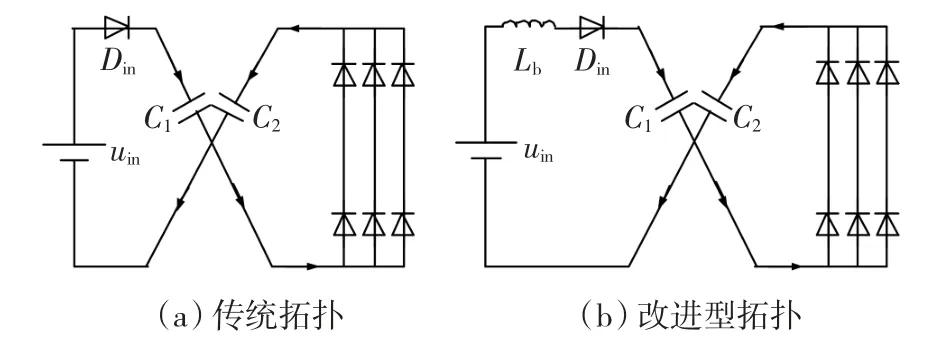
图4 改进型Z源并网逆变器启动时等效电路Fig.4 Equivalent circuit of improved topology when start-up

2 改进型Z源并网逆变器的控制策略

将提出的改进型Z源逆变器应用于单相并网系统中，对其采用电压电流双闭环控制。对于电流控制回路而言，由于并网逆变器的最终控制目标就是将直流电能转换为交流电能并入公共电网，因此，必须对并网电流进行有效控制。根据图1中改进型Z源并网逆变器的拓扑可得并网电流的微分方程的拉氏变换形式为

式中Ux为逆变桥端点输出电压，由于开关频率足够高，阻抗网络工作稳定，则在逆变桥的非直通状态下，直流链电压恒定，根据逆变桥的特性可将其等效为一个惯性环节，于是得到电流环的控制结构如图5所示。

图5 电流环控制结构Fig.5 The block diagram of current control loop

其中:Gi(s)为电流内环调节器的传递函数;Ts为开关周期，考虑到信号的计算、发生、驱动等有半个开关周期的惯性延迟。为了提高电流内环的跟踪速度，通常采用比例环节kp作为调节器传递函数。由此可得电流内环控制系统的开环传递函数

对于电压控制回路而言，需保证稳定的直流链电压udc，但直流链电压中含有直通分量，其本身是一个脉动的方波，此特点给控制系统的设计带来了一定的困难，又由于Z源并网逆变器的直通状态只存在于传统的零状态中，对逆变器的输出并无影响，而真正的有效分量是方波的最大值，由于直流链电压与阻抗网络电容电压存在(1－D0)的关系，通过控制阻抗网络电容电压uC的稳定来间接实现稳定直流链电压的目的。

若忽略变桥交流侧的电阻损耗以及变桥自身的损耗，并考虑逆变器以单位功率因数并网，则变桥并网功率pac应与直流侧有功功率pin相等，即

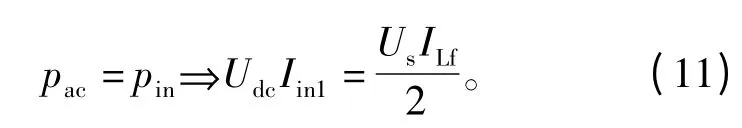
其中:Udc为直流链电压峰值;Iin1为非直通状态下逆变桥的输入电流平均值;Us为网侧电压峰值;ILf为并网电流峰值。由上式整理可得

而对于如图2(a)所示的非直通状态下所对应的电容电流

对于如图2(b)所示的直通状态下，逆变桥的输入电流平均值

直通状态下所对应的电容电流

式中IL为阻抗网络电感电流，由于开关频率远大于系统输出频率，那么在阻抗网络电感足够大时，IL可看作定值。联立式(10)～式(13)，可得改进型Z源网络电容电流的平均值为

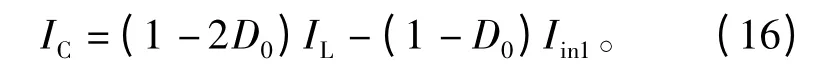
由此可得Z源网络电容电压复频域方程为

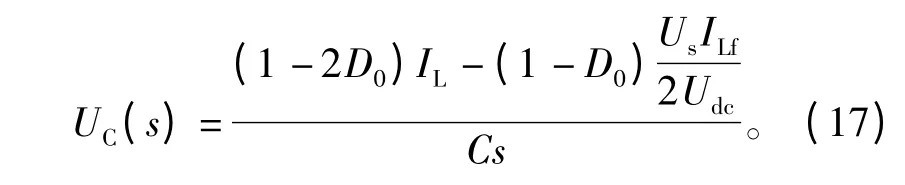
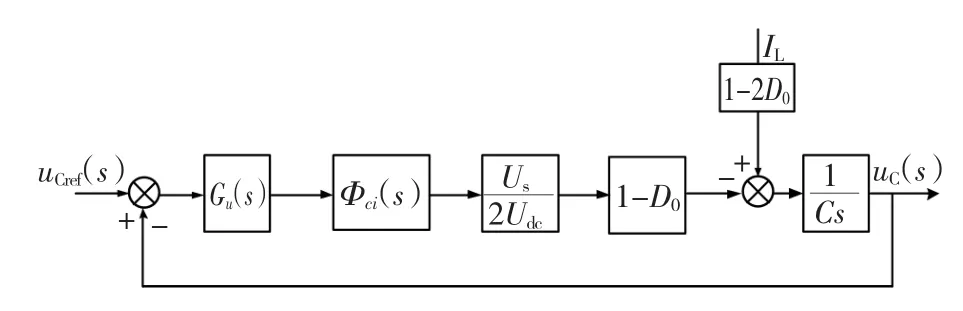
图6 电压外环控制结构Fig.6 The block diagram of voltage control loop

因此，当开关频率足够高且系统稳态时，Z源网络电感电流IL、非直通状态母线电压 Udc、电网电压幅值Us都基本恒定，于是可得出系统的控制结构，如图6所示。

其中Gu(s)为电容电压控制环传递函数，Φci(s)为电流内环的闭环传递函数，由于电流环采用比例调节器，导致电流环输出存在稳态误差，因此为了消除系统的稳态误差，并使系统具有较强的鲁棒性，电压环的调节器选择比例—积分(PI)控制器:

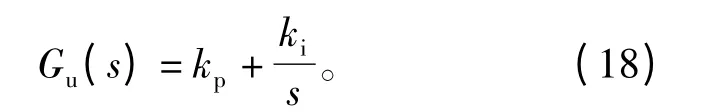
由此可得电压控制器的开环传递函数

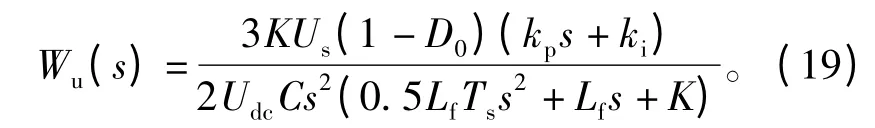
PI调节器的加入相当于在系统中增加一个固定为0的极点外，还可通过调节器的参数选择一个可变零点。通过对零点和增益的改变，可设计符合系统要求的控制器参数。此处PI参数的设计参照经验参数值，然后参照其伯德图及单位阶跃响应进行参数修正，最终得到合理的参数，最终参数下系统的开环伯德图如图7所示，可知系统具有良好的稳定性及动态特性。

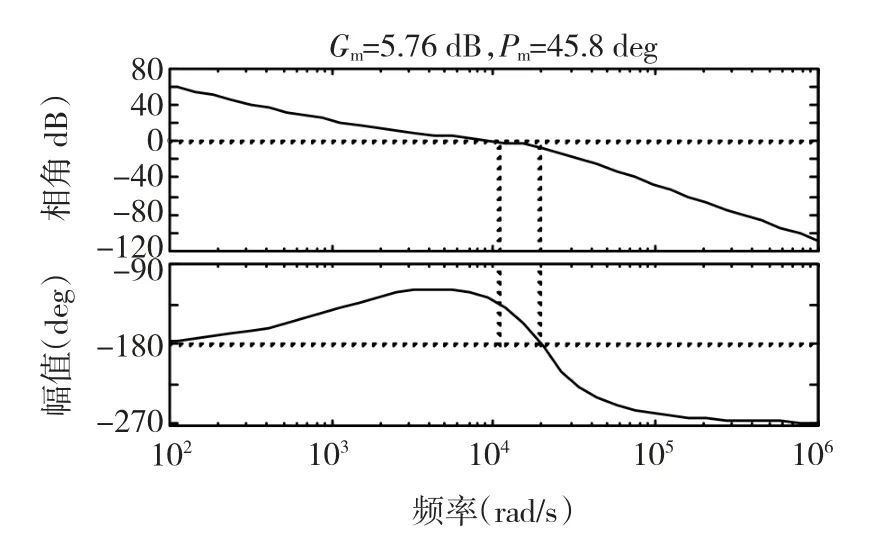
图7 系统的开环伯德图Fig.7 The bode plot of the system

3 仿真验证

基于以上理论分析，对改进型Z源并网逆变器进行了仿真研究。设计了如下仿真参数:网侧为220 V的工频交流电压;直流输入电压uin=300 V;阻抗网络电感 L1=L2=1 mH，阻抗网络电容 C1=C2=1 000 μF;输出滤波电感 Lf=2 mH;载波频率fs=10 kHz;前级电感Lb=2 mH。

仿真结果如图8～图11所示，图8为当设定并网功率为4 kW时，Z源并网逆变器输出波形。从图中可知，并网电流iLf与电网电压 us同频同相，能够按给定的功率以单位功率因数将电能并入电网，并且输出电能质量良好。

图9为直流输入电压uin突变时，Z源并网逆变器输出波形，在0.09 s时，直流电压 uin由300 V突然降为280 V，从图中可知，并网电流iLf几乎不受影响，电容电压在经过0.02 s的小幅波动后随即进入稳态，继续稳定在337.5 V，说明系统具有良好的抗外部干扰能力。

图8 改进型Z源并网逆变器输出波形Fig.8 The output waveform of the improved Z source grid-connected inverter

图9 直流输入电压突变时的输出波形Fig.9 The output waveform of the inverter when the input voltage suddenly changes

图10 为改变并网电流参考信号，使并网功率由4 kW变为4.6 kW时，Z源并网逆变器输出电流波形，从图中可知，并网电流在经过1个工频周期的短暂调节之后达到稳态;其暂态过程中并网电流始终与电网电压保持同频同相，且无超调，由此证明系统具有良好的动态及稳态特性。

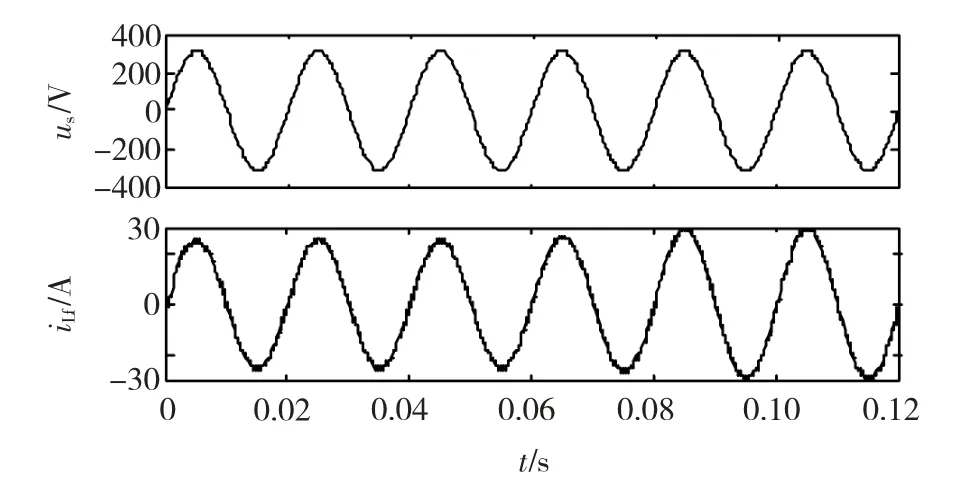
图10 改变参考信号iLref后的电压、电流波形Fig.10 The waveform after changing reference iLref

图11 为在相同的输入电压uin、电容电压uC以及网侧电压us的情况下，传统Z源并网逆变器与改进型Z源并网逆变器的启动过程波形，由此可知无论是从电容电压还是直流链电压来看，改进型拓扑在启动初期的波动明显小于传统拓扑，且快速性较好，在1个工频周期后即可达到稳态;对于阻抗网络电容电压 uC波形，改进型拓扑的超调量仅为3.7%，相对于传统拓扑的36.3%，其启动初期对电容的冲击很小。通过计算可得，当设置阻抗网络电容电压为337.5 V时，改进型拓扑的直通占空比D0为0.056，而传统拓扑D0的为0.1，说明改进型拓扑在升压能力方面有较大的提升。

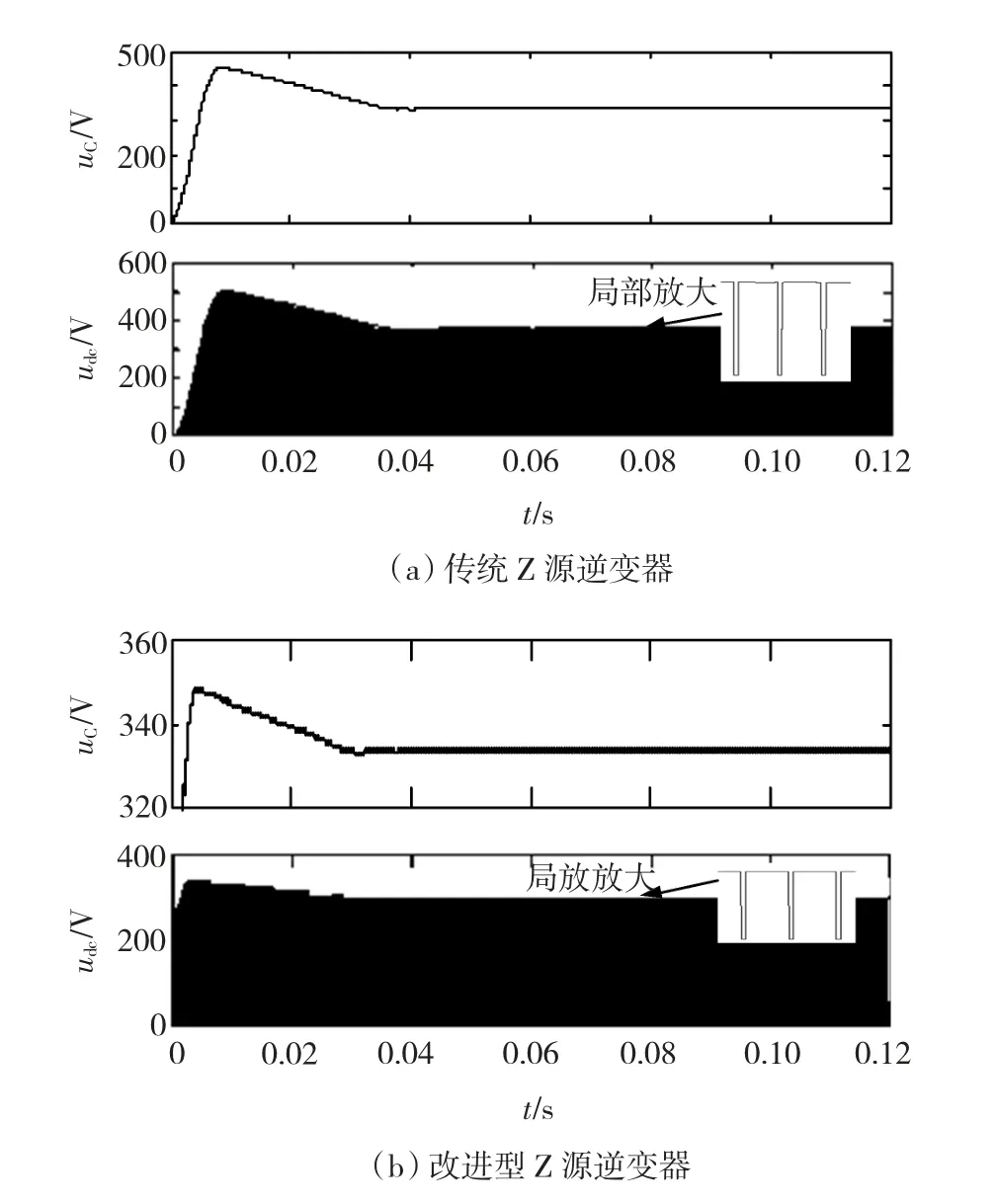
图11 启动过程波形对比Fig.11 The comparison waveform of start process

4 实验验证

为了进一步验证所提出的改进型 Z源并网逆变器的正确性，设计了一台最大输出功率100 W的单相并网逆变系统。其中输入电压70 V，阻抗网络电容1 000 μF，Z源电感5 mH，前级电感8 mH，开关频率为20 kHz，网侧采用60 V/220 V的工频变压器接入电网。

实验结果如图12～图14所示，图12为当输入功率设置为45 W时并网电流iLf与电网电压us的对比波形，由图可知，并网电流iL与电网电压us保持同频同相，并网电流幅值为1 A，通过计算可知系统的效率约为93%，因此，说明该系统具有较高的电能转换率。

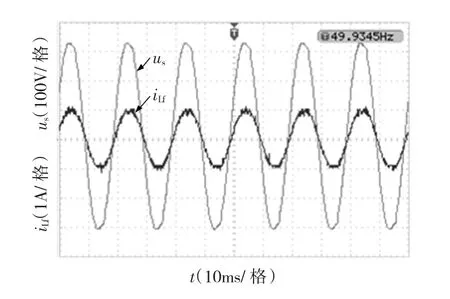
图12 输入功率42 W时的并网电流和电网电压波形Fig.12 The waveforms of output current and grid voltage when the input power is 42 W

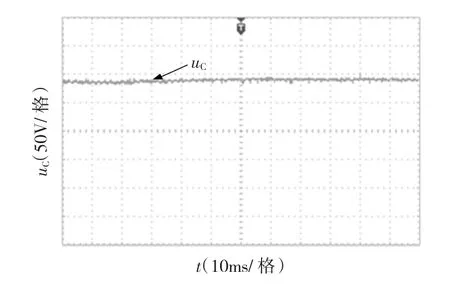
图13 阻抗网络电容电压波形Fig.13 The voltage waveform of Z source capacitor

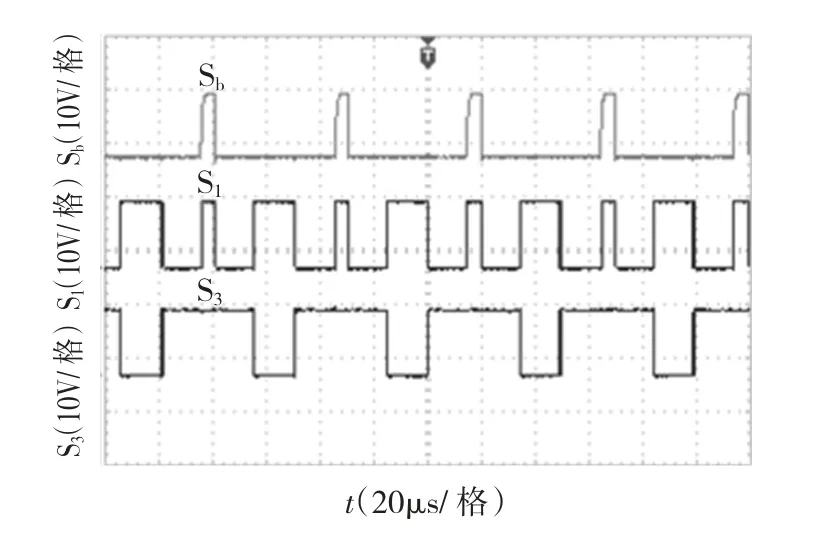
图14 开关管控制信号Fig.14 Control signal of the switch

图13 为阻抗网络电容电压uC波形，由图可知，uC在工作过程中能够保持稳定，其值基本保持在88 V，与式(7)中电容电压与输入电压之间的关系吻合。图14所示为开关管的控制信号，其中自上而下分别为前级开关Sb，逆变桥开关 S1，S3的控制信号，从图中可知，直通脉冲也即为前级开关Sb的控制信号，S1，S3管在直通脉冲出现时同时导通，这为逆变器升压提供了机制。

5 结论

针对Z源逆变器存在的不足，在传统的阻抗网络的基础上，提出一种改进型 Z源并网逆变器拓扑。该拓扑通过增加一个有源开关及电感，与传统阻抗网络中的输入二极管在前级构成一个等效Boost电路，提高了传统Z源逆变器的升压能力，电感的加入也限制了启动冲击电流，并保证了输入电流的连续，提高了直流电压利用率。本文通过仿真与实验验证了该拓扑的可行性。

[1]彭方正，房绪鹏，顾斌.Z源变换器[J].电工技术学报，2004，19(2):47－51.PENG Fangzheng，FANG Xupeng，GU Bin.Z-source converter[J].Transactions of China Electrotechnical Society，2004，19(2):47－51.

[2]侯世英，肖旭，张闯，等.Z源并网逆变器的间接单周电流控制策略[J].电机与控制学报，2011，15(9):18－23.HOU Shiying，XIAO Xu，ZHANG Chuang，et al.The indirect one cycle current control strategy of the Z source grid-connected inverter[J].Electric Machines and Control，2011，15(9):18－23.

[3]PARK Jong-Hyoung，KIM Heung-Geun，NHO Eui-cheol et al.Grid-connected PV System using a quasi-Z-source Inverter[C]//Applied Power Electronics Conference and Exposition，APEC2009，February 15－19，2009，Washington，D.C.USA.2009:925－929.

[4]WELCHKO B A，LIPO T A，JAHNS T M，et al.Fault tolerant three-phase AC motor drive topologies a comparison of features，cost and limitations[J].IEEE Transactions on Power Electronics，2004，19(4):1108 －1116.

[5]Gajanayake C J，Vilathgamuwa D M，Poh C L.Modeling and design of multi-loop closed loop controller for Z-source inverter for Distributed Generation[C]//IEEE Power Electronics Specialists Conference，South Korea，2006.

[6]付胜杰，彭侠夫.六相逆变器空间矢量脉宽调制策略的分析与优化[J].哈尔滨工程大学学报，2012，33(4):512 －516.FU Shengjie，PENG Xiafu.Analysis and optimiazation of SVPWM strategy for a six-phase inverter[J].Journal of Harbin Engineering University，2012，33(4):512 －516.

[7]Holland K，Peng F Z.Control strategy for fuel cell vehicle traction drive systems using the Z-source inverter[C]//Proceedings of IEEE Vehicle Power and Propulsion Conference，Sept 7 － 9.2005，East Lansing，USA.2005:639－944.

[8]张敬南，丛望.船舶电力推进六相同步电动机控制研究[J].哈尔滨工程大学学报，2010，31(9):1209－1216.ZHANG Jinnan，CONG Wang.Controller for a six-phase synchronous motor used for marine electrical propulsion[J].Journal of Harbin Engineering University，2010，31(9):1209 －1216.

[9]TANG Yu，XIE Shaojun，ZHANG Chaohua.An improved Z-source inverter[J].IEEE Transactions on Power Electronics，2011，26(12):3865－3868.

[10]汤雨，谢少军，张超华，改进型 Z源逆变器[J].中国电机工程学报，2009，29(30):28 －34.TANG Yu，XIE Shaojun，ZHANG Chaohua.Improved Z-source[]，，():

[11]P.C.Loh，F.Gao，F.Blaabjerg.Topological and modulation design of three-level Z-source inverters[J].IEEE Transactions on Power Electronics，2008，23(5):2268 － 2277.

[12]DmitriVinnikov，IndrekRoasto，RsyzardStrzelecki，MarekAdamowicz.Step-up DC/DC Converter with Cascaded Quasi-Z-Source Network[J].IEEE Transactions on Industrial Electronics，2012，59(10):3727－3736.

[13]LOH P C，LIM S W，Gao F，et al.Three-level Z-source inverters using a single LC impedance network[J].IEEE Transactions，，():

[14]ZHU Miao，YU Kun，LUO Fanglin.Switched-inductor Z-source inverter[J].IEEE Transactions on Power Electronics，2010，25(8):2150－2158.

[15]DEHGHAN S M，MOHAMADIAN M，YAZDIAN A.Dual-input dual-output Z-source inverter[C]//IEEE Energy Conversion Congress and Exposition(ECCE)，California，USA.2009:3668－3674.