用时最短问题求解五法

张新华

(浙江省天台中学 浙江 台州 317200)

一艘渔艇停泊在距岸9 km处，今需派人送信给距渔艇15 km处的海岸渔站，如果送信人步行每小时5 km，船速每小时4 km,问应该在何处登岸，再步行可以使抵达渔站的时间最省？

解法一：矢量分解法

不妨先设人从岸上出发，再跳入水中到达船原来所在的位置，该过程所花的时间与坐船沿相同路径到岸边再跑至渔站所花的时间相等．

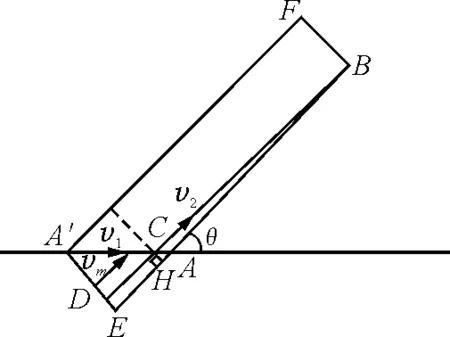
如图1，A为渔站，B为渔艇原来的位置，AB与岸方向夹角为θ．

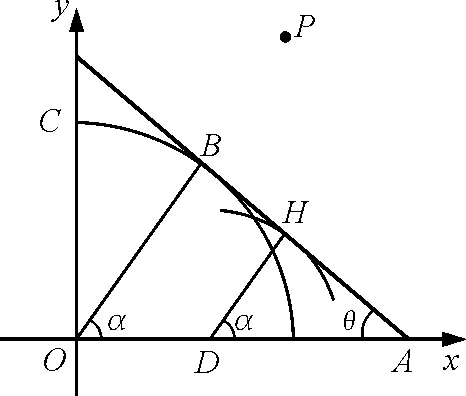
图1

设人在岸上先经C点，再进入水中．

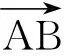
tAC=tEC

(1)

又

故直接从A到B，在AH段所花时间与从E到C(即A到C的分运动)所花时间相等．所以

tAH=tEC

(2)

由式(1)、(2)可知

tAC=tAH

(3)

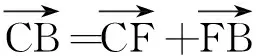
人从C到B所用时间等于从C到F所用时间，即

tCB=tCF

(4)

所以tHB

(5)

由式(4)、(5)可知

tHB

(6)

综上所述

tAHB=tAH+tHB

所以，在本题中选A→H→B的路线(即直航路线)最合适．

有同学会认为本题中直航的走法具有偶然性．若渔站在A点左侧A′点(如图2)，应当怎么走呢？

图2

答案是先从A′点走到A点，再在A点下水直达B，此时A点是与B连线与岸夹角为θ的点

下面给出证明：

情况一：人过A点后继续跑，直到C点才下水．那么人在后半段，即A→C→B所花的时间将大于从A直接到B所花的时间．

tA′A=tEA

(7)

若人在C点下水，则其轨迹为A′→C→B，且

tA′C=tD C=tEH

(8)

而由图可知CB>HB，又因为人在CB段的速度为

v2=4 m/s

在HA段及AB段(即为HB段)的速度也为4 m/s．

所以tCB>tHB

(9)

由式(7)～(9)可知

tA′CB=tA′C+tCB=tEH+tCB>

tEH+tHB=tEA+tAB=tA′A+tAB=tA′AB

综上可得：结论是tA′AB为最短时间．

解法二：边界法

如图3，以岸为x轴，渔站为O点，建立坐标系．

图3

设经时间Δt，作一以OC=v2Δt为半径的圆，这是不跑，直接进入水中的一种状态．再在x轴上作一直线长为OA=v1Δt,这是不跳水，只跑的状态，两个状态均用掉Δt时间．

过A作圆O的切线交于B点，设AB与x轴负方向夹角为θ．

设经时间Δt′(Δt′<Δt)后跳水，则在岸上行OD=v1Δt′，作DH⊥AB，且交AB于H点.则

所以

DH=v2(Δt-Δt′)

而这即是在岸上用掉时间Δt′后，在水中所能游的最大半径．

又因为该半径与直线AB垂直，故圆D与AB相切．因为D是任意点，故对所有的0≤Δt′≤Δt，上述结果均成立，故AB是无数个圆组成的包络线．

而CBA与x轴、y轴围成的区域即为Δt内可能到达的最大范围．

又因为CBA是界限，而到达界限是一个临界状态，即冲在最前头．

而到达界限所选择的路径恰巧是先在岸上走，再垂直于边界游，直至到达到目的地．此时所花时间最短(单位时间内能游到最远处)，而此时在水中游的速度方向与x轴的夹角α满足

由题意，渔站与渔艇的连线与x轴恰好成α，故直通最省时．

解法三：类比法

由费马原理可知：光沿光程为极值的路径传播．若人所选择的路线最省时，不妨将人类比为光．

设人在岸上走的速率为v1，在水中的速率为v2．

图4

如图4，根据光的折射定律得

所以人进入水后的速度方向与岸的夹角为

即直通最省时．

解法四：求导法

如图4，设AC=x,则CD=12-x.

在直角△BCD中

则

故总时间

上式中t对x求导后，令t′=0,解得x=0.

故在A处登岸最合适．

解法五：微元法

图5

如图5，设A→E→B为最合适的路径．

在E的右边取一点C，令EC=Δx且Δx→0

由数学知识可知，tAEB为总时间t是关于x(x=AE)的一个极值．

在极值处，t的导数值为零，故在该处附近，t关于x的变化率为零，即Δt→0.

故人沿ACB行走所花的时间与沿AEB行走所花时间之差Δt=0.

而人从E→C代表在岸上多跑了时间

在水中(C→B)少花的时间可近似为

因

Δt=tEC-tEH=0

故可解得

由题意，直通最合适．

因时间t关于x(x=AE)的函数极值附近有左极限和右极限，以上只证明了其中一个．

对于另一种的讨论，请读者参照图6自行证明，本文不再赘述．

图6

点评：

一道题目，五种解法，殊途同归，各有千秋．

方法一浅显易懂、思维严密，是解决此类问题的“通法”，是重要的物理模型；

方法二受“惠更斯原理”启发，知识覆盖面广，应用灵活；

方法三思路清晰，运算量少，体现了类比的思想方法；

方法四体现了导数强有力的“工具性”，也是一种十分可取的方法；

方法五体现了微元的思想，与方法四原理类似，但运算量大大减小．

由此可见，本题的五种解法对培养学生发散性的思维能力，强化对知识的应用能力都大有裨益．