浅谈变换参考系在能量问题中的应用
姜荣
(江苏省海门中学 江苏 南通 226100)
在处理涉及运动类的问题和牛顿运动定律的问题时,可以通过参考系的变换简化问题的解决,实际上,在处理涉及能量的许多问题时,如果通过参考系的变换,同样也可以起到意想不到的效果.
1 推导变换参考系后的动能定理表达式
【例1】如图1所示,一辆小车以速度v1匀速前进,一人站在车内手持一质量为m的小球,现在人将手中的球沿车内平面推出,相对人前进s2.已知该球离开手时对地速度为v2,推球过程车前进s1,为简化该问题的研究,把人将小球推离的过程中对小球的作用力F视为一恒力来推导动能定理表达式.
解析:(1)选地面作为参考系
人在推离小球的过程中所做的功为
W1=F(s1+s2)
小球动能变化
根据动能定理可得
W1=ΔEk
即
(1)
(2)以小车作为参考系
人在推离小球的过程中所做的功为
W2=Fs2
(2)
小球动能变化
(3)
设人推离小球的过程中作用时间为t,那么对小球利用动量定理可得
Ft=m(v2-v1)
所以
Fv1t=mv1(v2-v1)
即Fs1=mv1(v2-v1)
(4)
将式(4)代入式(3),同时结合式(1)和式(2)可得
由此可见变换参考系后动能定理的表达形式还是一样的,只需将所涉及的物理量以新的参考系变换一下即可.
我们对该问题做进一步研究,笔者曾问过学生人在将小球推出的过程中消耗了多少化学能?学生提供了两种解法.
解法一:选地面为参考系,根据功能关系
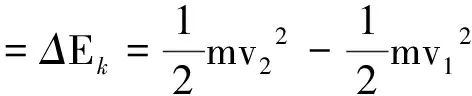
解法二:选小车为参考系,根据功能关系
显然这两种解法所对应的最终值是不一样的,但是消耗的能量无论选择哪个参考系都应该是一样的,那么到底哪种解法正确呢?
为了解决这一问题,我们先回到地面参考系中,人在推出小球的过程中对小球施加了一个向右的力F,与此同时,球也给人一个向左的力F.由于人所受的合外力为零,所以地板给人一个向右的摩擦力,大小也为F,此力给人和小球组成的系统做的功为Fs1,此功消耗的能量是小车提供的,不是人提供的,故选小车作为参考系时,人所消耗的能量应为以地面为参考系,人和小球系统机械能的增量减去小车提供的能量,即

(5)
根据前面的分析可得Fs1=mv1(v2-v1),代入式(5),可得

这与选择小车作为参考系的结果是一样的,由此可以看出无论选择地面还是小车作为参考系所消耗的能量是一样的,只不过消耗能量的解法一没有考虑到人对球做功的同时,车也在对人和小球组成的系统做功,所以解法一是错误的.
2 通过变换参考系简化问题研究
2.1 变换参考系思想在惯性系中的应用
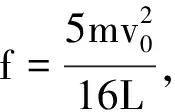

图2
解析:设子弹射出时相对地面的速度为v,选木块作为参考系,由动能定理,对子弹
(6)

(7)
如果该题选择地面为参考系,也可以得到同样结果,只是过程显得繁琐一些,读者可尝试解决.
2.2 变换参考系思想在非惯性系中的应用
【例3】(第27届全国中学生物理竞赛预赛第8题)如果在地球表面纬度为φ处发射一颗绕地球表面运行的人造卫星,假设地球可视为质量均匀分布的球体,已知地球自转的角速度为ω,地球半径为R,地球表面处的重力加速度为g,卫星的质量为m,则至少要给卫星的能量为多大?
解析:由例1分析可知此题如果选地心为参考系,需要考虑旋转的地球做的功,这样,显得比较繁琐.为简化该问题的解决,可以选择地面为参考系,地面参考系为非惯性参考系(由于地球的质量远大于卫星的质量,故可以认为发射卫星的过程中地球的自转角速度不变),且卫星相对地面还有相对运动,所以计算时还需考虑惯性离心力和科里奥利力所做的功.为了减少能量的消耗,卫星应由西向东发射(与地球自转方向相同),经判断,发射过程中惯性离心力和科里奥利力均与速度垂直,故此两力不做功,因此至少要给卫星的能量为
通过对例1的讨论,可以看出选择不同的参考系,可以得到相同的结果,但是对该问题的进一步探究,可以发掘出不同参考系背后深层次的物理本质,从而加深对物理学习的理解.对例2和例3,选用适当的参考系,可简化问题的计算,这也给我们带来很大的启发,即解决涉及能量的许多问题时,可以从变换参考系的角度思考,简化问题的解决.

