狭义相对论中事件概念的教学*①

张登玉 游开明 高 峰 王友文

(衡阳师范学院物理与电子信息科学系 湖南 衡阳 421002)

1 引言

经典力学认为时空和质量的测量有绝对意义，与观测者所处的参照系无关，这种绝对时空和绝对质量观念的集中反映便是伽利略变换．但从19世纪后期起，一些物理学家逐渐发现这种观念和高速运动的实验事实不符．从目前的史料看，爱因斯坦在建立相对论时深受马赫的影响，他似乎对洛伦兹和庞加莱的工作知之不多．爱因斯坦多次谈到马赫对自己的影响．正是马赫提出的“一切运动都是相对的”，根本不存在“绝对空间”和“绝对运动”的论述，以及其对“以太”是否存在的质疑( 他认为没有任何实验证明存在“以太”) ，使爱因斯坦坚信“相对性原理”是必须坚持的一条根本原理，是科学的一条“真理”，而以太理论是可以放弃的．爱因斯坦创立的狭义相对论同经典物理学相比较, 最显著的特征是: 建立了新的时空概念, 揭露了质量和能量的内在联系, 量度物体运动的“钟” 、“尺” 和物体的质量不再是绝对不变的, 而当它们相对于观察者运动时, 具有“钟变慢”、“尺变短”、质速关系和质能关系等相对性效应．狭义相对论两个基本原理是：

(1)相对性原理——物理定律在所有惯性系都有相同的形式；

(2)光速不变原理——真空中的光速在所有惯性系沿任何方向都是常量c，与光源的运动无关．

狭义相对论中最基本也是非常重要的概念是事件．事件是从物质运动中抽象出来的，物质运动可以看成是一连串事件的发展过程，事件有各种不同的具体内容，但是它总是在一定地点和一定时刻发生的，因此可以用四个坐标(x,y,z,t)代表一个事件．事件概念可看作是一个理想模型．由于事件在间隔不变性、洛伦兹变换和相对论的时空理论(时空结构、因果律、同时相对性、运动时钟的延缓、运动尺寸的缩短、速度变换公式)均有重要的应用，因此在狭义相对论教学中必须引起高度重视．

2 事件概念与间隔不变性和洛伦兹变换

惯性系Σ上两个事件可表示为(x1,y1,z1,t1), (x2,y2,z2,t2),其间隔为

s2=c2(t2-t1)2-(x2-x1)2-

(y2-y1)2-(z2-z1)2

(1)

(2)

由间隔不变性有s2=s′2．间隔是将时间和空间距离统一起来的一个概念．

假定同一事件在惯性坐标系Σ用(x,y,z,t)表示，在另一惯性坐标系Σ′用(x′,y′,z′,t′)表示，选Σ坐标系的x轴和Σ′坐标系的x′轴都沿Σ′相对于Σ的运动方向，Σ′相对于Σ的运动速度v．则同一事件时空坐标满足变换

y′=yz′=z

(3)

变换式(3)称为洛伦兹变换式．这是同一事件在两惯性系中时空坐标间的变换关系，应用此式时应先确定事件在Σ坐标系的坐标，再利用(3)式求出该事件在Σ′坐标系中的坐标．

3 事件概念与运动时钟延缓和运动尺度缩短

(4)

Δτ为该物体的静止坐标系测出的时间，称为该物理过程的固有时间，由于Δt>Δτ，表示运动物体上发生的自然过程比起静止物体的同样过程延缓了．

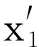
(5)

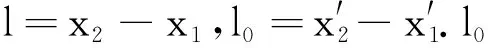
4 实例

【例题】静止μ子的平均寿命是2.2×10-6s，在实验室中，从高能加速器出来的μ子以0.6c(c为真空中光速)运动．问：

(1)在实验室中观测，这些μ子的平均寿命是多少？它们在衰变前飞行的平均距离是多少？

(2)相对于μ子静止的观测者观测到它们衰变前飞行的平均距离是多少？

解：(1)在与μ子相对静止的参照系观察到μ的平均寿命2.2×10-6s为物理过程的固有时，在实验室参照系观测其寿命为

上式表明运动物体上发生的自然物理过程比起静止物体的同样过程延缓了．

在实验室参照系观测μ子衰变前飞行的平均距离

l=vΔt=4.95×102m

(2)相对μ子静止的观测者观测到μ子飞行的平均距离为

即运动尺度缩短了．

5 结论

在洛伦兹变换和相对论时空理论中，应加强和突出事件概念的教学，搞清所研究的问题涉及的是一个事件还是两个事件以及具体的事件在Σ坐标系(参照系)的坐标还是Σ′坐标系的坐标，从而更好地理解固有时间和固有长度等概念，再准确利用有关公式进行计算．

参考文献

1 郭硕鸿.电动力学.北京：高等教育出版社，2008

2 唐福忠，唐皓颖，范佳午.浅谈狭义相对论中的观测与观看.物理教师，2007,28(4):38～39

3 康颖.大学物理(下册).北京：科学出版社，2010