“太阳与行星间的引力”教学的创新

陈伟锋

(北京师范大学物理系 北京 100875；宁波效实中学 浙江 宁波 315012)

“太阳与行星间的引力”是新课程中新增的内容，对于培养学生的探究精神与掌握一种科学探究方法很有好处.

探究太阳与行星间的引力是万有引力定律发现过程中的关键一步，离万有引力定律的最终确立，不仅有时间上的差距，更重要的是思想上存在的差距.所以，教材设置这节教学内容符合建立万有引力定律的时间顺序和人们进行科学探索时从个别到一般的逻辑顺序[1,2].

1 教学的两个关键点

教材根据开普勒行星运动定律和牛顿运动定律得出太阳与行星间的引力，是已知运动求力的理论探究过程.在探究引力与太阳的质量的关系时，大胆地假设了太阳与行星的“地位是相同的”.这一假设很好地说明了物理学的研究需要在观察和实验的基础上进行此类猜想和思考.所以，这节内容是很好的科学探究教育和思想方法教育素材，从教学目标的三个维度来看，过程与方法、情感态度与价值观应重于知识与技能.基于上述认识，本课的教学应把握好两个关键之处：

一是应突出“已知行星运动求引力”的科学探究方法的教学，可以根据学生已有的知识构建一个“类行星运动模型”，为学生独立探究太阳与行星间的引力设置好台阶；

二是应充分挖掘“然而，从太阳与行星间的相互作用的角度来看，两者的地位是相同的”这句话的教育价值.

2 以“类行星运动模型”为台阶探究引力

开普勒行星运动定律总结了行星运动的轨迹、绕日运动的快慢、绕日转动的快慢，停留在对行星运动的描述阶段.牛顿把他的动力学观点推广到了太阳系，从动力学角度研究行星的运动，把它看做是已知运动(开普勒行星运动定律)求力的问题.把椭圆轨道近似为圆轨道后，问题就被简化了：行星做匀速圆周运动，太阳对行星的引力提供向心力.虽然，简化后的问题属于前一章的知识范畴，但是让学生独立地探究太阳与行星间的引力还是有难度的.为帮助学生登上探究引力的“高山”，教师可以想办法设置登山的“台阶”，凭借学生熟悉的情境和圆周运动知识，构建出一个与行星运动“类似的”匀速圆周运动系统，不妨把它叫做“类行星运动模型”.通过研究“类行星运动模型”中的动力学关系，启发学生思考，为学生独立地探究太阳与行星间的引力创造条件.

如图1所示，质量分别为m1，m2，m3的三个小球正在高度不同的光滑水平面上做匀速圆周运动.已知连接小球用的轻弹簧完全相同，弹簧的固定端O1,O2,O3在同一竖直线上.它们的运动与行星的运动有相似之处，你能仿照开普勒行星运动定律，得出它们运动的第一定律和第二定律吗？三个小球做圆周运动的半径r的三次方跟它们的周期T的二次方的比值都相等吗？

图1

在这个匀速圆周运动系统中，小球做匀速圆周运动的向心力是弹簧弹力，遵守胡克定律F=κx，是学生已知的力.而三个小球运动的周期规律是未知的.所以，这是一个已知“力”求“运动”的问题，是一个与探究太阳与行星间的引力“相反的”探究过程.第一定律和第二定律可以让学生通过分组讨论得出.

(1)小球运动第一定律——所有小球运动的轨迹是圆；

(2)小球运动第二定律——所有小球都做匀速圆周运动；

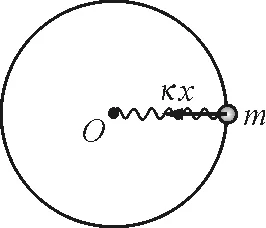
图2

(3)小球运动第三定律可由师生一起探究得出，也是为学生独立地探究太阳对行星的引力做准备.如图2所示，研究任意一个小球.小球做匀速圆周运动，弹簧弹力提供向心力，根据牛顿运动定律有

(1)

把式(1)整理成与开普勒第三定律相同的形式，即

(2)

则式(1)左边写成未知力F后，为

(3)

联立式(2)、(3)，可得

F=κx

最终揭示“类行星运动模型”中的动力学关系——周期规律,即

式中隐藏着胡克定律F=κx；从而使学生联想到要寻找的引力隐藏在开普勒行星运动第三定律的背后.

师生通过共同探究“类行星运动模型”中的运动和力的关系，复习了匀速圆周运动的动力学知识，揭示了开普勒行星运动的深层次含义，加深了学生对动力学观点的理解.在此基础上，让学生通过独立探究得出太阳对行星的引力的初步表达式

是完全可行的.从该式进一步得出引力的最后的表达式

则需把握好第二个关键点.

3 意味深长的“假设”

教材在进一步推导引力的大小也应与太阳的质量成正比时，是这样编写的：“然而，从太阳与行星间的相互作用的角度来看，两者的地位是相同的.”[1]我们知道 “地位相同”不是物理定律或实验事实，而是一个大胆的“假设”.这在物理学研究中是必不可少的.那么，这里究竟包含了哪些假定因素呢？按照教材的思路，答案显而易见:在得到引力与行星质量成正比的前提下，假设太阳质量也以同样的正比关系影响引力.在没有实验事实和理论依据的情况下提出这一假设的依据只能是出于直觉，一种以一定的哲学信念为背景的直觉.基于这一假设，使得太阳与行星间引力表达式有了简明美丽的特点，而这正是物理学所追求的.

参考文献

1 人民教育出版社，课程教材研究所，等.普通高中课程标准实验教科书物理·必修2.北京:人民教育出版社，2010

2 漆安慎,杜婵英.力学. 北京:高等教育出版社，1998