地震荷载作用下桩承式加筋路堤动力响应分析

赵建斌， 龙 凡， 郑俊杰

(1. 山西省交通科学研究院 黄土地区公路建设与养护技术交通行业重点实验室， 山西 太原 030006；2. 浙江大学 建筑工程学院， 浙江 杭州 310058；3. 华中科技大学 土木工程与力学学院， 湖北 武汉 430074)

桩承式加筋路堤通过砂石垫层、水平加筋体、桩和地基土共同作用，工作性状十分复杂。国内外对其进行了深入研究[1～3]。但是，上述研究都是集中于对桩承式加筋路堤作用机理、筋材的变形和力学特性、桩的变形与力学特性等的静力分析。目前，对桩承式加筋路堤的的动力分析甚少[4]，刘飞禹建立了三维动力流固耦模型，分析了交通荷载下桩承式加筋路堤的动力特性[5，6]。而国内外关于路堤在地震作用下的记录资料几乎是空白[7～9]。袁捷采用Biot动力固结理论分析了在地震荷载作用下，加筋土路基的力学行为[10]；陈育民利用FLIP程序分析了堤基及上部堤防地震液化变形的规律[11]；王建在对汶川地震震区路基震害进行调查的基础上，对土工格栅加筋路堤加固效果进行了动力分析[12]。针对地震作用下桩承式加筋路堤动力响应方面研究的不足，本文对水平地震波El-Centro作用下桩承式加筋路堤动力响应进行了分析，并运用控制变量法，对格栅模量和桩间距进行了参数分析，得出了一些有意义的结论。

1 数值模型

1.1 数值分析模型

本文基于某桩承式加筋路堤工况，采用有限差分软件FLAC建立了数值模拟动力模型。试验段路堤路面宽13.2 m，填土高度3.5 m，坡比1.17∶1。为了减少边界效应对模型结果的影响，取边界到坡脚的距离为19.2 m。模型厚度18.0 m，长度38.4 m，考虑到该路堤为平面应变问题，纵向取1.6 m，共划分1804个网格。在平衡地应力静力计算部分，边界条件取天然状态下计算边界条件，根据模型的平面应变条件，取模型的底面为固定边界，前后左右面边界均只约束水平方向位移。在动力分析中，为了避免向外传播的地震波在边界上反射到模型内部从而不能使能量有效地消耗，故采用静态边界或自由场边界来有效地吸收向外传播的地震波并且不显著增加计算量。在此有限差分模型中，底部边界采用静态边界，四周采用自由场边界。另外模型为平面应变问题，故所有节点都不允许在平面应变方向移动。计算模型如图1。

图1 计算模型

1.2 材料参数

试验段土层的物理力学参数如表1所示。数值分析模型中土体采用理想弹塑性本构模型，屈服准则采用Mohr-Coulomb强度准则。

该试验段地基处理方案采用的是13根CFG桩和单层格栅，采用的CFG桩桩长5.0 m，桩径0.5 m，桩距1.6 m，弹性模量10 GPa，单桩承载力设计值不小于590 kN；经编双向土工格栅抗拉模量为0.5 GPa，其抗拉强度不小于250 kN/m。桩和格栅分别采用FLAC中内置桩单元和格栅单元进行模拟。

表1 土体物理力学参数

1.3 地震荷载的输入

在施加地震荷载作用的动力计算部分，模型底部设置静边界，而为了吸收地震过程中地震波在边界上的反射，在模型四周设置了自由场边界，设置自由场边界后，程序会自动在模型的四周生成一圈自由场网络，通过自由场网格和主体网格的耦合作用来近似模拟自由场地震动的情况。在模型底部输入El-Centro地震波加速度时程，持续时间10 s，El-Centro地震波加速度峰值为0.1g，加速度时程曲线如图2。

1.4 监测点的布置

在计算中对图1中路堤中线(AB线)和右坡面(CDE线)进行监测，监测的动力响应包括加速度、动位移和动应力等。同时对土工格栅和13根CFG桩也进行了位移和内力的监测。

2 桩承式加筋路堤动力特性研究

2.1 路堤模型变形破坏模式

水平输入El-Centro地震波，作用10 s后，变形后的网格如图3所示，剪切应变增量云图如图4所示。路堤填土在水平地震作用后，路堤路面左边向下沉降，右边路面隆起，产生了一定的不均匀沉降；而路堤填土与路基土体产生循环挤压和拉伸作用，在路堤坡脚处由于应力集中效应，使得路堤坡面下部出现鼓胀破坏，坡脚底部地面隆起；从剪切应变增量云图上看，最大剪切应变增量在路堤右坡面坡脚上方0.7 m附近。

图3 变形前后模型网格图(放大系数50)

图4 右坡面剪切应变增量云图

2.2 加速度峰值放大系数

震害调查表明，与加速度有关的地震惯性力是场地产生变形和失稳的主要原因，因此模型的加速度反应及其分布规律等，是评价模型地震动力响应性状的基本资料，其中放大系数即某一点输出加速度峰值与输入地震荷载峰值之比。图5中桩承式加筋路堤右坡面(CDE线)加速度峰值放大系数是随高程的增加而增加、下降、再增加的过程。路堤对地震动的反应强度存在两个重要影响因素：入射波与反射波叠加形成的临空面放大效应和岩土材料阻尼对入射波吸收所造成的衰减效应。在路堤底面B点，水平加速度基本没有放大或衰减，加速度峰值放大系数接近1，随着高程的增加，临空面放大效应占据主导因素，从而加速度峰值放大系数会随高程增加而增大，即第1上升段；而当高程增加大约10 m时，在CFG桩加固区，入射波经过吸收后，其阻尼衰减效应超过临空面放大效应而占据了主导因素，加速度表现为沿程增高而衰减，即衰减段；距坡顶一定距离时，由于增加了路面这个临空面，使得入射波和反射波多次叠加，临空面放大效应又超过阻尼衰减效应而占据优势，从而加速度表现为沿高程增加而再次放大，即第2上升段。

图5 右坡面加速度峰值放大系数

2.3 动剪应力峰值

图6为监测的路堤右坡面(CDE线)上动剪应力峰值分布曲线，在到范围内动剪应力峰值基本不变，维持在32 kPa左右；随着高程地增加，在CFG桩加固区，由于CFG桩的加固作用，动剪应力峰值有一个下降的过程；在路堤右坡面，动剪应力峰值在坡脚上方0.7 m处左右达到最大值，从剪切应变增量云图可以看到此处路堤剪切应变增量也达到最大值。

图6 右坡面动剪应力峰值分布曲线

2.4 水平动位移峰值

图7为路堤右坡面(CDE线)上水平动位移峰值变化曲线。水平动位移峰值随着高程的增加而先增加；在路堤填土坡脚处，由于路堤填土刚度和质量都小于下层的CFG桩加固区，因而动位移峰值在坡脚处有一个陡增；在坡脚上方0.7 m处左右达到最大值8.4 cm后，水平动位移峰值开始随着高程的增加而降低。

图7 右坡面动位移峰值分布曲线

2.5 位移时程曲线

在路堤中线(AB线)上，监测了z方向坐标分别为3.5 m、0 m、-4.5 m和-14.5 m四点的位移时程曲线。路堤顶部(z=3.5 m)位移峰值最大；z=0 m处位移时程曲线峰值与路堤顶部位移峰值很接近，且相位差很小；路堤底部(z=-14.5 m)位移峰值最小，与z=-4.5 m处的位移时程曲线相比，相位差较大，位移峰值相差也比较大，说明在z=-14.5 m到z=-4.5 m范围内的土体产生了较大的剪切变形，在动剪应力峰值分布曲线图中可以看到，这个范围内动剪应力峰值维持在比较高的水平，这可能导致了较大的剪切变形。

图8 AB监测线上位移时程曲线

2.6 土工格栅和桩的内力

图9和图10分别为水平地震作用下桩承式加筋路堤土工格栅拉应力增量峰值和桩身剪力增量峰值的分布图。图中可以看到在水平地震作用下，土工格栅的拉应力峰值最大值出现在x=-6 m和x=6 m附近，在中间和两端峰值较小；CFG桩身动剪力峰值最大值是第2跟和第12跟，除了两端的两根桩承担较小的动剪力，越靠近中间的桩，桩身剪力峰值越小，且各桩最大动剪力皆发生在靠近桩顶部分。说明桩承式加筋路堤中土工格栅的主要是承担桩间土上部的荷载，将竖向荷载通过土工格栅的拉力转移到作用在桩顶的竖向荷载，从而通过桩侧摩阻力和桩端阻力将上部荷载传递到深层土体。在水平地震作用下，由于路堤填土与路基土体反复循环的挤压与拉伸作用，路堤填土靠近中线的地方，土体的应变要比路肩附近小。

图9 土工格栅拉应力峰值分布曲线

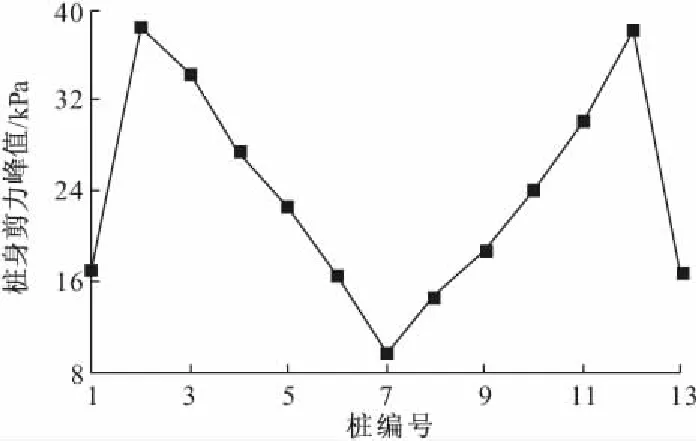
图10 桩身剪力峰值分布曲线

3 参数分析

3.1 土工格栅模量

分别对土工格栅模量为0.2 GPa、0.5 GPa、0.8 GPa和1.2 GPa的桩承式加筋路堤进行了动力分析。在图11中可以看到，增大土工格栅模量，能减少路堤右坡面水平动位移峰值，格栅模量为1.2 GPa时在最大水平动位移峰值处比格栅模量为0.2 GPa时可减少1.4%。

图12为不同的土工格栅模量下，路堤路面中点A点的竖向动位移峰值，从图中可以看到，土工格栅模量越大，A点的竖向动位移峰值越小，格栅模量为1.2 GPa时比格栅模量为0.2 GPa时可减少6.2%。在水平地震荷载作用下，增大土工格栅模量，竖向加筋效果比水平向效果更好。

图11 土工格栅模量对右坡面水平动位移峰值的影响

图12 土工格栅模量对A点竖向动位移峰值的影响

图13为不同土工格栅模量下土工格栅的拉应力峰值分布图，可以看到土工格栅模量越大，相应的土工格栅拉应力峰值也越大。桩承式加筋路堤由于桩土差异沉降，桩间土上部荷载主要由土工格栅的拉膜作用传递到桩顶。土工格栅模量越大，在相同的应变条件下，土工格栅的拉应力峰值也会越大。

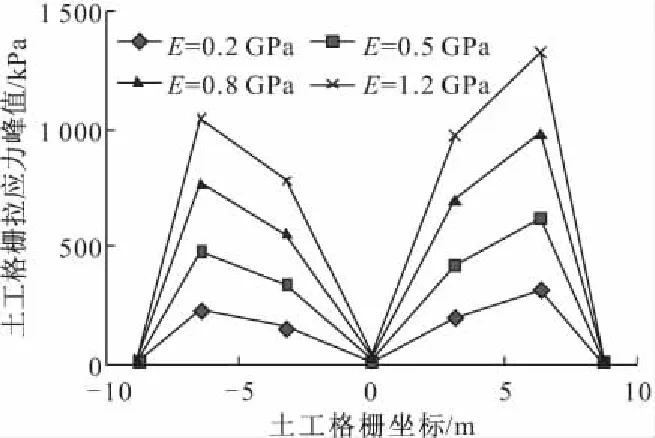
图13 土工格栅模量对格栅拉应力峰值的影响

3.2 桩间距

分别对桩间距为1.2 m、1.6 m和2.4 m的桩承式加筋路堤进行了动力分析，不同桩间距下分别对应17、13和9根桩。图14中可以看到，桩间距从2.4 m减小到1.2 m，路堤右坡面水平动位移峰值的最大值减小了2.3%。图15为不同桩间距情况下对应的A点的位移时程曲线，桩间距从1.2 m增大到1.6 m时，A点向上的位移时程曲线相位基本相同，振幅有所增加；当桩间距增大到2.4 m时，A点的位移时程曲线相位和振幅都与之前曲线有很大的差异，出现了向下振动的时间，可能是由于桩承式加筋路堤桩间距太大，在水平地震作用下土拱达到破坏。

图14 桩间距对右坡面水平动位移峰值的影响

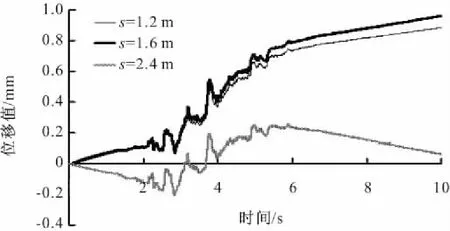
图15 桩间距对A点位移时程曲线的影响

4 结 语

本文研究了桩承式加筋路堤在水平地震波作用下的动力响应特性，并对关键参数进行了参数分析，分析了格栅模量和桩间距对桩承式加筋路堤在水平地震作用下的动力稳定性和安全性能。

(1) 桩承式加筋路堤在右坡面接近坡脚处，剪切应变增量最大，加速度峰值达到一个比较大的值，动剪应力峰值达到最大值，水平动位移峰值也达到最大值，因此综合来看，路堤填土坡脚是桩承式加筋路堤在水平地震作用下遭到破坏的地方；

(2) 在水平地震作用下，增大格栅模量能增强桩承式加筋路路堤的抗震性能，而且对增强竖向地震稳定性比水平向地震稳定性效果更明显；

(3) 可以适当增大桩间距，采用疏桩设计，使工程投资更加经济，但是增大到某个临界值后，可能导致土拱破坏。

[1] Hewlett W J, Randolph M F. Analysis of piled embankments[J]. Ground Engineering, 1988,21(3):12-18.

[2] Abusharar S W, Zheng J J, Chen B G. A simplified method for analysis of a piled embankment reinforced with geosynthetics[J]. Geotextiles and Geomembranes, 2009,27(1):39-52.

[3] 张 军,郑俊杰,马 强.路堤荷载下双向增强体复合地基受力机理分析[J].岩土工程学报,2010,32(9):1392-1398.

[4] Quang T S, Ghazi H, Patrick D B. Seismic stability analysis of piled embankments: A multiphase approach[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2010,34:91-110.

[5] 刘飞禹,余 炜,杨凤云,等.桩承式加筋路堤三维动力流固耦合分析[J].土木建筑与环境工程,2011,33(3):45-51.

[6] 刘飞禹,张 乐,余 炜,等.交通荷载作用下桩承式加筋路堤性能分析[J].土木工程学报,2011,44(s2):50-54.

[7] 李旭华.从日本地震看我国公路工程抗震设计[J].山西交通科技,2011,212(5):18-19.

[8] 黄培敏.土工格栅加筋土特性实验与抗震技术研究[D].成都:西南交通大学,2010.

[9] 王 建,姚令侃,吴 伟.路堤震害模式及路堤动力特性研究[J].岩土力学，2010，31(12)：3801-3808.

[10] 袁 捷,曾四平,祝云琪,等.地震作用下加筋土路基力学行为的弹塑性分析[J].同济大学学报(自然科学版),2008,36(4):483-487.

[11] 陈育民,仉文岗,刘汉龙.堤防地震液化数值模拟及动力反应分析[J].解放军理工大学学报(自然科学版),2011,12(3):239-224.

[12] 王 建,姚令侃,陈 强.汶川地震路堤成灾模式及土工格栅加筋变形[J].岩石力学与工程学报,2010,29(1):3387-3394.