大面积荷载下的沉降计算

介玉新，贾志杰，徐 明，陈 杰，孙 铁，李晓茹

(1.水沙科学与水利水电工程国家重点实验室(清华大学)， 北京 100084；2.招商局华建公路投资有限公司， 北京 100022； 3.建设综合勘察研究设计院有限公司， 北京 100007)

随着经济发展，采用以吹填为主的围海造陆工程来解决沿海地区“人多地少”的矛盾是必然趋势。围海造陆工程规模越来越大[1～3]。它的特点是吹填土体在水平方向的尺寸远大于竖直方向。从受力分析来看属于一种作用在地基土上的大面积荷载，荷载分布面积远大于一般建筑物基底面积。与之类似的如码头堆场、垃圾填埋场等也属于大面积荷载问题[4]。集中建设的城市建筑物在对深部土层的影响上也可以看作是大面积荷载[5～8]。本文对大面积荷载的特点进行探讨，并给出了不同情况下进行一维固结计算的差分方法。

1 大面积荷载的定义

大面积荷载目前没有严格定义，在文献[6]中作者定义大面积荷载为荷载边长(或直径)达100 m至数千米以上，远大于一般建筑物基底尺寸(<50 m)的荷载。这种定义比较直观，但不够严密。常见的大面积荷载的主要特点为：

(1)荷载分布面积很大，边长达数百米甚至数千米，远超过常规建筑物基础底面积；

(2)荷载集度q较小，一般小于50 kPa或100 kPa，小于一般建筑物的基底附加应力；

(3)变形计算深度(影响深度)不能按常规方法计算。

对于矩形荷载，当长宽比为1，z/b=0.2时荷载中心位置竖向应力系数α=0.96。也就是说，在z=0.2b深度处，可以认为分布力没有衰减(衰减量小于荷载q的5%)。所以如果荷载宽度很大，荷载的应力影响深度是很大的。但文献[1]对上海地区一6.5 km×0.5 km的堆载预压场地的观测表明，沉降影响深度约40～45 m，小于0.2b=100 m，甚至小于0.1b=50 m。即荷载的应力影响深度远大于变形影响深度(即压缩层厚度)。有理由相信在荷载大小不变的情况下，继续增加宽度b可以增大应力影响深度，但已不会增加其变形影响深度。

根据以上分析，在这里可以针对大面积荷载给出一个比较严格的定义：在荷载大小不变的情况下，继续增加荷载分布的尺寸不会改变其变形(沉降)影响深度的荷载可以称为大面积荷载。

2 大面积荷载下的沉降影响深度

在文献[6]中，作者认为变形影响深度较小的原因之一是土的模量随深度增加而增加，并采用模量随深度的计算公式Es=Es0+ξzm(其中Es为深度z处土的压缩模量，Es0为z=0处土的压缩模量，ξ、m为计算参数)来分析均质地层的沉降。

考虑到上式不易积分，这里采用如下的公式进行分析

Es=ξ(z+z0)m

(1)

上式中z0为计算参数。其它意义同上。

由于大面积荷载的附加应力在变形影响深度内几乎不衰减。所以可以认为沉降计算范围内附加应力p不变。由此引起的某一地层位置z的压缩量为p/Es·dz，积分可得从地表到深度z的压缩量，也即地表沉降量为

(2)

在m=1时，可以得到

(3a)

其他情况下，即m≠1时

(3b)

文献[6]的研究表明，经典理论框架下一般0≤m≤1，并不满足上述条件。寻找沉降影响深度的原因应当从其它方向着手。

黏性土的结构性是另一个可能原因。试验表明在附加应力小于某一门限值时天然黏性土的变形不显著，即此时土的压缩模量会比较大。但这些原因仍不足以解释沉降影响深度的有关规律。更根本的原因可能是小应变下天然土的变形模量非常大，它的影响可能超过土的结构性的影响，或者天然黏性土的结构性本身就包含了小应变的影响。

小应变问题最早发现于二十世纪七十年代，2000年前后在我国引起重视。对小应变下土的力学行为的认识有助于解释室内压缩试验得到的土的模量参数与现场反算相比总是偏小，以及大面积荷载下沉降影响深度只是有限深度等现象。但目前的研究极其有限，且主要针对较硬的土层，对软土地基小应变的研究则几乎是空白。

研究表明在非常小的应变情况下土体刚度和应变率无关、动静力刚度是基本一致的[9, 10]。文献[11]将动力方法确定的初始剪切模量G0作为静载情况下的初始剪切模量。利用泊松比确定初始变形模量，即当应变小于门限值(近似取0.001%)时

E0=2(1+μ)G0

(4)

G0可以由剪切波速确定，也可以用经验公式确定[11～13]。

Viggiani和Atkinson (1995)[14]通过弯曲单元对正常固结和超固结高岭土在微小应变(0.001%)下的剪切应变G0进行了研究，得到经验公式：

(5)

式中，pr=1 kPa，A=2088，r=0.653；R0为与固结情况有关的系数，对正常固结土，R0=1。按上述公式，可以得到地面以下50 m深度处约为G0=140 MPa，取μ=0.3，由G0可以按E0=2(1+μ)G0计算变形模量，为364 MPa，压缩模量Es=E0/[1-2μ2/(1-μ)]，为490 MPa。

当应变大于门限值时，刚度随应变增长而迅速衰减。Clayton和Heymann(2000)[15]研究了正常固结软黏土的刚度折减规律，得到E0.01/E0=0.8、E0.1/E0=0.4、E1/E0=0.1。其中E0.01、E0.1、E1分别为应变0.01%、0.1%、1%时的变形模量。可以看出，土的模量会随应变的增加而迅速降低。通常室内试验的应变都大于1%，远远大于现场土的应变，这就是室内试验得到的土的变形模量总是比实际要小的原因所在。也就是说，虽然确实存在土样扰动、应力释放、试验误差等原因，但这些原因不足于导致太大的差别。根本原因应当在于小应变与大应变模量的巨大差别上。

考虑小应变的影响，假定土的压缩模量为

Es=ξ(z+z0)mε-n

(6)

则可以得到一点的应变为

(7a)

即

(7b)

式中，α=m/(1-n)，β=(p/ξ)1/(1-n)。仿照式(3)进行积分，有

(8)

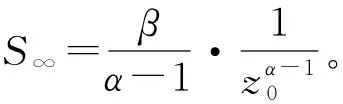
参照式(5)，m可取0.65左右。根据文献[16]，n值可以达到0.4或0.5，因此m+n>1是能够满足的。这样就解释了沉降影响深度为有限值的原因。

如果把某一深度z以内的压缩量作为总沉降量。它与S∞的误差为，

(9)

由此得到

z=(δ1-α-1)z0

(10)

给定误差δ，比如，取为5%，可以根据上式计算满足误差要求的深度z。该深度实际上也是对应该误差的沉降影响深度。可以看出，在误差δ给定的情况下，沉降影响深度与土性的关系比较密切，但与上部荷载的关系不是很大。即荷载在一定范围内波动不会改变沉降影响深度的大小。

式(6)假定压缩模量与应变为幂函数的关系。如果写不出解析关系式，可以利用曲线插值，采用数值方法计算沉降。显然，由于计算涉及的参数较难以准确获得，通过理论计算确定沉降影响深度是比较困难的。实际应用中可以通过现场实测确定某一地区的沉降影响深度。比如文献[1]采用的方法。

3 一维固结问题计算的差分方法

一维固结问题可以用太沙基一维固结理论求解。其微分方程为：

(11)

其中Cv为固结系数，

(12a)

也可以写为

Cv=kEs/γw

(12b)

式中，k为渗透系数，e1为初始孔隙比，a为压缩系数，γw为水的重度。在均质土和简单边界条件下，上述微分方程存在解析解。解析解能够满足通常情况下的固结计算问题。因为一般情况下压缩层厚度较小且土性比较单一，固结系数也可以认为是常数。但在复杂边界条件、土性分层且考虑固结系数随应力或应变发生变化的情况下，解析解就显得力不从心。变通的方法是采用二维平面应变有限元程序进行计算。因为目前的有限元程序可以进行复杂边界条件下的固结计算。更合适的方法是直接用数值方法求解该微分方程。可以采用差分方法求解。

更一般的微分方程是：

(13)

对研究区间[z0,zL]等距剖分后，所得剖分网格节点上用差分代替导数，并且取隐式差分，即

代入式(13)得：

(14)

(15)

将式(14)和式(15)相加，得到：

(16)

此即Crank-Nicolson差分格式。将上式写为

(17)

式(17)确定的是三对角方程组，解此方程组即可得解。

(18)

对一单向固结问题进行计算。其中土层厚度H=7 m，土的变形模量E=15 MPa，泊松比μ=0.35，渗透系数k=0.1 m/d。在透水的上表面瞬时施加均布荷载p=100 kPa，下表面为不透水边界。采用上述差分方法计算结果与理论解的比较见图1。可以看出差分方法可以得到较好的结果。

图1 差分方法计算结果与理论解的比较

如果外部荷载变化，式(11)变为

(19)

式中，f(t)=∂σ/∂t。对于σ不变的情况，f(t)=∂σ/∂t=0；如果σ线性变化，则f(t)=const。如果σ的变化不是线性的，则可以通过差分计算f(t)。

式(19)的差分格式为：

(20)

4 考虑蠕变的差分方法计算

对软土地基来说，蠕变的影响会比较显著。在荷载不变的情况下，蠕变引起的土的压缩也会引起孔隙水压力的增长。考虑蠕变的影响。式(11)可以修正为

(21)

其中R(t)是蠕变引起的孔隙比的变化，a为压缩系数。

蠕变常采用次固结系数Cs来计算，此时

(22)

其中τ为次固结计算的初始时间。代入式(21)可得

(23)

式中，β=2.303Cs/a。

采用前面的差分方法，式(23)的差分格式为：

(24)

利用差分方法可以方便地编写程序，计算任意条件下的一维固结问题。计算出孔压变化后，可以相应地计算土层各点的应变(等于应力变化引起的应变与蠕变之和)，进而计算地表的沉降量。如果压缩系数、次固结系数等随荷载或应变的变化而变化，可以通过对式(24)的多次迭代来求解。

5 结 论

随着大规模围海造陆、预压固结工程等的开展，大面积荷载作用下地基土的变形日益受到重视。大面积荷载的特点是荷载边长很大，远大于一般建筑物的基底尺寸。更加严格的定义应当是在荷载大小不变情况下，继续增加荷载分布的尺寸不会改变其变形(沉降)影响深度。大面积荷载下的沉降影响深度远小于变形影响深度，除了土的模量随深度增加外，土的应力应变特征在小应变下不同于常规变形下的性质也是主要原因。给定误差δ可以从理论上计算出大面积荷载下的沉降影响深度。沉降影响深度主要取决于土层的性质，与上部荷载的关系相对较小。相对于显式差分方法，隐式的Crank-Nicolson差分格式具有较好的稳定性，可以用来计算一维固结问题。对于考虑蠕变的情况也可以进行计算。

[1] 金宗川，顾国荣，韩黎明，等.大面积堆载作用下软土地基变形特性[J].岩石力学与工程学报，2005，24(6)：1056-1060.

[2] 董志良，张功新，李 燕，等. 大面积围海造陆创新技术及工程实践[J]. 水运工程，2010，446(10)：54-67.

[3] 张建新，初 超. 围海造地工程综合效益评价模型的构建与应用分析[J]. 工程管理学报，2011，25(5)：526-529.

[4] 介玉新，于立群，李广信，等. 软土地基上垃圾填埋场的固结和沉降分析[J]. 工程地质学报，2006，14(s1)：532-535.

[5] 介玉新，高 燕，李广信.城市建设对地面沉降影响的原因分析[J]. 岩土工程技术, 2007，21(2)：78-82.

[6] 介玉新，高 燕，李广信,等. 城市建设中大面积荷载作用的影响深度探讨[J]. 工业建筑. 2007，37(6):57-62.

[7] 介玉新，高 燕，李广信,等. 建筑物的集中建设与等效影响荷载[C]// 第十届全国土力学及岩土工程学术会议论文集.重庆：重庆大学出版社， 2007：206-212.

[8] 介玉新，高 燕，李广信. 建筑物间距的统计规律及对附加应力的影响[J]. 工业建筑，2010，40(s1)：62-65.

[9] Jardine R J. Some observations on the kinematic nature of soil stiffness[J]. Soils and Foundations, 1992, 32(2): 111-124.

[10] Bolton M D, Wilson J M R. An experimental and theoretical comparison between static and dynamic torsional shear tests[J]. Geotechnique, 1989, 39(4): 585-599.

[11] 王海波，徐 明，宋二祥. 基于硬化土模型的小应变本构模型研究[J]. 岩土力学，2011，32(1)：39-43.

[12] Schanz T, Veremeer P A, Bonnier P G. The Hardening Soil Model: Formulation and Verification[C]∥Beyond 2000 in Computional Geotechnics-10 Years of Plaxis. Amsterdam: Balkema, 1999:281-296.

[13] Hardin B O, Black W L. Closure to vibration modulus of normally consolidated clays[J]. Journal of the Soil Mechanics and Foundations Division, 1969, 95(6): 1531-1537.

[14] Viggiani G, Atkinson J H. Stiffness of fine-grained soil at very small strain[J]. Geotechnique, 1995,45(2): 249-265.

[15] Clayton C R I, Heymann G. Stiffness of geomaterials at very small strains[J]. Geotechnique, 2001, 51(3): 245-255

[16] Cheng C Y, Dasari G R, Chow Y K, et al. Finite element analysis of tunnel-soil-pile interaction using displacement controlled model[J]. Tunnelling and Underground Space Technology, 2007, 22(4): 450-466.