基于正态信息扩散原理的路基沉降模糊可靠度分析

徐志军，郑俊杰，边晓亚

(1. 华中科技大学 土木工程与力学学院， 湖北 武汉 430074；2. 河南工业大学 土木建筑学院， 河南 郑州 450052)

在岩土工程中，传统的“容许应力设计法”将岩土参数看作“定值”。但是由于各种不确定因素的存在，这种“定值”设计法是不科学合理的。可靠性设计充分考虑了参数的不确定性，克服了传统“容许应力设计法”的不足[1]。可靠度理论将失效函数描述结构响应的“失效状态”和“可靠状态”[2]。但在实际工程中，结构的破坏并不是“一蹴而就”的。例如，在路基工程中，路基的失效和破坏之间有个“过渡过程”，在这个“过渡过程”中，路基既不是处在“可靠状态”，也不是处在“失效状态”，而是处在“模糊状态”。模糊可靠度理论很好的解决了这一问题[3]。

岩土工程可靠性分析中需要各类岩土参数的统计信息，而作为岩土工程研究对象的岩土体，由于其形成、存在条件的复杂性，受到各类复杂因素的影响，导致其力学性质的不确定性、随机性、模糊性远远大于人造材料。这就给应用概率分布对这些不确定性进行推断带来了很多困难。而确定合适合理的岩土参数概率分布模型对岩土工程可靠性分析的准确性又有着十分重要的意义。但在实际工程中，岩土参数的概率分布问题经常是在试验数据较少的条件下进行的。常用的概率分布拟合方法是先假设参数服从某几类经典分布(如正态分布和对数正态分布等)，并利用精度较高的K-S 检验法进行拟合优度检验。

信息扩散理论在工程中的参数概率分布拟合中得到了广泛的应用[4～7]。另外，在分析模糊可靠度时，常用的隶属函数存在着不同的缺陷[8, 9]。因此，本文基于正态信息扩散理论和路基沉降的现场试验数据，对路基沉降的概率分布进行了拟合。并利用拟合精度较高的Beta函数作为路基沉降模糊事件的隶属函数，给出了路基沉降模糊可靠度的分析方法，并通过工程实例验证了本文方法的有效性。

1 模糊可靠度的分析模式

在路基沉降的可靠度研究中，传统的方法将路基沉降分为“失效”和“可靠”两个泾渭分明的状态，在这两个状态中间有个明显的分界面，称为临界面，见图1，路基沉降的极限状态方程为[2]

Z=Δ-S=0

(1)

式中，Z为极限状态方程；Δ为路基的容许沉降量；S为路基实际沉降。

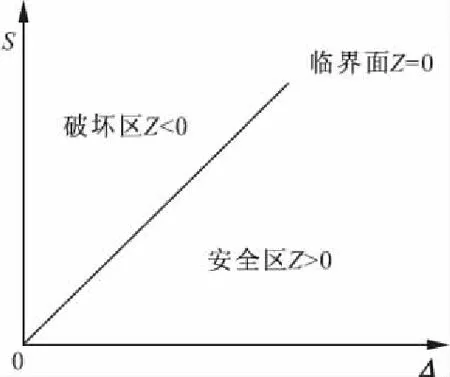
图1 极限状态

但在工程实际中，路基破坏并不是在瞬间完成的。在路基的“可靠状态”和“失效状态”之间存在一个“过渡状态”。在这个“过渡状态”中，路基既不是处在“完全可靠”状态，也不是处在“完全失效”状态，实际情况见图2，这时路基沉降的极限状态方程为[3]

(2)

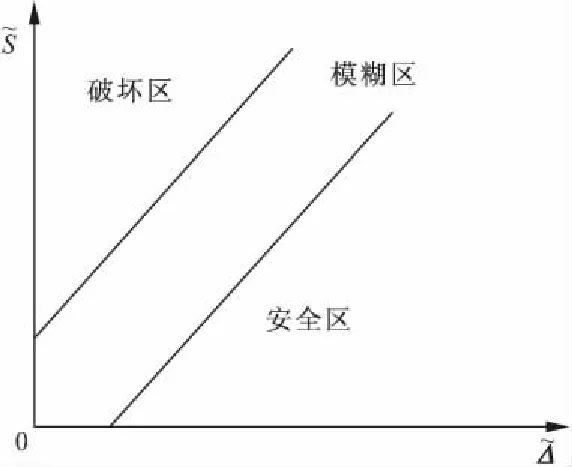
图2 模糊极限状态

传统的沉降可靠度研究虽然很好地解决了路基沉降参数的随机性，但是忽略了路基失效过程的模糊性。模糊可靠度不仅充分考虑了路基沉降失效的模糊性，同时充分考虑了随机变量的模糊性，因此研究结果更加科学合理，模糊可靠度失效概率的计算公式为[3]：

(3)

式中，fz(z)为路基沉降的概率密度函数，μA(z)为路基沉降过程的隶属函数。

2 模糊区间和隶属函数的确定

由式(1)可知，路基沉降的功能函数是

Z=Δ-S=0

在路基沉降功能函数的“0”点附近选取一个闭区间，把这个区间看作“路基可靠”到“路基失效”的过度阶段。由路基沉降的现场监测数据可计算出沉降的最大值a和最小值b。为了计算准确，选取平均加权值模糊临界区间点，即将[-(a+b)/2,(a+b)/2]确定为路基沉降的模糊临界区间。设路基的破坏过程为事件A，其隶属函数为μA(g)，μA(g)刻画了路基从完好状态到破坏状态模糊性。路基处在“完好状态”的隶属度为“1”， 路基处在“完全破坏状态”的隶属度为“0”，μA(g)为一个从“1”到“0”的连续函数。根据分布函数的特点，定义隶属函数为[9]：

(4)

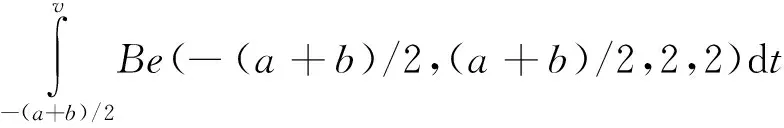
式(18)有如下的性质

(5)

这样，由Beta分布确定模糊函数不仅在整个定义域里连续光滑，而且其一次导数在整个定义域里也是连续光滑。

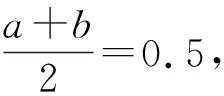
由图3可看出，μA(g)的图形“经历”了平稳过渡-缓-急-缓-平稳过渡，并且关于点(0, 0.5)为中心对称，这样既保留了传统隶属函数的优点，同时μA(g)的定义域是[0, 1]，截去传统隶属函数的“尾部”，从而克服了传统隶属函数不光滑的不足。

3 密度函数的信息扩散推断

3.1 扩散估计

设O为一随机变量，其概率密度函数为f(v)。则根据信息扩散理论，f(v)的一个总体估计为[4]：

(6)

式中，μ为定义在(-∞,+∞)的一个可测扩散函数，Δn为常数，且Δn>0，nΔn为窗宽；n为样本容量。

3.2 信息扩散原理

宫凤强等[4]给出了信息扩散原理，其定义如下：

设W=(w1,w2,…,wn)为来自母体O的知识样本；V是知识样本的基础论域。设Wi的观测值为vi；x=φ(v-vi)。则当知识样本W为非完备时，存在一函数μ(x)，使得观测值vi点获得的信息量可按μ(x)的量值扩散到v去，这时信息值为1。所得的原始信息分布能更好地反映总体的规律，可描述为：

(7)

令

φ(v-vi)=(v-vi)/Δn

(8)

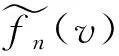
3.3 扩散函数的确定

记x点在t时刻的信息状态为μ(x,t)，由分子扩散理论可知，μ(x,t)的偏微分方程求解的表达式为：

(9)

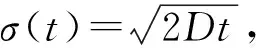
(10)

若信息扩散过程在t0时刻完成，记σ=σ(t0)，则此时所获扩散的信息可由如下函数求出。

(11)

(12)

式中，h为标准正态扩散μ(x)时的窗宽，且nh=σΔn。

设wi的观测值的最大值为vmax，最小值为vmin。利用正态信息扩散的择近原则可求解：

h=γ(vmax-vmin)/(n-1)

(13)

n取不同值时的γ值如表1所示[4]。

表1 γ的计算结果

4 实例分析

文献[11]收集了某国道上28个竣工2a后路基沉降观测点数据，见表2。由表2可知，沉降的均值和标准方差分别为15.36和8.51。取Δ=30[11]，则功能函数的均值和方差分别为14.64和8.51。因此由经典的概率理论可知，路基沉降的概率分布为[11]

p(z)=0.469e0.0069(2-14.64)2

(14)

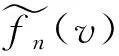
(15)

取显著性水平α=0.05，对表3中的路基沉降数据进行正态分布的假设，并用K-S法检验。K-S检验结果见表4，表4中的接受水平为检验统计量Dn和检验临界值Dn,α的比值[12]。接受水平越小即越趋近0，拟合的效果就越好。

利用表2中的监测数据作为随机变量母体的各项观测值vi见表3。

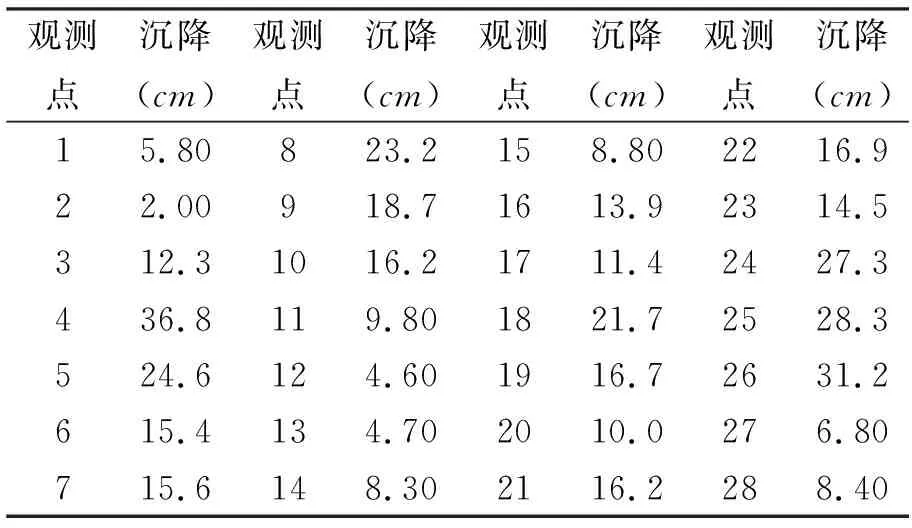
表2 路基沉降现场监测值

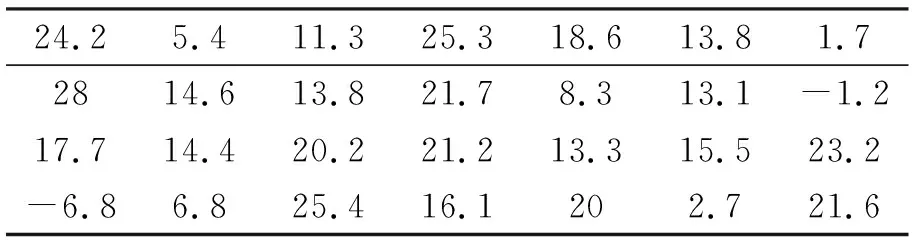
表3 母体观测值的计算结果

表4 K-S 检验法结果

由表4可知，由正态信息扩散法得到的路基沉降概率密度函数的拟合效果优于经典的概率法，能够真实反映路基沉降的概率分布情况。

由表3可知，隶属函数中的a和b值分别为-6.8和28，因此，隶属函数的表达式为：

(16)

因此，利用Matlab程序计算路基沉降的模糊失效概率为：

=0.054

(17)

算例分析表明：本文的方法不仅充分考虑了地基沉降的模糊性，而且计算精度较高，具有重要的工程意义。

[1] Phoon K K. Reliability-based Design in Geotechnical Engineering: Computations and Applications[M]. New York: Taylor & Francis, 2008.

[2] Melchers R E. Structural reliability analysis and prediction[M]. Chichester: John Wiley, 1999.

[3] 徐志军, 郑俊杰, 赵冬安. 桩式复合地基承载力的随机模糊熵可靠度分析[J]. 华中科技大学学报(自然科学版)，2010, 38(9): 104-107.

[4] 宫凤强, 李夕兵, 邓 建. 小样本岩土参数概率分布的正态信息扩散推断[J]. 岩石力学与工程学报, 2006, 25(12): 2559-2564.

[5] 周道成, 段忠东, 姚 迪, 等. 正态信息扩散法在确定河冰抗压强度概率分布中的应用[J]. 防灾减灾工程学报, 2010, 30(4): 424-430.

[6] 闫文周, 朱亮亮, 周继锋, 等. 基于熵理论的信息扩散系数确定[J]. 西安建筑科技大学学报(自然科学版), 2009, 41(2): 269-277.

[7] 张 勇, 华安增. 基于信息扩散理论的隧道系统动态稳定性分析[J]. 中国矿业大学学报, 2003, 32(3): 263-266.

[8] Zhao W Y, Xu Z J, Zheng J J. Reliability analysis of vertical bearing capacity of pile using random-fuzzy entropy principle[C]// 2010 Sixth International Conference on Natural Computation. Yantai:IEEE, 2010: 4189-4192.

[9] 郑俊杰, 刘 勇, 郭 嘉.β分布在岩土工程模糊可靠性分析中的应用[J]. 华中科技大学学报(自然科学版), 2008, 36(10): 106-109.

[10] 杨松林, 徐卫亚, 刘祖德. 岩石锚杆抗拔实验数据处理及可靠度分析[J]. 岩石力学与工程学报, 2003, 22(1): 31-34.

[11] 龚文惠, 王元汉, 郑俊杰. 基于模糊理论的膨胀土路基沉降的可靠度分析[J]. 华中科技大学学报(自然科学版), 2008, 36(2): 50-53.

[12] Ang A-H S, Tang W H. Probability concepts in engineering: emphasis on applications to civil and environmental engineering(2nd edition)[M]. New York: John Wiley & Sons, 2006.