基于剪滞理论的海底双层管线热膨胀计算方法研究

刘晓霞 贾 旭 黄 俊

（中海油研究总院）

目前我国输送高温海洋油气的管线主要是刚性连接的海底双层管线。海底双层管线内外温差较大，热膨胀可能引起管线的变形，产生内外管的轴向力，轴向力的大小是决定双层管线热屈曲的主要因素。针对海底管线的热膨胀问题，目前国内外大部分文献资料和海管设计规范都是从单层管出发，而对海底双层管线的热膨胀计算方法并没有太多的研究。Bokaian［1］从应变的角度出发利用数学分析模型研究了海底双层管线指数温度梯度、长度、重量、摩擦以及内外管相对刚度对热膨胀特性的影响规律；石云［2］从应变的角度出发得出了双层管结构的过渡段长度、管线的热膨胀位移以及内外管轴向力计算方法，但文献［1－2］都没有给出如何分析双层管线的轴向应力分布状态，而管线的轴向应力分布状态直接影响管线的屈曲行为，因此，继续开展海底双层管线的热膨胀分析研究工作具有非常重要的意义。

基于剪滞理论建立模型，提出了海底双层管线热膨胀计算的新方法。该方法可以计算得到内、外管的轴向应力分布状态和土壤摩擦力对管线轴向力的影响规律。通过实际工程中某海底双层管线热膨胀分析的实例验证，本文方法计算得到的热膨胀计算结果与工程常用方法的计算结果基本接近。本文提出的计算方法简单方便，得出的结果直观详细，该方法可以用于分析海底双层管线的热膨胀问题。

1 计算方法

双层管的受力状态比较复杂，且与多种因素有关。内管在输送介质的高温和内压作用下产生轴向膨胀，内外管之间的Bulkhead［1］将内管的膨胀力传递给外管，并协调内外管变形。由于双层管两端受到立管和登陆段管线的限制，并且外管受土壤摩擦力的约束，管线并不能自由变形［3］。

通常管线埋设段较长，从管线两端到管线中间土壤对外管的摩擦力是不断累积的，当累积到一定值时，在管线中间一段区域，外管并无轴向位移，此段称为管线的固定段，如图1所示。在固定段的两端各有一锚固点，这里的锚固点不是指人为对管线施加的固定位移约束的点，而是指管线在受到多种荷载作用下，管线上膨胀位移为零且距端部最近的点［4］。本文将含有锚固点的一端，简称为管线的A端，将管线的两端简称为B端，管线A端到B端的部分称为滑移段，在管线的两端，内管和外管由Bulkhead焊接。

图1 双层海底管线热膨胀示意图

1.1 基本假设

计算双层管线的热膨胀问题主要基于以下假设：①忽略初始热残余应力的影响；②内、外管的变形都在弹性变形范围内；③在双层管线外围有半径为R的土壤，受到外管和土壤界面剪应力的影响；④外管与土壤的最大剪切力和摩擦力相等；⑤土壤对外管的摩擦力沿外管管线均匀分布；⑥温差沿管线均匀分布；⑦忽略管线内、外压力的影响；⑧管线两端有弹簧约束。

1.2 剪滞理论模型

图2给出了剪滞理论模型示意图，在管线轴向取一微段d x，因为内管和外管在两端x＝±L处相连接，所以该小微段只考虑外管和外部半径为R的土壤。设外管在x处的应力为σf，则在x＋d x处的应力为σf＋dσf，利用剪滞理论［5－10］，得到外管轴向力平衡方程

整理得

图2 剪滞理论模型示意图

根据外管与土壤界面的剪应力是否达到最大剪应力，把整个外管分为两部分来考虑：一部分是外管与土壤界面的剪应力没有达到最大剪应力时，外管和土壤之间没有滑移，该部分为固定段，轴向应力分布由σfc表示；另一部分是外管与土壤界面的剪应力达到最大的剪应力，外管和土壤之间发生滑移，该部分为滑移段，轴向应力分布由σfb表示。以下分别对这两部分建立应力平衡方程。

1.2.1 固定段部分

在固定段，外管与土壤界面的剪切力可以根据剪切力平衡以及胡克定律得到

对上两式积分得

把式（6）代入式（2）得

对式（7）关于x求导，得

解方程（8）得到外管轴向的应力分布为

设两端滑移段的长度都为m L，外管固定段符合式（9）的应力分布，所以边界条件为

式（10）中，σfi为x＝±（1－m）L时外管的应力。

可以确定固定段的轴向应力分布为

对式（11）关于x求导得

因为外管在x＝（1－m）L处与土壤处于固定和滑移的临界状态，所以在x＝（1－m）L处土壤对外管的剪应力达到了最大值，再根据式（2）得到固定段和滑移段临界点处的轴向应力σfi为

把上式代入式（11），固定段的轴向应力可以重新写为

对式（12）求极值，可以发现最小轴向应力出现在x＝0处，即

1.2.2 滑移段部分

在滑移段，外管与土壤界面达到最大剪应力，外管和土壤之间发生滑移，外管与土壤界面的剪应力等于常量，即τ＝τs，由公式（2）以及边界条件（当x＝L时，外管的轴向应力等于σfL）可以得到滑移段的轴向应力分布

由于内外管在管线端部连接在一起，则内、外管的轴向位移相同，因此，内管的应变为uf/L，根据内管的本构关系（与外管相同），内管的轴向应力为

根据双层管线端部的轴向力平衡，建立平衡方程

将式（17）代入式（18），可以得到外管端部的轴向应力为

把式（19）代入式（16），滑移段的轴向应力可以重新写为

整个外管的轴向应力分布表达式为

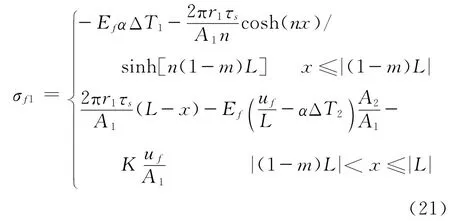
式（21）中2个未知变量uf和m 还需要确定，uf可以通过内外管的位移协调条件确定，m可以由滑移段和固定段相连接处的应力连续条件确定。

1.2.3 确定未知变量uf和m

由于内外管的位移相等，建立内外管的位移协调方程

对式（22）整理得到热膨胀位移uf的表达式

式（23）中uf也与未知变量m 相关，接下来通过应力连续条件确定变量m的值。

由应力连续条件，当x＝±（1－m）L时

由公式（16）和（14）得到滑移长度比例系数

式（25）中m的值需要利用数值迭代求解得到。

1.2.4 确定外管的应力分布

外管的平均轴向应力可以由滑移段轴向应力和固定段轴向应力平均得到

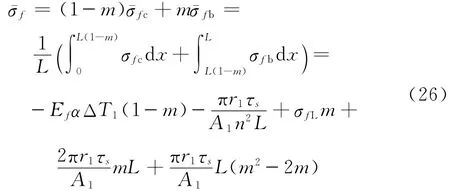
把式（11）和式（16）代入式（2）中可以得到外管与土壤界面处剪应力分布

由公式（25）得到m值的大小，如果0≤m≤1，则外管的轴向应力分布由式（21）得到，剪应力由式（27）得到。如果通过式（25）计算得到的m值不在0≤m≤1范围内时，可以分为以下2种情况：m小于0代表外管没有滑移；m大于1代表外管全部滑移。这2种情况外管的轴向应力和剪应力的计算所需的边界条件与上面的边界条件有所不同。

（1）m＜0的情况

如果利用式（25）得到的m小于零，说明外管全部固定，滑移量为零，m应该等于零。

外管的边界条件为

把式（28）代入式（9）得到外管的轴向应力分布

由于内外管轴向位移相等，则要求

把式（19）代入式（29），式（29）代入式（30）得到

把式（31）代入式（19）、式（19）代入式（29）可得外管的轴向应力分布，把式（31）代入式（17）可得内管的轴向应力分布。

把式（29）代入式（2）得到外管与土壤界面的剪应力分布

（2）m＞1的情况

如果利用式（25）得到的m大于1，说明外管全部滑移。所以外管的轴向应力分布见式（21），由内外管位移相等得到

把式（20）代入式（33）中得到轴向位移uf

把式（34）代入式（20）可得外管的轴向应力分布，把（34）代入式（18）可得内管的轴向应力分布。

2 方法验证

根据以上的剪滞理论模型，编制计算程序，对实际工程项目中某双层输油管线进行热膨胀分析计算。管线参数及管线环境参数分别如表1和表2所示。

将本文提出的剪滞理论模型计算方法和工程常用计算方法对此双层输油管线的计算结果对比情况列于表3，分析表明：本文方法计算结果稍小于工程常用方法的计算结果，但2种分析方法的计算结果基本一致。本文建立的剪滞理论模型的计算结果较为准确，可用于分析海底双层管线的热膨胀问题。

表1 实际工程项目中某管线结构参数

表3 本文方法计算结果与工程常用方法计算结果对比

3 方法应用

3.1 轴向力分布状态分析

图3是利用本文方法计算得出的某双层输油管线外管的轴向力分布图。从图3可以看到，固定段区域受到300.71 k N均匀分布的轴向压力，从管线的锚固点到管线两端，外管的轴向应力和轴向力呈线性增加，在管线的两端，外管的轴向力达到最大值728.04 k N。利用本文方法计算得到内管的轴向压力均匀分布，轴向压力的值为754.88 k N。

图3 利用本文方法计算得到的某双层输油管线外管轴向力分布

3.2 土壤摩擦力对管线轴向力的影响

图4是外管温差ΔT1＝0时，利用本文方法计算得到的双层管线端部的轴向力与土壤摩擦力的关系曲线图。

图4 利用本文方法得到的双层管线端部轴向力与土壤摩擦力的关系

从图4可看出：土壤摩擦力的大小对双层管线内、外管轴向力的影响很大，在其它环境条件不变的情况下，随着土壤摩擦力的增大，管线轴向力增加，但增加的幅度减小，当土壤摩擦力达到19 k N/m的时候，外层管线两端的轴向力接近960 k N，并保持此值不变，此值与根据相关设计指南［11］计算的轴向力最大值（959.15 k N）非常接近。

4 结论及认识

（1）本文提出的计算方法可用于分析海底双层管线的热膨胀问题。该方法不但可以计算海底双层管线的滑移段长度，热膨胀位移以及内、外管的最大轴向力，而且可以计算得到双层管线的轴向力分布状态和土壤摩擦力对管线轴向力的影响规律。

（2）内管承受均匀分布的轴向应力和轴向力，而外管除了中间部分的固定段之外，滑移段所受的轴向应力和轴向力呈线性分布，从管线的锚固点到管线两端，外管的轴向应力和轴向力逐渐增加，在管线的两端达到最大值。

（3）土壤摩擦力的大小对双层管线轴向力的影响很大，在其它环境条件不变的情况下，随着土壤摩擦力的增大，管线轴向力增加，但增加的幅度逐渐减小，当土壤摩擦力达到某一值时，管线的轴向力不再变化。

（4）本文双层管线热膨胀分析模型是在一定的假设条件下建立的，此模型可在后续工作中得到进一步的改进。

符号注释

L—管线长度，m；Em—土壤弹性模量，MPa；Gm—土壤剪切模量，MPa；Ef—管线弹性模量，MPa；α—管线热膨胀系数，℃－1；r1—外管半径，m；r2—内管半径，m；A1—外管横截面积，m2；A2—内管横截面积，m2；ΔT1—外管温差，℃；ΔT2—内管温差，℃；σf1—外管轴向应力，MPa；σf2—内管轴向应力，MPa；σfc—固定段外管的轴向应力，MPa；σfb—滑移段外管的轴向应力，MPa；σfL—管线两端处外管的应力，MPa；τ—土壤的剪切应力，MPa；τi—外管与土壤界面的剪切应力，MPa；τs—外管与土壤的最大剪切应力，MPa；τic—固定段外管与土壤的剪切应力，MPa；τib—滑移段外管与土壤的剪切应力，MPa；W（x，r）—土壤沿x轴的位移，m；uf—管线轴向热膨胀位移，m；uR—土壤在半径处的轴向位移，m；uf1—土壤或外管在半径处的轴向位移，m；m—管线滑移长度比例系数；K—弹簧刚度，N/m。

［1］ BOKAIAN A.Thermal expansion of pipe－in－pipe systems［J］.Marine Structures，2004，17：475－500.

［2］ 石云，曹静.海底双层保温管热膨胀分析［J］.中国造船，2009，59：436－441.

［3］ 于永南，帅健，吕英民.海底埋设双层管线的温度应力及变形的计算［J］.力学与实践，1996，18（5）：27－29.

［4］ 余志兵，陈海龙.海底管线在位强度分析［J］.中国造船，2007，48（增刊）：591－598.

［5］ 顾振隆.短纤维复合材料力学［M］.北京：国防工业出版社，1987.

［6］ 杜善义，王彪.复合材料细观力学［M］.北京：科学出版社，1998.

［7］ COX H L.The elasticity and strength of paper and other fibrous materials［J］.Journal of Applied Physics，1952.

［8］ HEDGEPTH J M，DYKE P V.Local stress concentrations in imperfect filamentary composite materials［J］.Journal of Composite Materials，1967，1（3）：294－309.

［9］ FUKUDA H，KAVATA K.On the strength distribution of unidirectional fiber composites［J］.Fibre Science and Technology，1997，10（1）：53－63.

［10］ CHON C T，SUN C T.Stress discontinuous along a short fiber in fiber reinforced plastics［J］.Journal of Materials Science，1980，15：931.

［11］ 《海洋石油工程设计指南》编委会.海洋石油工程海底管线设计［M］.北京：石油工业出版社，2007.