变形介质稠油油藏产能计算＊

马奎前 刘英宪 苏彦春 赵春明 周海燕

（中海石油（中国）有限公司天津分公司）

油藏生产中把压敏效应明显的油藏称为变形介质油藏［1－2］，诸多文献研究了变形介质条件下的产能分析方法［3－9］。然而，大量的实验研究表明，很大一部分高粘度稠油油藏在表现出宾汉流体渗流特征的同时，也有明显的幂律流体渗流特征，即流体呈现出广义宾汉流体渗流特征［10］；诸多文献研究了具有启动压力及幂律特征的稠油油藏产能变化特征［11－12］，但均未见考虑介质变形条件下广义宾汉流体型的稠油油藏产能公式。为此，本文在综合考虑了宾汉及幂律流体渗流特性的基础上，建立了变形介质稠油油藏产能方程，研究结果对合理开发稠油油藏具有实际意义。

1 产能公式推导

1.1 考虑介质变形的渗流方程的推导

考虑了启动压力梯度的幂律特征的广义宾汉流体的运动方程为［13－14］

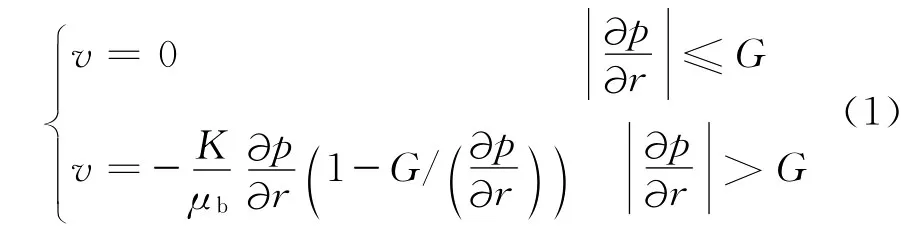
其中

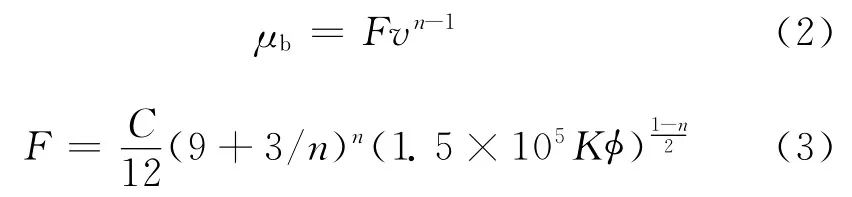
式（1）～（3）中：v为渗流速度，m/s；C 为稠度系数，Pa·sn；n为幂律指数；r为距离，m；p 为压力，MPa；μb为幂律流体的视粘度，mPa·s；G为启动压力梯度，MPa/m；φ为孔隙度，小数；K 为渗透率，μm2。

由式（1）～（3）可知，当n＝1时，μb＝F＝C，即不考虑流体幂律性时稠度系数即为牛顿流体粘度；当G＝0时，式（1）即为常规牛顿流体运动方程。

考虑变形介质中孔隙度、渗透率变化如下：

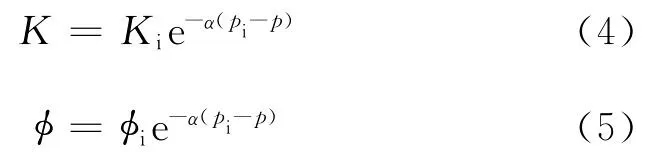
式（4）、（5）中：Ki为初始渗透率，μm2；φi为初始孔隙度，小数；α为介质变形系数，1/Pa；pi为原始地层压力，MPa。

将式（4）、（5）代入式（1），可得

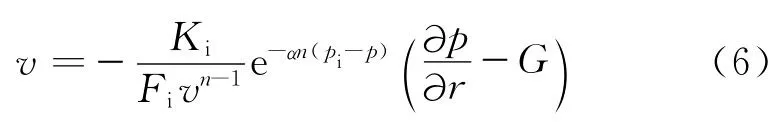
对于稳定渗流，根据达西定律可知，渗流速度表达式为

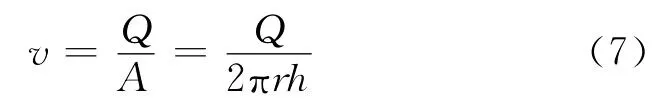
式（7）中：r为积分径向坐标，m；A 为渗流面积，m2；h为厚度，m；Q 为产量，m3/s。

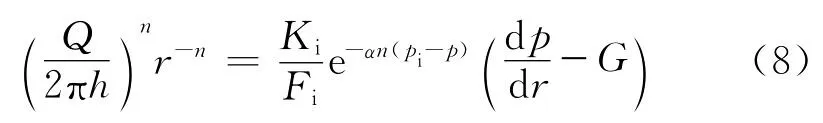
式（8）即为介质变形条件下广义宾汉流体的渗流方程。

1.2 考虑介质变形的渗流方程的求解

式（8）可简化为

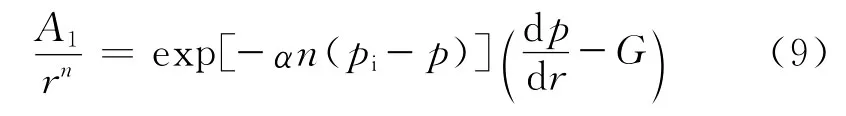
令

则式（9）变形为

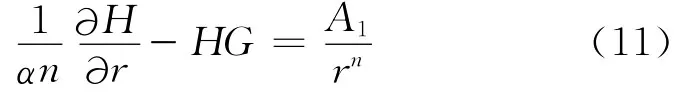
式（10）的近似解为

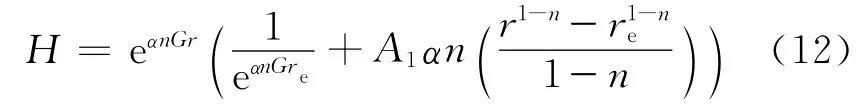
式（12）中：re为油井泄油半径，m。

将各参数代入式（12），可得

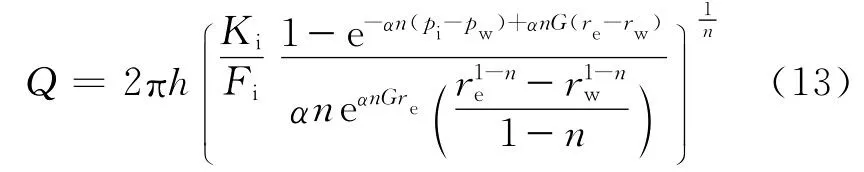
式（13）中：rw为油井半径，m。

式（13）可简化为

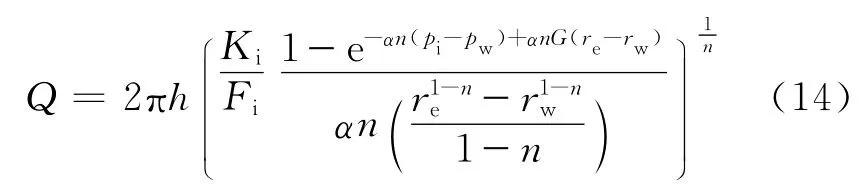
式（14）即为变形介质广义宾汉流体的产能方程。当α趋近于0时，可得

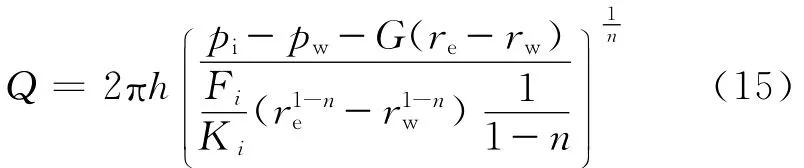
式（15）即是常规介质广义宾汉型稠油油藏产能方程。

2 产能公式验证

Y油田是具有一定天然能量的稠油油藏，具体油藏参数：原油体积系数为1.098，原始地层压力为17.8 MPa，地层渗透率为1000～2000 mD，原油粘度为151 mPa·s，井筒半径为0.1 m，幂律指数n为0.964，泄油半径为330 m，介质变形系数为0.0351/MPa，原油启动压力梯度为0.0012 MPa/m。油藏开发5年后，局部区块地层压力已降为14.1 MPa。为验证本文公式计算的准确性，将本文计算结果与文献［11］结果以及实际产能数据进行对比，结果如表1、2所示。

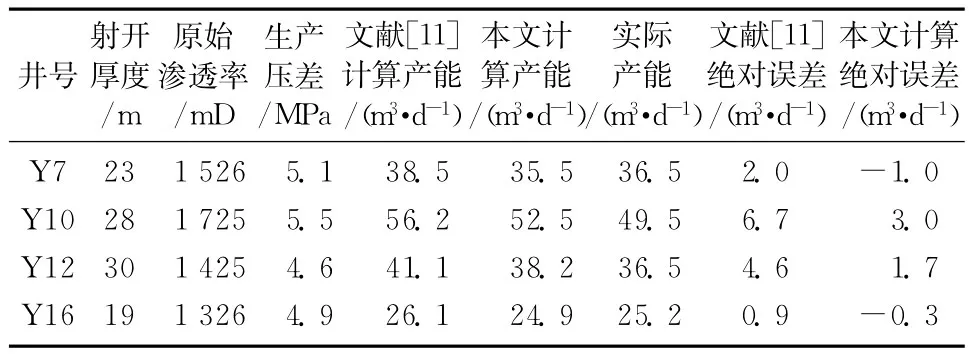
表1 本文公式计算结果与文献［11］结果及实测数据对比（投产初期）

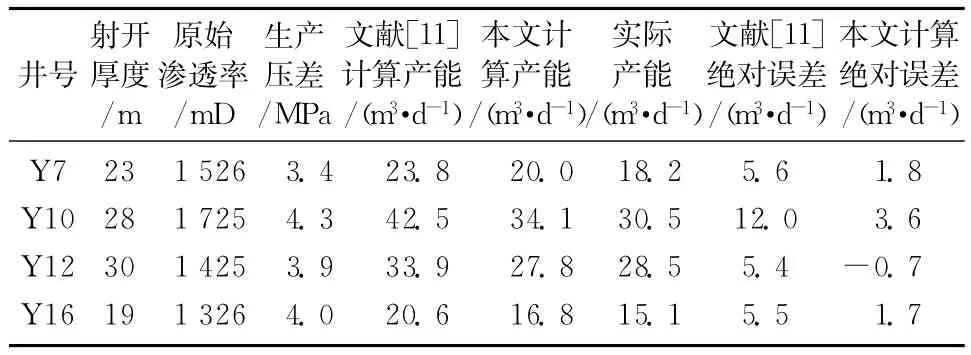
表2 本文公式计算结果与文献［11］结果及实测数据对比（地层压力降至14.1 MPa）

从表1、2的对比结果可以看出，本文公式计算误差小于利用文献［11］计算的误差，特别是当油田降压生产一定阶段后，利用本文考虑介质变形的产能公式计算的精度明显高于文献［11］得到的结果。以上对比说明，对于降压开采的变形介质稠油油藏而言，本文提供的综合考虑了幂律指数、启动压力梯度以及介质变形的产能公式计算结果更接近于实际。

3 产能影响因素分析

以Y油田Y16井地质参数为基础，讨论各参数对产能的影响程度。

通过改变启动压力梯度及幂律指数的大小，可以获得不同流体特征影响下的直井产能，计算结果如图1所示。从图1可以看出，启动压力梯度和幂律指数对产能的影响显著，随着启动压力梯度的增加，产能呈现直线下降的趋势；当幂律指数下降，即当原油非牛顿流体特征增强时，油井产能也呈现明显的下降趋势。

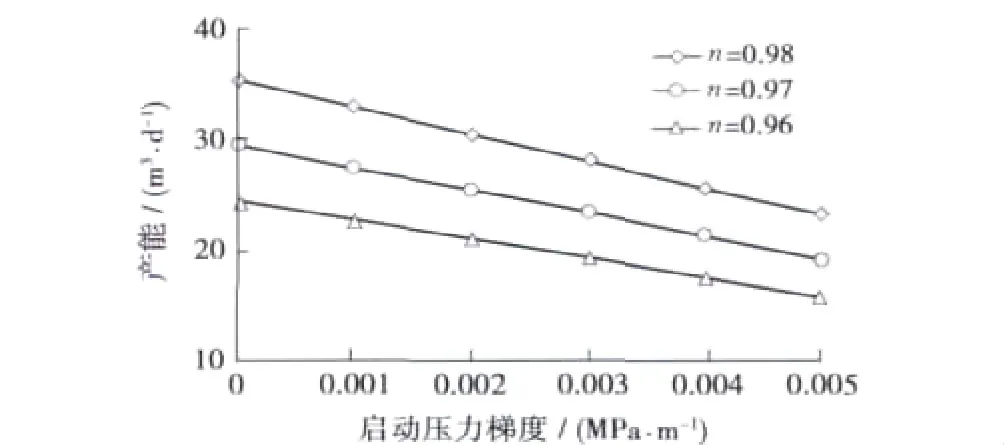
图1 Y油田Y16井不同启动压力梯度及幂律指数影响下的产能变化

图2是不同介质变形系数下油井产能与生产压差关系曲线，可以看出，当不考虑介质变形影响时，油井产能与生产压差基本呈直线关系，这符合达西定律；当考虑介质变形后，随着生产压差的增大，油井产能不再呈直线上升而是呈偏离于达西流的直线关系，而且生产压差越大，偏离达西流直线越多。这是由于生产压差的增加导致了介质变形程度愈加严重，从而造成增加相同单位的生产压差条件下，油井产能虽然上升，但是产能增加幅度却在逐渐减小，即相对于生产压差而言，考虑介质变形条件下的产能曲线呈现一种凸形曲线形态。

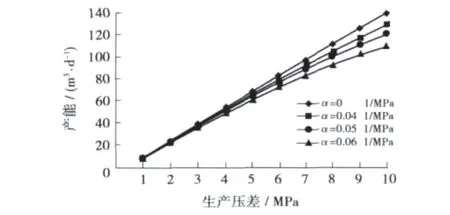
图2 Y油田Y16井不同介质变形系数下油井产能与生产压差关系曲线

由比采油指数定义式

可获得考虑介质变形条件下幂律型稠油油藏的比采油指数。由式（16）、（14）、（4）、（5）可知，当生产压差变化时，生产井附近渗透率和孔隙度的变化会引起油井比采油指数变化，这也是变形介质油藏区别于普通油藏的主要特点之一。图3是不同介质变形系数下比采油指数随生产压差变化的情况，可以看出，对于变形介质而言，存在一个最优生产压差，当超过该生产压差后，生产井比采油指数逐渐降低，而且该现象随着介质变形系数的增大而更加明显，这也是介质变形油藏的开发特征之一（对于衰竭开发的油藏而言，该现象将随着油藏压力不断下降而更为严重）。

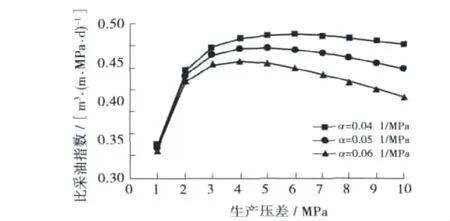
图3 Y油田Y16井不同介质变形系数下比采油指数随生产压差变化情况

4 结论

（1）本文推导的变形介质广义宾汉流体型稠油油藏的产能方程，综合考虑了介质变形、启动压力梯度、幂律指数对产能的影响；与油田实测数据对比结果表明，本文推导的方法能够更好的对油井产能进行预测。

（2）稠油油藏的原油流体性质直接影响油井产能大小，油井产能随着幂律指数的降低以及启动压力梯度的增大呈现直线下降趋势。

（3）介质变形系数越大，油井产能越低。对于变形介质油藏而言，生产井存在最优的生产压差，因此，在设计生产井工作制度时应考虑变形介质具体特点进行优化设计。

［1］ FARQUHAR R A，SMAR B G.Stress sensitivity of low permeability sandstones from the rotliegendes sandstone［C］.SPE 265011，1993.

［2］ 宋付权，刘慈群.变形介质油藏产量压力分析方法［J］.石油勘探与开发，2000，27（1）：57－59.

［3］ 苏玉亮，栾志安，张永高.变形介质油藏开发特征［J］.石油学报，2002，21（2）：51－55.

［4］ 宋付权.变形介质低渗透油藏的产能分析［J］.特种油气藏，2002，9（4）：33－35.

［5］ 陈明强，张明禄，蒲春生，等.变形介质低渗透油藏水平井产能特征［J］.石油学报，2007，28（1）：107－110.

［6］ 苗钱友，李云娟.应力敏感油藏合理工作制度的确定［J］.大庆石油学院学报，2005，29（6）：49－52.

［7］ 陈民锋，姜汉桥，郑伟，等.低渗透压敏油藏极限注采井距研究［J］.断块油气田，2010，17（5）：579－581.

［8］ 唐伏平，唐海，余贝贝，等.存在启动压力梯度时的合理注采井距确定［J］.西南石油大学学报，2007，29（4）：89－91.

［9］ 罗宪波，李波，刘英，等.存在启动压力梯度时储层动用半径的确定［J］.中国海上油气，2009，21（4）：248－249.

［10］ 张凯，李阳，王琳娜，等.稠油流变特性实验研究［J］.油气地质与采收率，2007，14（5）：91－94.

［11］ 朱维耀，鞠岩，杨正明，等.稠油油藏水平井、垂直井产能分析［J］.特种油气藏，2002，9（2）：32－33.

［12］ 刘慈群.非牛顿流体弹性径向渗流近似解［J］.力学与实践，1982，4（4）：41－43.

［13］ 刘文超，同登科，张世明.低渗透稠油油藏水平井产能计算新方法［J］.石油学报，2010，31（3）：458－462.

［14］ 孔祥言.高等渗流力学［M］.合肥：中国科学技术大学出版社，1999.