计入螺旋桨水动力的轴系校中计算

， ，

(1. 海军装备部舰船办，北京 100036；2.中国舰船研究设计中心，武汉 430064)

传统的轴系校中一般是在静态、刚性支承情况下进行，不考虑动态因素的影响。实践表明，动态因素会影响轴系校中的结果，如螺旋桨水动力产生的垂向推力、水平力矩的平均分量和交变分量。这种周期性激振力会使轴系的受力状况产生动态变化，影响轴系运行的安全性与可靠性[1-2]。

本文以某成品油船轴系为例，运用ANSYS有限元法，将螺旋桨水动力产生的周期性力和力矩等边界条件施加到轴系上，分析计算各轴承的支反力及其变化规律，并与传统轴系校中进行比较，为船舶轴系的动态校中计算提供参考。

1 轴系计算基本参数

该成品油船轴系由螺旋桨艉轴、中间轴以及主机曲轴组成，共有4个轴承支承，1#为艉轴承，2#为中间轴承，3#和4#为柴油机曲轴主轴承。从艉轴末端至曲轴前端，轴段总长为7.339 m。轴系支承位置、外部载荷见表1、2。该成品油船的螺旋桨为等螺距桨，主要参数见表3。

表1 轴系支承位置

注：与截面序号对应的轴承序号即为轴承所在处。

表2 轴系外部载荷

表3 螺旋桨参数

根据以上轴系基本参数，假定轴承为刚性支承，建立船舶轴系校中计算模型，见图1。

图1 船舶轴系校中计算模型示意

2 螺旋桨水动力平均分量与交变分量

螺旋桨水动力的平均分量是指螺旋桨在运转过程中产生的稳定的、不随时间变化的力和力矩；交变分量是指在螺旋桨运转过程中，在桨叶上产生不定常的载荷，该载荷随桨叶旋转的角度改变而发生变化[3]。在轴系校中计算时，主要考虑螺旋桨水动力产生的垂直推力Fy和水平弯矩Mz的影响。在转速一定的情况下，螺旋桨水动力的平均分量与交变分量的大小与进速系数J有关。

J=Va/nD

(1)

式中：Va——螺旋桨进速；

n——螺旋桨转速；

D——螺旋桨直径。

借助CFD软件FLUENT，建立螺旋桨水动力模型，划分桨叶网格[4]见图2。桨叶网格节点总数为14 238，面单元总数为18 636。叶面压强分布(J=0.4)见图3。

图2 螺旋桨网格划分

图3 J=0.4时叶面压强分布

通过求解叶面桨压强，得到螺旋桨水动力平均分量与交变分量。螺旋桨水动力平均分量见表4，交变分量见图4、5。

表4 螺旋桨水动力平均分量

图4 不同进速系数时交变垂直推力

图5 不同进速系数时交变水平弯矩

由表4可见，随进速系数的增大，螺旋桨垂直推力和水平弯矩均减小。当进速系数超过0.8时，推力与弯矩大大减小，说明此时推进效率会明显降低。

如图4、图5所示，螺旋桨垂直推力、水平力矩随旋转角度呈周期性变化，其周期数与叶片数相当。当进速系数J=0.4、0.7、1.0时，垂直推力的最大值分别为58.4、44.5、18.6 kN，最小值为-25.3、-15.8、-7.4 kN；水平力矩最大值分别为65.5、53.5、25.9 kN·m，最小值为-26.7、-21.9、-7.9 kN·m，这说明在一旋转周期中，垂直推力与水平力矩出现正负值。

3 轴系校中比较

进行不计入与计入螺旋桨水动力的轴系校中比较，探讨螺旋桨水动力平均分量与交变分量对轴系校中的影响水平。

3.1 不计入螺旋桨水动力的轴系校中

在不计入螺旋桨水动力的情况下，应用ANSYS有限元法，建立轴系校中有限元计算模型，求解各轴承的支反力，见表5。

3.2 计入螺旋桨水动力的轴系校中

3.2.1 平均分量对轴系校中的影响

分别将进速系数为0.4～1.1时，y方向上的垂直推力Fy和z方向上的水平弯矩Mz计入轴系校中，求得轴系各轴承支反力，见图6。

图6 轴承支反力-进速系数

由图6可见，随进速系数的增大，1#艉轴承和3#主轴承负荷增大，2#中间轴承和4#主轴承负荷减小。

与传统轴系校中相比，当J=0.4和J=1.1时，在螺旋桨垂直推力和水平弯矩平均分量的作用下，各轴承负荷见表5。

表5 计入水动力平均分量与不计入平均分量时支承反力比较 kN

由表5可见，艉轴承负荷有所减小，中间轴承负荷有一定增大，未出现“腾空”现象，受力状况得到改善；两个主机轴承上的负荷差值有所减小，但4#主机轴承负荷依然为负值，出现“腾空”现象。这说明螺旋桨水动力的平均分量能在一定程度上减小 “悬臂作用”的影响，有利于轴系校中质量的改善。

3.2.2 交变分量对轴系校中的影响

当进速系数J=0.4、0.8、1.0时，将交变垂向推力、水平力矩当作外加载荷施于轴系上，经轴系校中计算，求得各轴承负荷随叶片旋转角度的变化情况，见图7～10。

图7 交变分量对艉轴承负荷的影响

图8 交变分量对中间轴承负荷的影响

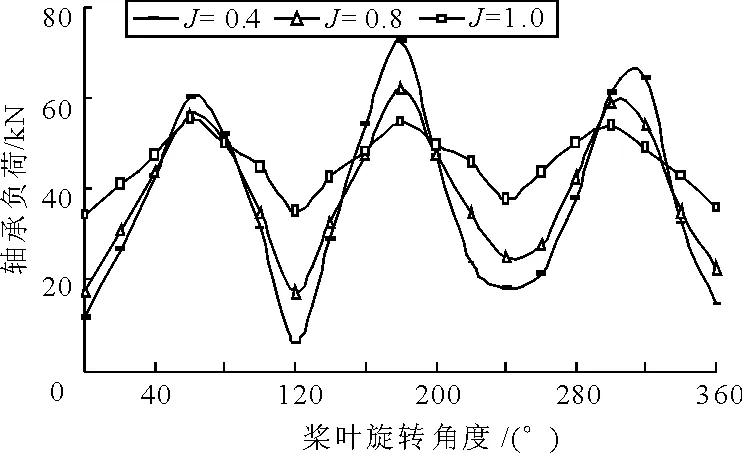
图9 交变分量对3#轴承负荷的影响

图10 交变分量对4#轴承负荷的影响

从图7～10可以得出如下结论。

1)桨叶旋转一周，轴承负荷变化周期数约为3，与桨叶数目相同。在桨叶角度为40、100、200、280、340°时，各轴承负荷分布相对合理，艉轴承负荷较小且为正值，轴系校中质量较好；在其他角度时，艉轴承负荷偏大或为负，各轴承负荷相差较大，轴系校中质量较差。

2)当进速系数J=0.4、螺旋桨桨叶转至180°时，艉轴承上的负荷最大(134.82 kN)，约为不计水动力时负荷的2倍。此时，中间轴承(-76.232 kN)出现 “腾空”。当螺旋桨桨叶转至120°时，艉轴承负荷出现最大负值(-76.232 kN)，约为不计水动力时负荷的20倍；中间轴承受力最大(94.59 kN)；主机两轴承受力较均匀。

3)当进速系数J=1.0时，艉轴承负荷波动范围在17.96～84.22 kN之间，没有负值出现，其负荷状况明显好于进速系数J=4.0时，中间轴承和3#主机轴承亦是如此；4#主机轴承负荷在桨叶旋转一个周期内呈正负交替变化，但随进速系数的增大，波动范围减小。由此可见，随进速系数的增大，一个周期内各轴承负荷的波动趋于平缓，水动力交变分量对轴系校中的影响作用减小。

4 结论

1)与传统轴系校中对比，在不同进速系数(0.4～1.1)条件下，并计入螺旋桨水动力平均分量(垂向推力和水平力矩)时，轴系的受力状况有所改善。

2)轴系校中考虑螺旋桨水动力交变分量作用时，各轴承的支反力与进速系数和螺旋桨桨叶所处角度有关。在某些角度，各轴承支反力分布比较合理，某些角度则不理想，该校中结果与传统

校中结果有所差异。

[1] 温玉奎．57300DWT散货船轴系校中研究[D].大连：大连海事大学，2007.

[2] 耿厚才．船舶轴系的动态校中计算[J]．中国造船，2006，47(3)：51-56．

[3] 何友声，王国强．螺旋桨激振力[M]．上海：上海交通大学出版社，1984．

[4] 王福军．计算流体动力学分析[M]．北京：清华大学出版社，2005．