小波变换在图像边缘检测中的应用

鲍雄伟

（长安大学 信息工程学院，陕西 西安 710064）

图像包含了人类所需要认识世界，进而改造世界的大部分的信息量。统计表明：人类所获取的信息量有是来自于图像，所以与图像相关的信息处理研究已经成为了数学、计算机科学、电子学、通信等多学科领域的跨学科研究的热门研究课题。边缘[1]包含了图像的重要信息，是指图像中灰度发生跳变的部分，是图像最基本的特征之一。因此，图像边缘检测又成为了图像处理中非常重要的研究课题之一。图像边缘检测质量的好坏，直接影响图像检索的结果。目前已经有很多的经典的边缘检测算子：Sobel算子[2]，Prewitt算子[3]，Roberts算子[4]，Log 算子[5]，Canny[6]算子等。

图像边缘就是二维图像中奇异点的集合，反映在频域内，表现为高频信号，而图像噪声也为高频信号，这使得边缘与噪声很难分得开。边缘检测不仅要从图像中检测出奇异点，还应该准确的区分出边缘与噪声。但是传统的处理算法并不能很好的区分出图像的边缘与噪声[7-8]。小波变换[9]有着非常了得的“时频”局部化分析，这为在图像的边缘检测中提供了新的方法[10]。本文充分地考虑到小波变换的特点，设计出3次样条平滑滤波算子，对图像进行了不同尺度下的小波变换，设置了合理的阈值，在每一种尺度下提取到图像的边缘，然后综合多尺度边缘形成了最后真正的边缘。

1 3次B样条小波的构造

众多参考文献[11]给出3次B样条小波在边缘提取等实际应用中渐进最优的。因此选择3次B样条小波作为平滑函数，下面来构造3次B样条小波。

Nm（x）为m次的B样条函数，由于B样条可以很好地近似Gauss函数，选择B样条的一阶微分为小波函数，m阶B样条小波就是m+1阶B样条在2j尺度上的一阶微分:

B样条函数具有偶对称性，小波函数具有奇对称性，并且小波函数与其尺度函数是正交的。考虑①当m为奇数有如下关系：

那么低通滤波器为：

那么低通滤波器为:

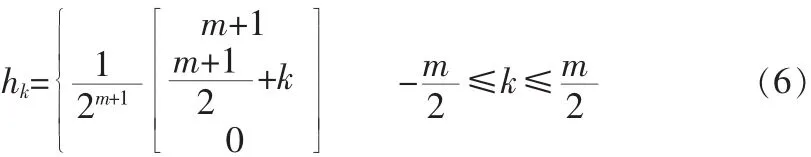
小波函数ψm与尺度函数Nm存在如下关系:

此时，有限脉冲响应不在整数节点上，调整后可得到高通滤波器的系数为：

综上，得到3次B样条滤波器的值，如表1所示。

表1 3次B样条滤波器的系数Tab.1 The filter coefficient of the third B-spline

2 小波边缘检测的构造

设二维图像信号为 I（x，y），以 θ（x，y）作为平滑函数，这样 I（x，y）经平滑之后的梯度为：

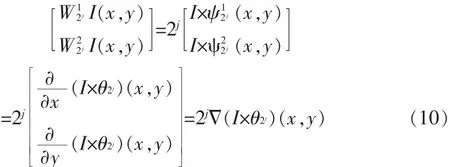
这里的尺度 S=2j，θ（x，y）沿 x，y 两个方向上的导数作为基本小波：

小波变换的两个分量在尺度为S=2j时为：

则小波变换在尺度为S=2j的模与幅角，分别为：

小波变换的模M2jI（x，y）正比于梯度向量的模，M2jI（x，y）在（x，y）方向取极大值的点对应着 I（x，y）的突变点，在尺度2j下的边缘点就是M2jI（x，y）沿梯度方向的模极大值出的点，利用该特性就可以进行图像的边缘检测。

3 利用小波变换进行图像边缘检测

多尺度局部模极大值边缘检测就是沿着梯度方向，在阈值的约束下检测出各尺度下小波变换的模极大值。在小尺度下，图像的边缘细节信息较为丰富，边缘定位精度较高，但容易受到噪声的干扰；在大尺度下，图像的边缘稳定，抗噪声性能好，但定位精度较差，所以把它们的优点集合起来，通过在不同尺度上进行综合得到最终边缘图像。即利用大尺度下能抑制噪声，可靠地识别边缘，而在小尺度下定位精度精确的优点。具体的步骤为：1）对原始图像进行预处理[1]，主要是去噪以及增强；2）对预处理后的图像进行小波变换，分别得到模图像族为 Ms（x，y）和相角图像族为 As（x，y）；3）在模图像中沿着相角方向找出模的局部极大值点，得到可能的边缘Bs（x，y），这时将其他的像素点置为零；4）将Bs（x，y）中的连续的点构成为一条链，然后求出所得到的每一条链的长度以及平均模值，设定一个合理的阈值，将那些链长和模值小于已设定的阈值的链去除掉，得到了最大尺度下单像素宽的图像 Ej（x，y）；5）对于 Ej（x，y）中的每一条链的两端点，在（j-1）尺度下搜索对应位置处的3×3邻域，将模值相近且幅角相似的点补充到边缘图像 Ej（x，y），生成 Ej-1（x，j）边缘图像；6）再次让 j减 1，依次循环，直到j=1，即为最后综合形成的边缘图像。

4 实验结果与分析

将本文所介绍的三次B样条小波变换的边缘检测与多尺度边缘综合的方法相结合，得到如图所示的结果。图1中（a）lena 原始图像；（b）prewitt算子对 lena 原始图像进行边缘检测的结果；（c）本文方法对lena原始图像进行边缘检测的结果。 图 2 中（a）lena加椒盐噪声后的图像；（b）prewitt算子对lena含噪图像进行边缘检测的结果；（c）本文方法对lena含噪图像进行边缘检测的结果。

通过Matlab仿真[12]的实验结果可以看到，利用本文所提到的方法较传统的边缘检测算子能够更加比较准确的检测到一幅图像的完整的清晰的边缘，且通过对含噪图像的检测表明传统的边缘检测方法受噪声的影响较大，抗噪声性能较差，而利用本文提出的方法则得到很好的结果。这说明本文所提到的方法不仅能准确的得到图像的完整的清晰地边缘，而且具有较强的抗噪声性能。

图1 实验结果1Fig.1 The first results of experiment

图2 实验结果2Fig.2 The second results of experiment

5 结 论

本文主要是利用B样条函数作为小波函数对图像进行小波变换，利用其多尺度特性，在不同的尺度下，对图像进行小波变换，再结合自适应阈值方法，在每种尺度下分别提取处图像的边缘，然后综合多尺度边缘，得到图像精确的单像素边缘。仿真结果表明：利用该方法得到的边缘不仅能保留丰富的细节、具有良好的抗噪型，而且边缘的定位比较准确。

[1]麦特尔（Maitre H.）．现代数字图像处理[M]．孙洪，译．北京：电子工业出版社，2006．

[2]SOBEL L.Camera Models and Machine Perception[D].Stanford:Stanford University，CA，1970.

[3]PREWITTJ.ObjectEnhancementandExtraction[M].New York:Picture Processing and Psychopictorics Press，1970:75-149.

[4]ROBERTS L G.Machine Perception of Three-Dimension Solids[C]//Optical and Electro-Optimal Information Processing.Cambridge，MA:MIT Press，1965.

[5]MARR D，HILDRETH E.Theory of Edge Detection[C]//Proceedings of the Royal Society of London，B275，1980：187-217.

[6]CANNY J.A Computational Approach to Edge Detection[J].IEEE Transaction on Pattern Analysis and Machine Intelligence，1986，8（6）:679-697.

[7]章毓晋．图像处理和分析[M]．北京：清华大学出版社，2002．

[8]曾欢，王浩．图像边缘检测算法的性能比较与分析[J]．现代电子技术，2006（14）：53-55．ZENG Huan，WANG Hao.Comparison and analysis for performance of image edge detection algorithms[J].Modern Electronic Technique，2006（14）：53-55．

[9]张贤达．现代信号处理[M]．2版．北京:清华大学出版社，1996．

[10]程正兴，林勇平．小波分析在图像科学中的应用[J].工程数学学报，2001（S1）:57-86．CHENG Zheng-xing，LIN Yong-ping.Some applications in image procession with wavelets[J].Chinese Journal of Engineering，2001（S1）:57-86．

[11]王玉平，蔡元龙.多尺度B样条小波边缘检测算子[J]．中国科学，1995（4）：426-437．WANG Yu-ping，CAI Yuan-long.Multi-scale b-spline wavelet edge detection operator[J].Science of China，1995（4）：426-437.

[12]张德丰．Matlab 小波分析[M]．北京：机械工业出版社，2009．