基于小波包-FastICA在阿尔茨海默症中的应用及其生物学分析

宫晓娜，孔 薇

（上海海事大学 信息工程学院，上海 201306）

阿尔茨海默病（Alzheimer disease，AD）是由巴伐利亚的神经病理学家阿尔茨海默[1]（Alois Alzheimer）于1907年首先发现，并以其名字而命名，这是一种渐进性的神经变性疾病，这种疾病表现为全面的认知障碍，包括：记忆、定位、判断和推理。约60%-70%老年痴呆患者为AD型[2]：AD患病率随着年龄增加而明显上升，60-64岁人群患病率为1%，而85岁以上老年人中则高达40%。AD给社会带来沉重的经济及社会负担。

近些年来随着生物芯片技术的快速发展，研究人员可以同时测定不同样本中成千上万的基因表达水平，为我们进行相关研究提供数据基础，但是每个样本都包含成千上万个基因，而我们采集的样本只有有限多个（最多几百个，对我们的研究造成很大的困难），即维数灾难（少量的样本对应着巨大数量的特征）。

针对基因表达数据的这个特点，采取了以下两种相应的解决方法[3]：

1）进行特异性基因选择，在分类的时候只使用那些与分类紧密相关的基因，这样可以筛除与分类无关的基因，减小维数、噪声和冗余，从而降低计算复杂度并提高分类的准确度和可靠度，从而减少用于实际临床的诊断费用。

2）构造分类器时采用交叉检验法。由于样本数量太少，把样本分为训练集和测试集几乎是不可能的，从而使用交叉检验法对样本进行重复利用。

1 特异性基因提取

目前，针对差异表达基因的基因排序选择算法有很多方法[4-5]，包括传统的倍数法、t检验和方差分析、Wilcoxon非参数发，Bonferroni修正法等，还有专门针对芯片数据特点的SAM[6]（significance analysis of microarray）方法等，这些方法或多或少存在某些缺陷[7]。常用的特征选取的方法包括主成分分析方法、因子分析方法、独立成分分析方法、小波变换方法和离散余弦变换方法等。相比t检验的方法，小波包变换-SAM对基因表达谱可以更有效的将不相关的冗余基因剔除。目前的聚类方法用于特征基因选取只能把一个基因归类到一类中，这不符合生物学特性，即一个基因可以参与多个信号传导过程；而ICA方法是一种双向聚类方法，能够把基因归入到不同类别中，从而较好的反应基因在不同信号传导通路中的作用[8]。本文提出的先小波包变换-SAM-FastICA算法可以充分利用每种算法的优点，克服它们的不足。实验表明这种方法比单纯的对基因表达谱数据进行ICA分析具有更高的准确度。

1.1 小波-SAM原理

由于微阵列数据自身含有很大的噪声，如何有效的消除基因表达谱数据的各种噪声，对于特异性表达基因的筛选和后续的生物学分析等有着重要的影响。

小波变换具有良好的时频局部化特性，因而能有效的从信号中提取资讯，通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析（Multiscale Analysis）。小波去噪是将信号映射到小波域，根据噪声和噪声的小波系数在不同尺度上具有不同的性质和机理，对含噪信号的小波系数进行处理。实质是减少剔除噪声产生的小波系数，最大限度的保留真实信号的系数。

由美国斯坦福大学开发的SAM软件作为插件被安装到Excel软件中使用，该软件专门用于筛选差异表达基因，其算法是基于传统的t检验和方差分析，用统计量衡量基因表达与反应变量之间关系的强弱。通过数据的重复排列或抽样来计算FDR，调节FDR筛选特异性表达基因。这种分析方法允许一定的假阳性率，适用于发现性的实验方法，有利于发现低拷贝或差异小的基因[9]。

1.2 ICA（Independent Component Analysis）算法原理

ICA算法的实质是在假设源信号统计独立的基础上，在不知道源信号及混合矩阵任何信息的情况下，试图将一组随机变量表示成统计独立的变量的线性组合。

设 X=（x1，…，xn）T为 n 维随机观测向量，由 n 个未知源信号 S=（s1，s2，…，sn）T线性组合而成。用矩阵形式来定义 ICA 线性模型

其中 si称为独立成分 （Independent Component，IC），A=（a1，a2，…，an）∈Rn×n为一满秩矩阵，称为混合矩阵。 由此可以看出，观测数据X是由独立信号源S经A线性加权得到的。进行ICA处理的目的就是找到混合信号X的一个线性变换矩阵W，使得输出尽可能的独立，即

ICA实际上是一种寻优过程，即如何使分离出的独立成分最大限度地逼近各源信号。可以通过改变P中的系数来观察Y=PS的分布如何变化。因此，ICA包括两个主要方面：目标函数和寻优算法。

1）极大化非高斯性的ICA目标函数

由ICA的估计原理2：极大非高斯性：在y的方差为常数的约束下，求线性组合非高斯的局部极大值。每个局部极大值给出一个独立成分。

在实际应用中，可以使用峭度来度量非高斯性。y的峭度kurt（y）可以定义为：

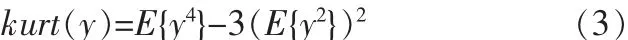
2）采用峭度的梯度算法

对混合量进行白化预处理，意味着将X线性变换成一个随机变量:

在实践中为了极大化峭度的绝对值，可以从某个向量W开始，依据可用的样本值 Z（1），…，Z（T），计算出使 Y=WTZ 的峭度绝对值增大的最快的方向，然后将向量W转到该方向。利用梯度的原理，WTZ的峭度的绝对值的梯度可以用下式计算得到：

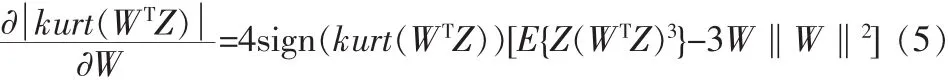
对于白化过的数据，有E{（WTZ）2}=‖W‖2。因此，可以得到下面的梯度算法：

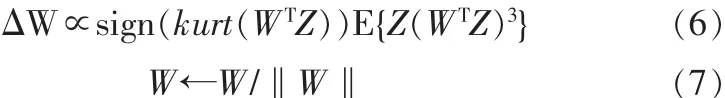
1.3 FastICA算法原理

上一节介绍了以峭度绝对值作为非高斯度量，导出了极大化非高斯的一种梯度优化方法。该梯度的算法收敛慢，且依赖于合理的学习速度序列的选择，如果学习速度选择不当，收敛性可能会被破坏。针对这个问题，1997年芬兰赫尔辛基大学的 A.Hyvärinen和 E.Oja等人提出的快速固定点算法（FastICA）[10]。

在梯度算法的一个稳定（收敛）点出，梯度必须指向W的方向，也就是说梯度必须等于一个常数标量与W的乘积。只有在这种情况下，将梯度与W相加才不改变其方向，且算法在此处收敛。令公式（5）中峭度的梯度与W相等，可以得到：

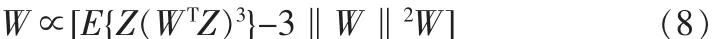
由该公式直接隐含着一个不动点算法，可以首先计算右边的项，然后将其赋给W作为新值：

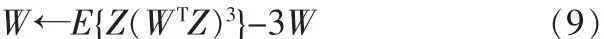
最后收敛的W以WTZ的线性组合形式可以给其中一个独立成分。

该算法能够快速且可靠地收敛。与ICA相比，该算法没有学习速度或其它可调节的参数，因此，FastICA更易用且更可靠。

1.4 小波-SAM-FastICA在基因表达谱中的应用

本次实验选用的是GEO数据库Series GSE5281中海马区（HIP）的23组AD样本数据集（13组control无病样本，10组affected AD样本，54 675个基因表达数据）。由于基因表达谱数据具有高噪声、高维性及数据分布不均衡等特点，因此，在对数据集进行FastICA特征提取之前，首先要对数据集进行预处理，即将大量的无关基因通过一定的算法筛选掉。这里采用小波包变换-SAM（Significance Analysis of Microarrays）的预处理机制，预处理后基因表达数据中的噪声大大地降低，并且能够更好地描述样本特征，有利于后期特异性基因的提取。

1.4.1 对HIP数据集预处理

首先对HIP数据集进行小波-SAM预处理，图1为不同预处理的数据聚类效果。

图1 不同预处理的数据聚类效果Fig.1 Data clustering effect of different pretreatment

（a），（b）分别为不同预处理后的数据聚类效果。从图1可以看出经过小波包-SAM筛选后的基因，经过聚类后，可以准确地将control无病样本和affected AD样本分开，证实了小波包-SAM预处理的有效性。

1.4.2 对基因表达谱提取特征基因

由于混合矩阵A可以反映特征样本在样本基因表达谱中的活跃情况，文中主要研究混合矩阵A的权重来分析基因表达谱。

图中白色和黑色分别代表正值和负值，而每个正方形的大小则对应于每个样本中成分的数量。原始数据集由13个无病样本（前 13行）和 10个AD患病 样本（最后 10行）组成。 根据正负值，从图 2（a）、2（b）中可以看出，图 2（b）第 8、9、10、11、12、13、18、21、23 列可以将无病样本和患病样本区分开，而图2（a）基本没有将无病样本和患病样本区分开。

图2 未经预处理和经小波变换的对比图Fig.2 Camparison chart of without pretrea tment and after the wavelet packet transform

根据混合矩阵A的权重图，提取FastICA分析后的相对应的第 8、9、10、11、12、13、18、21、23 个特征样本。

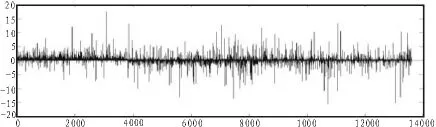
图3 Histogram of the characteristic sampleFig.3 特征样本的柱状图

由于过高表达和过低表达的基因很有可能是阿尔茨海默症致病基因或者相关基因。这里特征样本的柱状图，将基因表达值大于5或者基因表达值小于-5的基因提取出来，得到172个特征基因。

2 基于学习向量量化（LVQ）神经网络的分类

学习向量量化（LVQ）神经网络[10]是一种有监督的训练竞争层的方法。学习向量量化网络能够对任意输入向量进行分类，不管它们是不是线性可分，这点比感知器神经网络要优越得多。

实验分析：

将FastICA提取的23个样本（训练样本6个，测试样本17个）的172个基因进行LVQ神经网络分类，在MATLAB里多次运行，得到以下结果：

从表格中可以看出，经过小波包变换-SAM-FastICA提取的特征基因比小波包-SAM-ICA提取的特征基因更能高精确地将样本分类，从而验证了算法的有效性。

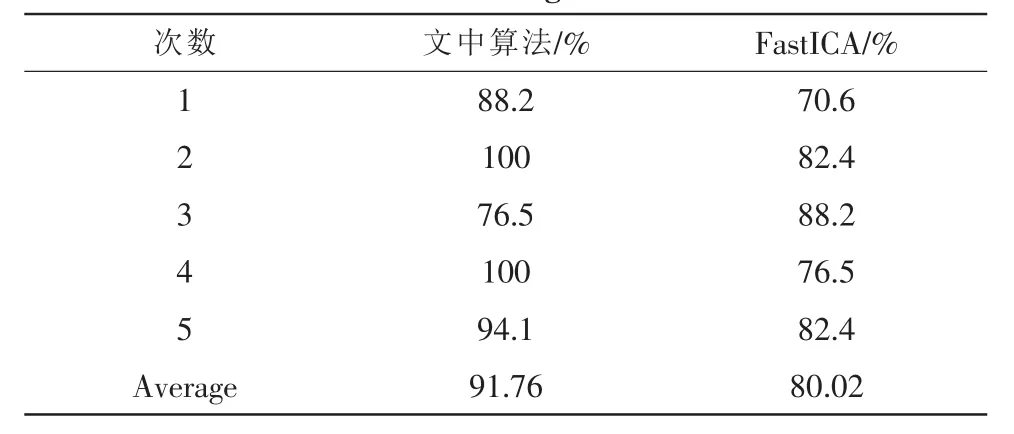
表1 对提取的基因进行LVQ神经网络分类准确率结果Tab.1 LVQ neural network classification accuracy results of the extracted gene

3 基因集合富集分析

基因功能富集分析[11]（Gene Set Enrichment Analysis，GSEA）又称功能聚类分析，利用超几何分布型统计原理来检验一组基因（共表达或差异表达）中某个功能类的显著性，通过离散分布的显著性分析、富集度分析和假阳性分析，得出与实验目的有显著关联的、低假阳性率的及靶向性的基因功能类别，该功能类别即是导致样本性状差异的最重要的功能差别，而其所属基因是需进一步验证的重要目标基因，其功能特征将阐明样本性状变化的内在生物学意义。

利用基因功能富集分析的功能特点，本文对提取的特征基因进行基因功能富集分析从而分析提取的特征基因在阿尔茨海默症数据集中的效果。

将之前进行FastICA分析筛选后的172个特征基因，经过基因富集性分析（172个基因里有139个基因匹配）分析得到它们在阿尔茨海默症数据集中的聚类情况及其它们的基因表达情况。

图4 ALZHEIMERS_DISEASE_DNBlue-Pink O'Gram in the Space of the Analyzed GeneSetFig.4 阿尔茨海默症下调基因集的蓝-粉聚集图

从图中可以发现提取的特征基因RTN3、ENC1等45个基因在阿尔茨海默症数据集的无病样本和有病样本中明显的聚类，在生物学方面验证了文中提出的算法提取特征基因的有效性。

4 结束语

通过以上实验和结果可以看出，小波包变换-SAM对基因表达谱数据具有明显的降噪作用，通过FastICA算法提取的特异性基因具有较高的分类准确性。提取的特异性基因通过基因富集性分析能够在没有先验知识的情况下也能在表达谱整体层次上对数条基因进行分析，从而从数理统计上把阿尔茨海默症的基因表达谱数据与生物学意义很好地衔接起来，这将会为疾病的诊断、治疗等方面提供重要参考。

[1]乐奕勤.阿尔茨海默氏病的发现者[J].Digest of科技文摘，2000（7）:132.LE Yi-qin.The discover of Alzheimer’s disease[J].Digest of Science and Technology，2000（7）:132.

[2]Atlas S W.Magnetic Resonance Imaging of the brain and spine[M].3rd ed.Philadelphia:Lippincott Williams and wilkins，2002.

[3]刘如云，蔡立君，易叶青.基于G-ICA的组织样本分类算法[J].计算机工程与应用，2010，46（31）:124-126，156.LIU Ru-yun，CAI Li-jun，YI Ye-qing.Classification algorithm of the tissue samples based on G-ICA [J]. Computer Engineering and Applications，2010，46（31）:124-126，156.

[4]Chen Y，Kamat V，Doughertyer R， et al.Ratio statistics of gene expression levels and applications to microarray data analysis[J].Bioinformatics，2002，18（9）:1207-1215.

[5]Krajweski P，Bocianowski J.Statistical methods for microarray assays[J].J Appl Genet，2002，43（3）:269-278.

[6]Tusher V G，Tibshirani R，Chu G，Significance analysis of microarrays applied to the ionizing radiation response[J].PNAS， 2001，98（9）:5116-5121.

[7]贺宪民，武建虎，贺佳，等.小样本情况下差异表达基因鉴别的参数统计分析[J].中国卫生统计，2005，22（3）:141-145.HE Xian-min，WU Jian-hu，HE Jia，et al.Parametric statistical analysis of differentially expressed genes identified in the case of small sample[J].China’s Health Statistics，2005，22（3）:141-145.

[8]WEI Kong.Study DNA microarray gene expression data of Alzheimer’s disease by independent component analysis[C]//International Joint Conference on Bioinformatics，Systems Biology and Intelligent Computing，Shanghai:August，2009.[9]黄得双.基因表达谱数据挖掘方法研究[M].北京：科学出版社，2009.

[10]罗亮，史晓红，徐进.LVQ神经网络方法预测蛋白质结构的二硫键[J].系统仿真学报，2007，19（9）:2077-2079.LUO Liang， SHIXiao-hong， XU Jin.Predictprotein structure of the disulfide bond based on LVQ neural network method[J].System Simulation Journal，2007，19（9）:2077-2079.

[11]Subramanian A，Tamayo P，Mootha V K.Gene set enrichiment analysis:A knowledge-based approach for interpreting genome wide expression profiles[J].PNAS，2005（102）:15545-15550.