基于ANSYS的潜油电机电磁场计算

范广玲，李春生，高云伟

（1.东北石油大学 黑龙江 大庆 163318；2.大庆油田供水公司 黑龙江 大庆 163453）

在电磁场有限元法的应用中，异步电机的电磁场计算是属于比较复杂的研究对象之一，而潜油电机因其特殊的结构和用途又是异步电机中的比较特殊的情况。国内潜油电泵技术是80年代初从美国Centlift公司和Reda公司引进的[1]。针对特殊的潜油电机的电磁场计算进行了分析和研究，对潜油电机槽型配合、槽型选择和气隙的分布提供了一些实验数据。

1 绪 论

1.1 潜油电泵系统

潜油电泵系统是一种先进的机械采油设备，多年来在大庆油田开采中发挥了重要作用。一套标准的潜油电泵系统主要由潜油电机、保护器等7个部分组成，如图1所示。

1.2 潜油电机

潜油电动机是整个潜油电泵系统中结构最复杂的一部分。目前应用的潜油电机为三相鼠笼式异步电动机。潜油电机为立式悬挂结构，主要由定子、转子、止推轴承、扶正轴承等组成，单节长度在1.5～10 m之间。大功率采用多节串联连接方式。定子的槽型有闭口槽和半闭口槽两种，潜油电机完全采用穿入式绕组结构。

图1 潜油电泵系统基本组成部分Fig.1 Electric submersible pump system major component

潜油电机特点：1）细而长的结构；2）转子分节；3）定子铁芯分节。

2 潜油电机磁场计算的数值方法

在电磁场问题中常用的数值解法有有限差分法和有限元法。任何一种适用于计算机解题的方法，都必须把连续问题（微分方程的边值问题、初值问题等）离散化，最终化成有限形式的线性代数方程组。首先对求解区域作网格剖分，用有限个网格节点代替连续区域；其次将微分算子离散化，从而把微分方程的定解问题化为线性代数方程组的求解问题。差分法和有限元法的主要区别是离散化的第二步。有限元法是从定解问题的变分形式出发，用Ritz-Galerkin方法导出相应的线性代数方程组，但基函数要按待定方式选取[2]。

2.1 有限元法

有限元法的基本问题可归纳为：

1）把问题转化成变分形式。

2）选定单元的形状，对求解域作剖分。

3）构造基函数或单元形状函数。

4）形成有限元方程（Ritz-Galerkin方程）。

5）提供有限元方程的有效解法。

2.2 区域Ω的剖分

对曲边区域Ω，一般采用三角网近似，如图2所示。三角形三边的边长一般不要相差太悬殊，但在磁场变化较小的方向上，三角形可相对地长一些。为保证计算精度，并适当节约计算的工作量，在估计磁场较强及磁场变化较大的地方，三角形要取得小一些，其他地方则可适当地取得大些。为了使三角形的三边边长不致相差过大，三角形由小到大必须逐步过渡。区域剖分后，要将所有单元和节点分别按一定的顺序编号。

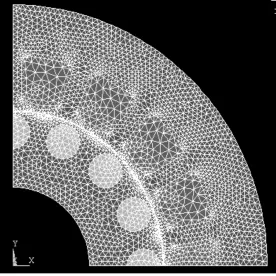
图2 网格剖分Fig.2 Split

2.3 构造基函数

在三角形元△（1，2，3）上，要构造一个次完全多项式

n=1时，p1（x，y）是一次多项式，插值节点数是3。取△（1，2，3）的3个顶点为插值节点。用待定系数法，易得

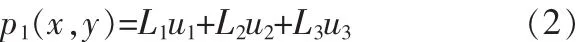
此处（L1，L2，L3）是（x，y）的面积坐标。

n=2 时，p2（x，y）是二次多项式，插值节点应取 6。 通常取△（1，2，3）的3个顶点及3边中点为插值节点。仍用待定系数法，得

其中的下标 4，5，6 依次是边 23，31，12 的中点，Lj=Li+1，Lk=Li+2，L4=L1，L5=L2，L6=L3。

还可构造3次及高次的Lagrange型公式，但最常用的是一次及二次插值公式。

从插值公式（2），（3）可直接得出基函数。

2.4 有限元方程

有2种途径形成有限元方程。假定已经按一定次序分别把节点和单元编号。第一种是工程界流行的方法，它从Ritz法及单元形状函数出发，先形成单元刚度矩阵（其阶数等于单元自由度），然后由单元刚度矩阵叠加成总刚度矩阵。第二种方法是从Galerkin法及节点基函数出发 （一个节点有几个广义坐标，就有几个基函数），直接形成有限元方程。

3 应用实例

ANSYS能模拟结构、热、流体、电、磁、声学以及多种物理场间的耦合效应。多场耦合分析使计算机虚拟样机得以实现，在产品制作之前通过仿真得到其工作性能及各种指标，实现降低研发时间，降低研发成本的目的。利用ANSYS软件的多物理场分析功能，对某典型二级三相鼠笼式潜油电机内部电磁场进行二维实体造型及电磁场分析计算[3]。

3.1 初始数据

功电流：20.374 0 A

3.2 创建物理环境

选择定子：1/4周期；

定义单位制:MKS制（m-A-s）；

单元类型及其选项:PLANE13，PLANE53

对于PLANE53单元，需要设置下列实常数：

CARE线圈横截面积 4.374 2 mm2

TURN 线圈总匝数 7

LENG方向上线圈长度 1.033 171 8 m

FILL线圈填充因子 64.884 9%

材料特性:

空气:相对磁导率为1.0 Materal1

电磁线:在已知材料库中读入Materal2

导磁材料:硅钢片（DW470-50）

手工输入B-H曲线Materal3

铜 条:在已知材料库中读入 Materal4

3.2.1 建立模型，赋予单元特性，划分网格

实体模型:

定子槽型外侧导圆:R 1.2 mm；内侧导圆:R 0.8 mm；

气隙区域:Materal1；源导体区:Materal2；

导磁区域:Materal3；绝缘区域:Materal4

网格划分：采用自由型三角形剖分，由于定子齿部和轭部磁场变化较大，因此必须对这些区域的计算网格进行加密[5]。

3.2.2 加边界条件和载荷

1）边界条件：采用周期性边界条件；

2）源电流密度；

3）在计算过程中，将转子部分设为电枢，并对电枢部分使用载荷，如图3所示[6]。

图3 电枢部分加载Fig.3 Armature part of the load

3.3 求 解

采用瞬态求解方式。

3.4 后处理

输出电磁场的磁场分布如图4所示，磁力线分布如图5所示，磁密分布如图6所示，同时计算出了定子轭部磁密和齿部磁密，如表1所示。

图4 磁场分布图Fig.4 Magnetic field distribution

图5 磁力线图Fig.5 Magnetic line of force distribution

图6 磁密分布Fig.6 Magnetic density distribution

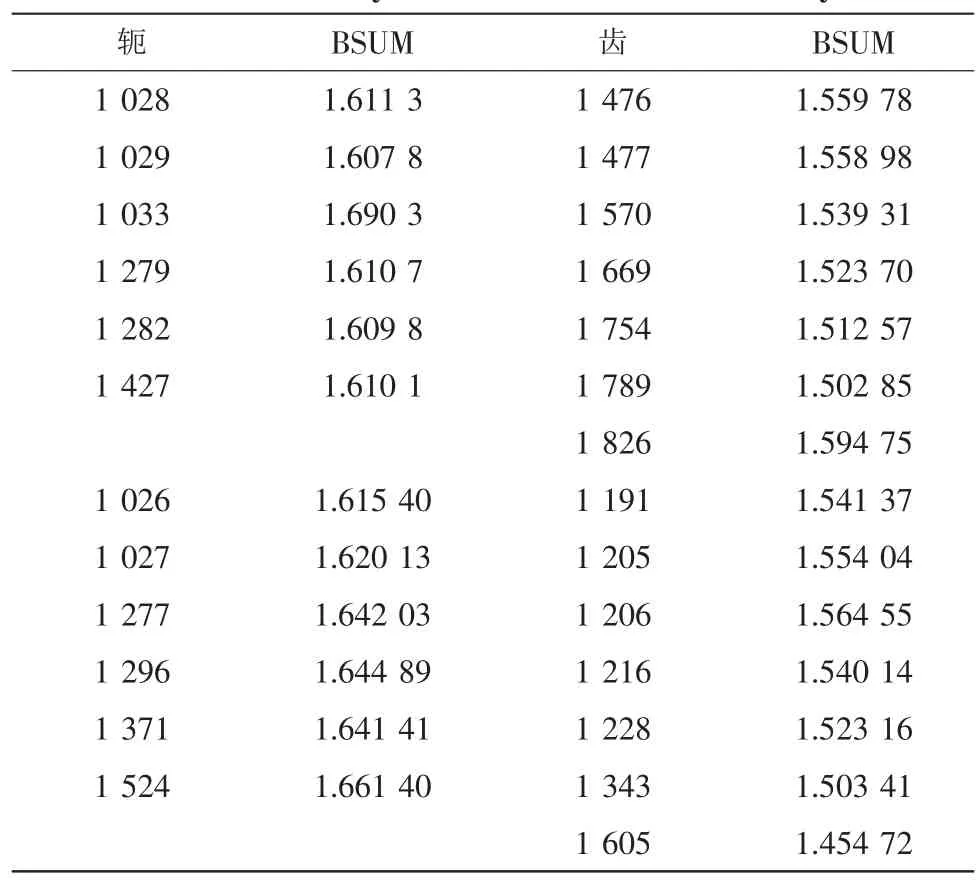
表1 定子轭部、齿部节点磁密Tab.1 Stator yoke and teeth node flux density

3.5 结果分析

从输出的结果，我们可以直观清晰地看到电机磁场和气隙的分布的情况。在磁场分布图中，在定子的中间的一相3个槽孔周围齿部和轭部磁场分布很均匀，在下一相的第一个槽孔的齿部的磁场较强。从数据可以看出在定子轭部点（节点1 033）的磁密是最强的，在定子齿部点（节点1 826）的磁密是最强的。通过这些结果可以得出的结论是该潜油电机定子采用闭口18槽，转子采用16槽的配合是比较合理的。

4 结 论

1）给出了电机电磁场分析中的有限元法的数学模型，区域的剖分，有限单元的建立。

2）给出了某潜油电机典型的电磁场的磁场分布、磁力线分布、磁密分布，同时精确地计算出了定子齿磁密、定子轭磁密、转子齿磁密、转子轭磁密的分布情况。

[1]森垂利夫特-休斯有限公司.潜油电泵手册[M].北京：石油工业出版社，1988.

[2]李荣华，冯果忱，李荣华.微分方程数值解法[M].3版.北京：高等教育出版社，1996.

[3]杨金堂，屈海端，李公法，等.基于ANSYS的U71Mn重轨轨头淬火组织场的数值模拟[J].油气田地面工程，2010，6（39）：1-4.YANG Jin-tang，QU Hai-duan，LI Gong-fa，et al.Numerical simulation of microstructure field in head of U71Mn heavy rail during quenching process based on ANSYS software[J].OIL-Gasfields Surface Engineering，2010，6（39）：1－4.

[4]王海峰，任章.ANSYS在永磁电机设计中的应用[J].中小型电机，2003，30（2）：1-3.WANG Hai-feng，REN Zhang.Application of ANSYS in design of PM motor[J].S&M Electric Machines，2003，30（2）：1-3.

[5]王国强.实用工程数值模拟技术及其在ANSYS上的实现[M].西安：西北工业大学出版社，2000.

[6]博弈创作室.APDL参数化有限元分析技术及其应用实例[M].北京：中国水利水电出版社，2004.