直扩MSK解调方法分析与仿真
付书堂 , 李 陟 , 朱学勇
(1.中国空空导弹研究院 河南 洛阳 471009;2.航空制导武器航空科技重点实验室 河南 洛阳 471009)
MSK信号是调制指数为0.5的一种连续相位调制信号(CPM),具有能量集中、包络恒定、频谱利用率高的优点,突发模式MSK信号除了具有上述优点之外,还具有持续时间短、隐蔽性好的特点,广泛应用于数据链等无线通信领域。
常用的MSK信号解调方法有两类[1-4],即“MSK逐码片检测法”和“MSK最大似然序列检测法”。MSK逐码片检测法包括包络非相干解调法、改进的差分检测法(IDD)、差分相干解调法等;最大似然序列检测法包括Viterbi判决法、最大似然分组检测法(MLBD检测法)等。
随着扩频技术的发展,MSK结合扩频的通信体制已经广泛应用于各个领域。但由于MSK信号的特殊性,使得在直扩MSK的解调方法存在局限性,相关文献也较少。上述MSK解调方法中,改进的差分检测法(IDD)、最大似然序列检测法包括Viterbi判决法、MLBD检测法等都是利用了多个码元的相关特性进行检测,这对于需要先解扩以得到处理增益的应用场合并不合适。笔者应用“MSK逐码片检测法”中的差分相干解调法和包络非相干解调法对直扩MSK信号的解调解扩实现结构进行分析与仿真。
1 直扩MSK相干解调
MSK扩频调制有多种实现方式[3],综合考虑中频数字化实现,则可采用基于正交调制的并联MSK调制方法,将MSK看作一类特殊的OQPSK,只是OQPSK两路基带信号的矩形波形被正弦脉冲所代替。MSK调制有2种形式[2],即正常形式和预编码形式。
MSK信号若直扩MSK采用相干方式解调,则调制时应当采用预编码的MSK(不带分路前的差分编码模块,如图1(a)所示),则MSK信号的数学表达式为:
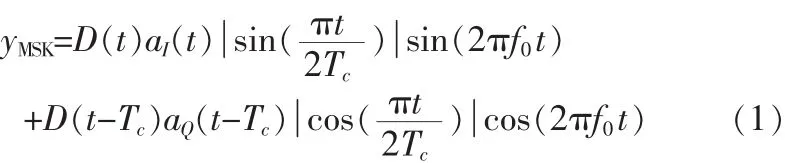
其中 D(t)表示差分编码后的信息数据,aI(t)和 aQ(t-Tc)分别为正交扩频码序列中的奇数序列和偶数序列,Tc为伪码周期。
对中频 A/D 信号分别乘以 sin(2πf0t+θ(t))和 cos(2πf0t+θ(t))(其中,θ(t)为载波相位差,它是时间 t的函数)实现数字下变频,然后经过低通滤波,得到I、Q两路信号分别为:


图1 直扩MSK相干解调方案Fig.1 Project of DSSS MSK coherent demodulation
用伪码序列ai对yI和yQ进行解扩,可以得到:

同样用伪码序列aq对yI和yQ进行解扩,可以得到:

其中 R[aQ_I(t)]与 R[aI_Q(t)]表示伪码序列的奇数序列 aI(t)与偶数序列aQ(t)的互相关函数。在伪码序列的奇数序列与偶数序列的互相关性良好的情况下,R[aQ_I(t-Tc)]≈0 和 R[aI_Q(t)]≈0,代入上式得:

将 yI_I、yQ_I和 yI_Q、yQ_Q进行组合,可以得到:
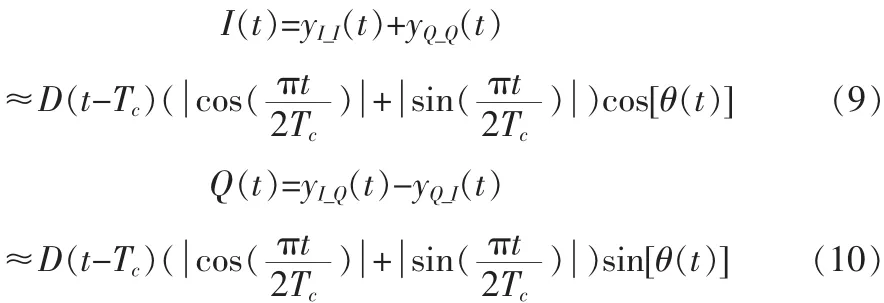
由于需要在伪随机码元周期内进行积分,故对cos((πt/2Tc) 和sin((πt)/2Tc) 在码元内积分的结果是常数,所以假设常数,D(t)在一个符号内数据相同,符号序号为k,则有

引入点积的概念,即
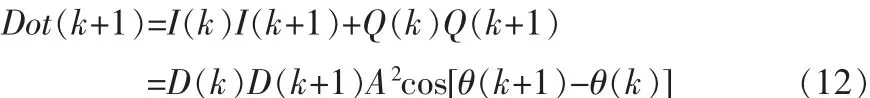
在 cos[θ(k+1)-θ(k)]>0,即信源符号间相差小于 90°时,Dot(k+1)的判决值就是差分解码后的接收数据。
2 直扩MSK信号的非相干解扩解调
若直扩MSK采用包络非相干方式解调,则调制时应当正常形式的MSK(带差分编码模块)如图2所示,则MSK信号的数学表达式为:
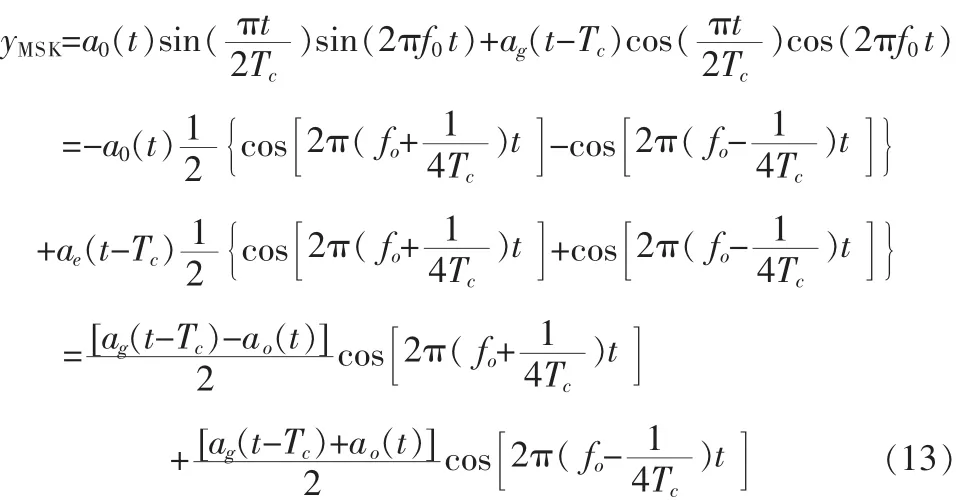
其中 a0(t)和 ae(t-Tc)分别为串并转换后的上路数据和下路数据,Tc为伪码周期。 显然的取值正好对应差分编码前的扩频数据,也即扩频后的数据0、1 正好分别对应(f0+1/4Tc)和( f0-1/4Tc)两种频率,故可以将MSK信号看成是一种2FSK信号。

图2 正常形式的直扩MSK正交调制结构Fig.2 Normal form of DS MSK orthogonal modulated structure
由于MSK信号可以看成是一种特殊的FSK信号,故直扩MSK信号也可以使用类似FSK包络非相干检测的方法进行解扩解调[5]。其中,解扩过程设置在能量计算之后,需要先进行扩频码相关运算,再将相关的结果进行判决,这样也可
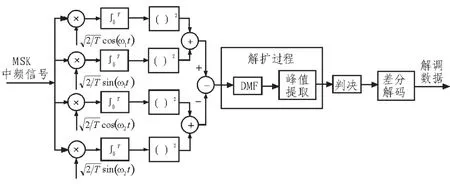
图3 直扩MSK包络非相干解调结构Fig.3 Noncoherent demodulation DS MSK envelope structure
3 性能仿真分析
在Matlab/Simulink环境下搭建直扩MSK解调相干与非相干的仿真模型,如图4所示。扩频仿真参数分别采用M序列128倍和32倍,在扩频同步良好的情况下,对AWGN信道传输性能进行的仿真结果如图5所示。
在理论上,若采用匹配滤波器在2Tc时间间隔内,独立地从预编码的MSK正交分量中恢复数据,则MSK差分相干解调应具有与BPSK相同的差错性能[1]。若在Tc时间间隔内,对正常形式的MSK信号进行FSK非相干检测,则其差错性能将比BPSK差约3.5 dB。但是由于MSK的调制指数只有0.5,不满足非相干检测正交FSK最小频率间隔1/T的要求。另外对于FSK非相干检测还有门限效应的影响,这种影响在扩频系统经常工作的负信噪比情况下愈发明显,因此在实际中,采用包络非相干检测的性能往往要差一些。
仿真结果证实了这一点,根据32位和128位M序列的仿真结果,采用非相干方式差错性能比相干方式差约4 dB和7.5 dB。但是由于实现结构简单,花费较少,且对相差、频差不敏感,故在接收信噪比要求允许的情况下,直扩MSK依然可以应用非相干方式。据文献介绍,美国Link16数据链在接收机中使用非相干方式对MSK信号进行解扩解调[6]。
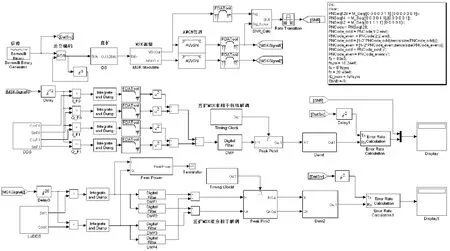
图4 直扩MSK解调仿真模型Fig.4 Demodulation simulation model of DSSS MSK

图5 AWGN信道下的性能仿真结果Fig.5 Simulation results of AWGN fading performance
4 结 论
文中利用差分相干解调法和包络非相干解调法,分别对直扩MSK信号的解调解扩实现结构进行了分析,并在Matlab/Simulink环境下建立仿真模型,对2种不同的解调方法进行仿真对比。仿真结果显示,根据32位和128位M序列,采用非相干方式差错性能比相干方式分别差约4 dB和7.5 dB。
[1]Sklar B.数字通信-基础与应用[M].2版.徐平平,译.北京:电子工业出版社,2002.
[2]Simon M K.Bandwidth-efficient digital modulation with application to deep-space communications[M].JPL Publication,2001.
[3]蔡振浩.MSK信号解调算法研究[J].通信技术,2006(S1):111-113.CAIZhen-hao.MSK signaldemodulation algorithm[J].Communications Technology,2006(S1):111-113.
[4]江志浩.MSK信号非相干检测算法研究[J].现代电子技术,2008(15):1-3.JIANG Zhi-hao.Noncoherent detection algorithm for MSK signal[J].Modern Electronic Technology,2008(15):1-3.
[5]赛景波.参数未知条件下MSK信号解调算法 [J].微型机与应用,2009(28):41-43.SAI Jing-bo.The demodulation algorithm of the MSK signal of unknown parameters[J].Microcomputeb&Its Applications,2009(28):41-43.
[6]梅文华,蔡善法.JTIDS/Link16数据链[M].北京:国防工业出版社2007.

