相控阵雷达导引头捷联去耦数字平台设计

孙彪

（贵州航天电子科技有限公司 贵州 贵阳 550009）

相控阵雷达导引头的天线阵列与弹体固连，弹体的偏航、俯仰、翻滚等剧烈的姿态运动都将直接影响到导引头对目标的截获与跟踪[1]，必须实现刚性连接条件下的捷联去耦，以隔离弹体扰动对天线波束指向的影响。随着惯性测量器件的发展，惯性器件可以不需要平台隔离，能承受较大的角速度和角加速度，同时数字计算技术的快速发展，也使得以数字方式对弹体扰动造成的天线波束指向偏差实时修正易于实现[2-5]。因此，可以采用数字捷联平台实现相控阵雷达导引头的扰动去耦，稳定天线波束在惯性空间的指向。

1 捷联去耦数字平台原理

相控阵雷达导引头数字捷联平台的基本功能是隔离弹体运动及外部扰动对天线在惯性空间指向的影响，它的基本原理是通过惯性测量单元采集弹体运动的姿态参数（偏航角、俯仰角和滚转角），根据弹体现态对运动姿态参数进行坐标变换，据此计算波束修正量，依据导引头数字信号处理机发来的波束指向码及姿态修正量，对移相器实现波束的实时控制，从而使天线无扰动地跟踪目标视线。本文设计的相控阵雷达导引头捷联去耦数字平台原理框图如图1所示。

图1 相控阵雷达导引头捷联去耦数字平台原理框图Fig.1 Strap-down decoupling digital platform of phased array radar seeker principle structure drawing

图1 中，通过弹体上的捷联惯导单元测量弹体扰动的角速度值（ωmx，ωmy，ωmz），求解弹体相对惯性坐标系的 3 个姿态角（ψ，θ，φ）并送往DSP，同时 DSP接受导引头数字信号处理机给出的当前天线波束指向的方位角和俯仰角（α，β）和目标相对天线波束中心的差角（Δα，Δβ），通过快速解算得到弹体扰动造成的天线波束指向偏差的实时方位和俯仰修正值（Δαk+1，Δβk+1），然后把计算结果及时传递给导引头的数字信号处理机，由数字信号处理机对天线波束的指向实时修正，从而实现相控阵雷达导引头的捷联去耦。

2 捷联去耦算法

2.1 坐标系定义

文中对相控阵雷达导引头捷联去耦数字平台设计过程中用到的各坐标系下坐标轴的定义如表1所示。

2.2 基于四元数法的弹体姿态角解算

弹体的扰动数据通过捷联惯性测量单元实时获取，并在惯性坐标系中求解弹体的姿态角，因此在整个导航解算过程中姿态角的求解对导航系统的制导精度具有相当大的影响。目前，捷联惯性导航系统中，姿态微分方程主要有欧拉角微分方程、四元数微分方程、方向余弦微分方程等[3]。由于采用四元数微分方程求解姿态角具有无奇异性，线性化程度高、精度高、载体可以全姿态运动等优点，因此文中采用四元数法求解弹体的姿态角。四元数法求解弹体姿态角流程图如图2所示。

表1 各坐标系中坐标轴定义说明Tab.1 Coordinate axis definition in each coordinate system

图2 四元数法求解弹体姿态角流程图Fig.2 Flow chart of missile’s attitude angle calculation based on quaternion

根据四元数理论，一个坐标系相对另一个坐标系的选择可以用四元数唯一地表示[4]。文中惯性坐标系（zg）依次绕z轴旋转 φ（滚转）、绕 y轴旋转 θ（俯仰）、绕 x轴旋转 ψ（偏航）形成弹体坐标系（zm），其坐标转换关系几何图如图3所示。

则坐标转换关系为：

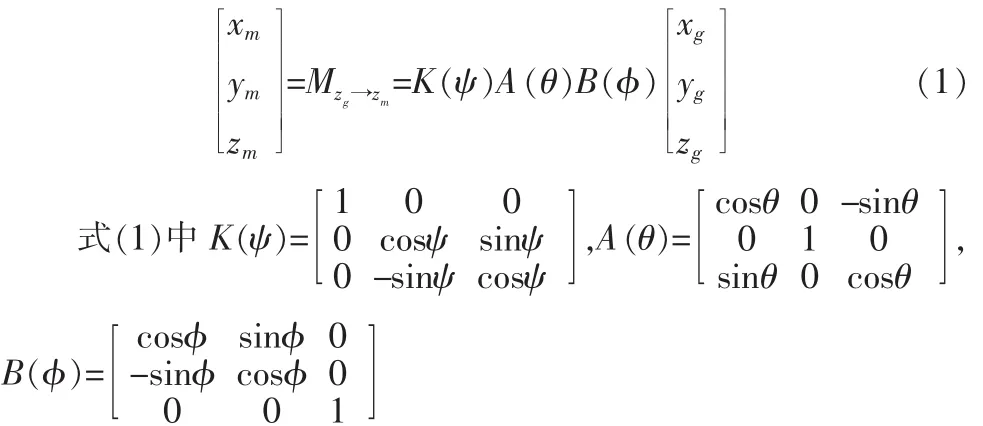
因此，弹体坐标系相对惯性坐标系的变化可以由四元数表示。 设陀螺测得的弹体角速度为 ωm（t）=[ωmx，ωmy，ωmz]T，由于惯性器件直接装在弹体上，所以陀螺测量得到的是沿弹体坐标系的绝对角速度，则弹体坐标系相对惯性坐标系的变化四元数用符号表示为：

图3 惯性坐标系向弹体坐标系转换关系几何图Fig.3 Transition geometry drawing from inertial coordinate system to missile coordinate system

由四元微分方程

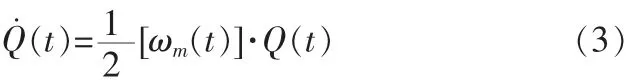
得四元数满足的矩阵方程为：

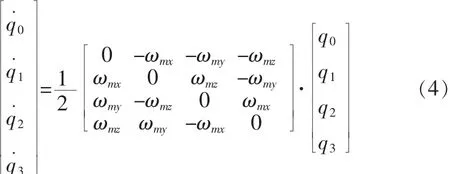
其中，四元数满足归一化条件：

我们采用四阶龙格-库塔法求解四元数微分方程。将式（4）离散化并实时地迭代求解，即可以求出 q0、q1、q2、q3的即时值。

设积分步长为T，则对式（3）有下面的迭代算法：

由上面的迭代算法可以求得四元数 q0、q1、q2、q3在每一次迭代过程中需要知道弹体运动的角速度3个点的采样值，即

惯性系到弹体系的方向余弦矩阵为：

惯性坐标系相对弹体坐标系的姿态矩阵R用四元数表示为：

式（11）和式（12）是R矩阵的两种不同表示形式，对应相等可得：

进而求得弹体姿态角为：

2.3 波束扫描稳定算法设计

相控阵雷达导引头波束扫描稳定的原理是通过对弹体姿态角的求解和目标相对天线波束中心的差角及波束中心相对弹体的夹角，经过对应坐标系的转换，解算出天线波束扫描的方位角和俯仰角，并与期望的波束指向相比较获得修正后的波束指向方位角和俯仰角，然后在波控单元中经过查找波位-波控码表获得波控码以及所有波控码的同步修正值，最后获得修正后的天线波束指向。其原理图如图4所示。

设发射瞬间，天线波束中心轴指向目标视线方向，则天线坐标系的纵轴上单位向量U0=[1，0，0]T，此时天线方位预定角为α0，俯仰预定角为β0，应用坐标变换得到发射时天线在惯性空间的瞄准线向量为：

图4 波束扫描稳定原理图Fig.4 Principle drawing of beam scanning stability

式（15）中，ψ0、θ0、φ0分别为导弹发射瞬间的偏航角、俯仰角和滚转角。

当弹体姿态变化为ψ、θ、φ时，设天线波束扫描的相应角为α、β，则此时弹体坐标系中实时跟踪线向量为：

若发射瞬间弹体坐标系与惯性坐标系保持一致，即ψ0=θ0=φ0=0，此时由式（15）和式（16）可得：

设惯性坐标系到弹体坐标系之间的变换矩阵为T，则要使天线指向稳定，必须使得

即通过不断调整天线相对弹体转角来适应弹体姿态的变化，从而保持天线在惯性坐标系中的指向不变。其中T为下面的方向余弦矩阵：

根据式（19）可得捷联稳定条件为：

展开式（21），进行进一步求解，即可得到天线实时转角为：

设弹体姿态角变化分别为：

则天线实时转角的离散公式为：

由位于机座上的惯性测量单元测得弹体角速率（ωmx，ωmy，ωmz），通过2.2节中的求解四元数微分方程实时求出弹体姿态角（ψk，θk，φk），当给定初始值（ψo，θo，φo）和（α0，β0），由 式（23）和式（24）迭代便可求出天线波束实时扫描角（αk+1，βk+1），进而得到消除弹体扰动的实时天线波束扫描修正角指令信号为：

在波束控制单元中，通过对反馈的天线波束扫描修正角指令信号进行实时处理，完成天线波束扫描角误差的补偿，使相控阵雷达导引头的天线波束稳定的指向期望方向，实现导引头的捷联去耦。

3 仿真验证

仿真1：通过在MATLAB中生成导弹惯性测量单元测量的弹体三轴角速度数据对基于四元数法求解弹体姿态角算法进行了验证。仿真条件中，弹体初始姿态角ψ=-5°，θ=30°，φ=40°，N=250。在MATLAB中生成的弹体惯性测量单元测量数据如图5所示，基于四元数法解算的弹体姿态角仿真如图6所示。

图5 弹体惯性测量单元测量数据Fig.5 Measurement data of missile’s inertial measurement unit

图6 基于四元数法解算的弹体姿态角Fig.6 Missile’s attitude angle calculation based on quaternion

通过图6可以看出，采用四元数法准确解算出了弹体的最优姿态角，同时在解算过程中不会存在奇异问题，而且计算量小，算法简单。

仿真2：将仿真1中基于四元数解算出的弹体姿态角输入到相控阵雷达导引头波束稳定单元中，对波束扫描稳定算法进行验证。仿真条件中，设弹体陀螺仪常值漂移0.01°/h，随即漂移 0.001°/h；扰动频率为 3 Hz；弹体初始姿态角 ψ=-5°，θ=30°，φ=40°；采样周期 1 ms；仿真时间 250 ms。 仿真得到的天线方位角误差如图7所示，天线俯仰角误差如图8所示。

图7 天线方位角误差Fig.7 Azimuth angle error of antenna

图8 天线俯仰角误差Fig.8 Pitching angle error of antenna

由仿真结果图7、8可知，对应给定系统，在弹体扰动频率为3 Hz情况下，等效角度扰动最大为92°，天线俯仰通的剩余角误差最大为2.4°，对给定弹体扰动频率的解耦系数达到2.6%，所以可以验证本文设计的相控阵雷达导引头捷联去耦算法正确有效。

4 结 论

相控阵雷达导引头是导引头发展的一个新领域，具有波束扫描灵活、驻留时间和空间功率可控的优点[6]，捷联去耦作为该导引头的一项关键技术，它的解决对相控阵雷达导引头的工程应用推进具有重要的作用。文中对相控阵雷达导引头中的捷联去耦数字平台进行了设计，对数字平台的捷联去耦原理、基于四元数法求解弹体姿态角、波束扫描稳定算法等内容进行了具体介绍，并对相应算法进行了原理性仿真，通过仿真结果可以看出文中设计的捷联去耦数字平台正确有效，并且具有原理简单、算法运算量小和去耦效率高的特点，对工程中解决相控阵雷达导引头的捷联去耦具有较好的指导作用。

[1]张光义.相控阵雷达系统[M].北京：国防工业出版社，1994.

[2]高烽，周辉.一种捷联式数字角信息处理系统[J].制导与引信，2000，21（4）:1-11.GAO Feng，ZHOU Hui.The digital angle data processing system of strap-down[J].Guidance&Fuze，2000，21（4）:1-11.

[3]穆虹.防空导弹雷达导引头设计 [M].北京：宇航出版社，1996.

[4]赵善友.防空导弹武器寻的制导控制系统设计 [M].北京：宇航出版社，1996.

[5]向敬明，张明友.雷达系统[M].北京：电子工业出版社，2001.

[6]曾光，卢建斌，胡卫东.多功能相控阵雷达自适应调度算法研究[J].现代雷达，2004，26（6）:14-18.ZENG Guang，LU Jian-bin，HU Wei-dong.Reaearchon adaptive scheduling algorithm for multifunction phased array radar[J].Modern Radar，2004，26（6）:14-18.