一种求解非线性约束优化问题的粒子群优化算法

罗金炎

(闽江学院数学系，福建福州 350108)

一种求解非线性约束优化问题的粒子群优化算法

罗金炎

(闽江学院数学系，福建福州 350108)

提出一种新的基于粒子群优化算法求解非线性约束优化问题的方法.通过引入自适应的退火罚因子和不可微精确罚函数来处理约束条件，可以使算法逐渐搜索到可行的极值点.数值实验证明了算法是有效的.

约束优化；模拟退火；精确罚函数法；粒子群优化算法

在实际工程和科学研究中，约束优化问题，尤其是非线性约束优化问题是一类广泛存在但又较难求解的问题，目前，此类问题的求解方法还不很成熟，仍在不断发展完善中.早期对非线性约束优化问题的求解是通过罚函数法将其转化为无约束问题来求解的，近期提出的逐次二次规划法（SQP）、逐次线性规划法（SLP）以及广义简约梯度法（GRG），已经脱离了对无约束优化方法的依赖，是目前求解非线性约束最优化问题较为有效的方法.但以上这些方法都是基于梯度寻优的方法提出的，对目标函数和约束条件有连续、可微的要求，且这些方法仅能求得局部极值点.

粒子群算法（PSO）是Kennedy和Eberhart于1995年提出的一种进化算法①Kennedy J, Eberhart R C. Particle swarm optimization [C]// Proceedings-IEEE International Conference on Neural Networks. 1995: 1942-1948.，它源于对简化社会模型的模拟，与其它进化算法相比，其思想简单，采用群体的速度——位移搜索模型容易实现，避免了复杂的进化操作.粒子群算法无需优化问题有连续性和可微性，只要求被优化的问题是可计算的，同时粒子群算法是基于群体进化的算法，且能收敛到全局最优解，因此克服了传统的基于梯度优化方法的一些缺点.目前，粒子群算法已被广泛应用于各种优化问题求解中，如调度问题、组合优化等问题.本文提出一种求解非线性约束优化问题的粒子群优化算法，并通过数值实验证明了算法的有效性.

1 基于粒子群算法的非线性约束优化方法

实际工程中的许多优化问题，最终都可化为非线性约束优化问题的求解，通常可描述为下列形式：

其中，n x∈R，f(x)是被优化的目标函数，m是等式约束个数，n是不等式约束个数.

粒子群算法与其它进化类算法相似，采用“群体”与“进化”的概念，同时依据个体（粒子）的适应值的大小进行操作，但粒子群算法不像其它进化算法那样对于个体使用进化算子，而是将每个个体看作是在搜索空间中的一个没有重量和体积的粒子，并在搜索空间中以一定的速度飞行，每个粒子的飞行速度根据其本身的飞行经验和群体的飞行经验调整.粒子群算法根据下列公式进行解的迭代更新：

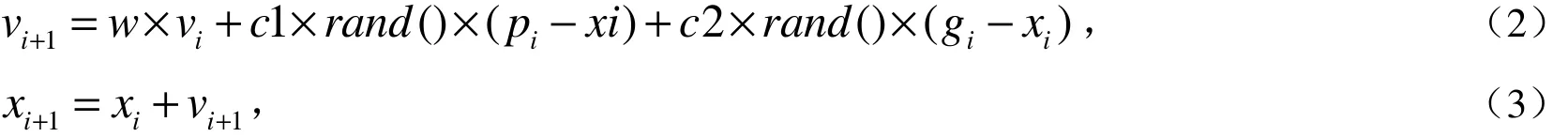
其中，w为惯性权重，rand()为均匀分布在(0,1)之间的随机数，c1和c2为学习因子.粒子的速度vi被最大速度Vmax限制，即若vi>Vmax，则令vi=Vmax，若vi<−Vmax，也令vi=Vmax.

粒子群算法求解约束优化问题的难点是约束条件的处理.文献[1]采用分离目标函数与约束条件的方法，将约束条件转化为调节函数和目标函数一起作为粒子的适应函数，每个粒子的优劣由这两个函数值按一定比较准则共同决定，但其中比较准则的确定有一定的难度.Parsopoulos等人在文献[2]中将约束优化问题转化为minmax问题，并采用粒子群算法进行求解，取得了满意的结果，但存在系数的选择问题.文献[3]引入半可行域的概念，提出了竞争选择的新规则，并对适应度函数进行改进，结合粒子群算法本身的特点，设计了选择算子，从而得到一个求解约束优化问题的新的进化算法.文献[4]将原约束函数作为以欧拉数为底的指数函数的指数变量重新构造一个辅助函数作为约束函数，采取约束函数的满足优先于目标函数的寻优，该方法虽然对约束优化问题的约束条件满足取得一定效果，但目标函数的优化效果并不明显.以上方法或多或少都与所要解决的问题有关，罚函数法则可以克服这种缺陷，它通过对不可行解施加某种惩罚，经过不断迭代后，使解群逐渐收敛于可行的极值点.采用一般的罚函数法[5]或动态罚函数法[6]来处理约束问题，计算过程需要求解一系列无约束极小问题，工作量较大，并且罚因子的选取也有一定难度，取得很大时可能陷入病态，取得过小又可能使算法的收敛性能很差.本文采用不可微精确罚函数法，不需要求解一系列无约束极小问题，采用自适应的退火罚因子可以防止罚因子取得过大或过小.通过调整自适应的退火罚因子，结合不可微精确罚函数来处理约束条件，最终可使算法逐渐收敛于有可行域的极值点，从而实现非线性约束优化问题的求解.

2 基于粒子群算法的退火罚函数优化算法

2.1 惩罚函数法

惩罚函数法最早是在最优化问题中用来处理非线性约束优化的一种方法，它通过对约束条件施加惩罚函数而使有约束问题变为无约束优化问题，从而利用成熟的无约束优化方法求解.对于式（1）的求解可以化为下列无约束问题的求解：

其中，P(σk,x)是惩罚函数，σk是惩罚因子.针对不同的惩罚函数，形成了不同的方法，主要有外罚函数法、内罚函数法、乘子法和精确罚函数法.外罚函数法和内罚函数法容易引起求解问题的病态问题，这是由它们需要罚因子无限增大而引起的.乘子法通过在罚函数中引入拉格朗日乘子λ，使得罚因子kσ可取某个有限值，因而解决了早期外罚函数和内罚函数法中出现的病态问题，但它需要解决一系列无约束极小值问题来逼近最优乘子和最优解.精确罚函数法有不可微精确罚函数和可微精确罚函数两种形式.不可微精确罚函数法的主要缺点是它在约束边界不可微，因此不能采用无约束优化中有效的梯度法.可微精确罚函数法虽可以利用梯度型算法来求解，但要利用这些函数的二阶导数，从而大大增加了无约束极小化过程的工作量.

2.2 基于粒子群算法的退火精确罚函数法

用粒子群优化算法求解约束优化问题，基本上采用罚函数的二次型形式，即：

但是，这种处理方法在某些非线性优化问题中的求解性能并不好.

为了改变上述方法的缺陷，本文采用一种模拟退火不可微精确罚函数法[7]，即罚函数的选取为如下形式：

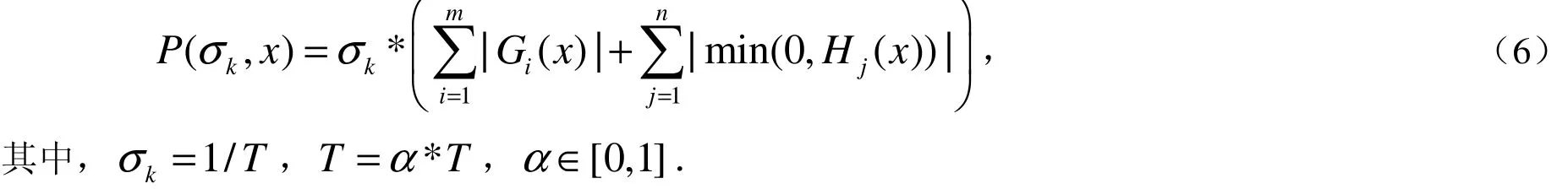
罚因子kσ吸取了模拟退火的思想，使T逐渐下降，即kσ逐渐增大，其增加速度由温度冷却参数α来控制.随着进化的不断进行，kσ逐渐增大，使得解群趋于可行解.罚函数的形式采用了不可微精确罚函数.由于粒子群算法对问题的可微性没有限制，因此克服了基于梯度型算法不能处理不可微函数的缺陷，从而能够有效地求得可行的极值点.

3 算 例

选取如下测试函数测试本文提出的算法，根据它们的目标函数值和满足的约束条件来进行综合评价.

算法的参数：惯性权重ω从0.9线性递减到0.4，学习因子参数为C1 =C2 = 1.48，温度冷却参数为α= 0.928.

算例1 测试函数为：

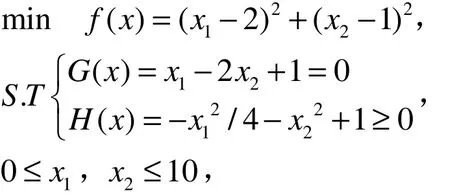
群体规模为100，个体最大速率vmax= 9.12，对该问题进行10次独立实验取平均值，并同其它算法的结果进行比较.求解结果如表1所示.由表1可知，用本文提出的方法（退火精确罚函数法）求解的结果，无论是所求得的目标函数值还是最终所满足的约束精度效果都是比较好的，虽然所求的目标函数值不如退火二次型罚函数法，但是它满足的约束精度比退火二次型罚函数法要好得多，在许多实际的优化问题中，对可行解的要求（即对约束的满足）是极为关键的.

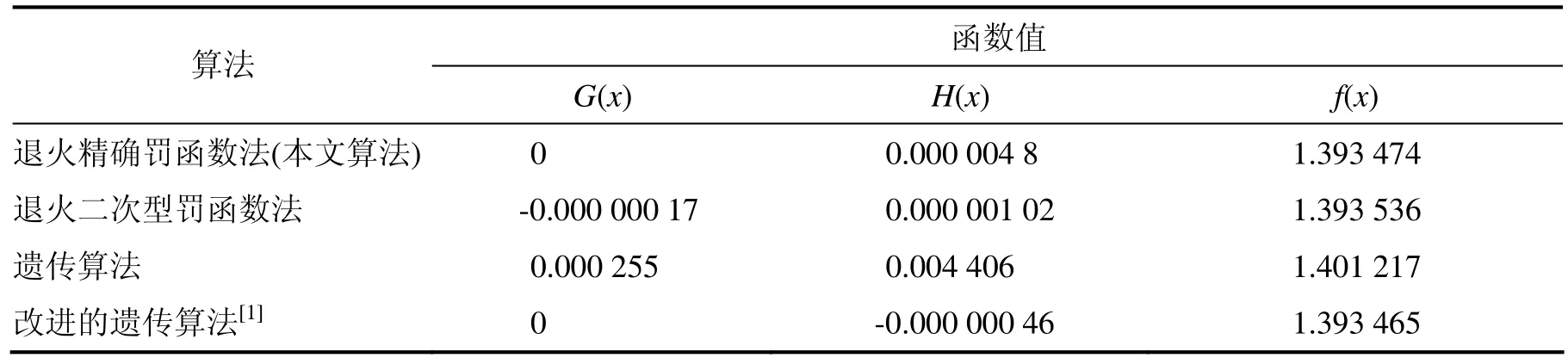
表1 算例1的数值结果比较

算例2 测试函数为：

群体规模为100，个体最大速率vmax= 16.0，求解结果如表2所示.由表2可知，本文算法在约束条件的满足和目标的寻优方面，比一般的粒子群算法的效率都好，在目标的寻优上比文献[6]中改进的粒子群算法的效率要好.

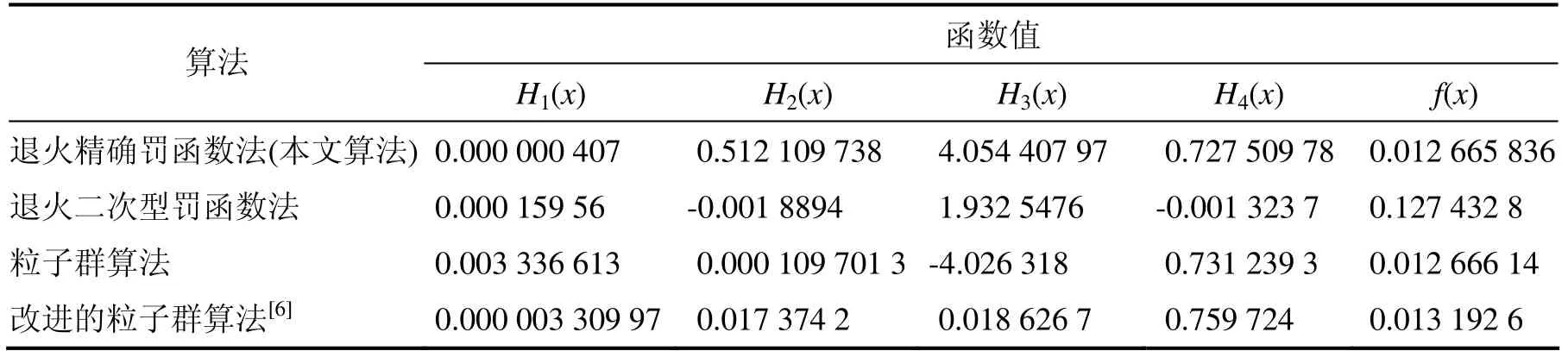
表2 算例2的数值结果比较

4 结 论

粒子群算法不要求所求解问题的连续可微性，因此可以利用基于梯度法不能求解的不可微精确罚函数法来解决非线性约束优化问题.仿真结果表明，该算法对约束条件的满足和目标寻优的效果都是比较好的.

[1]刘华蓥, 林玉娥, 王淑云, 等. 粒子群算法的改进及其在求解约束优化问题中的应用[J]. 吉林大学学报: 理学版, 2005, 43(4): 472-476.

[2]Parsopoulos K E, Vrahatis M N. Recent Approaches to Global Optimization Problems through Particle Swarm Optimization [J]. Natural Computing, 2002, (1): 235-306.

[3]张利彪, 周春光, 刘小华, 等. 求解约束优化问题的一种新的进化算法[J]. 吉林大学学报: 理学版, 2004, 42(4): 534-560.

[4]Vaz A I F. Optimization of Nonlinear Constrained Particle Swarm [J]. Technological and Economic Development of Economy, 2006, 12(1): 30-36.

[5]张喆, 李燕. 混合微粒群算法在非线性约束优化中的应用[J]. 计算机应用与软件, 2004, 21(8): 114-118.

[6]张宝菊, 单国全, 齐名军, 等. 求解非线性约束优化问题改进的粒子群算法[J]. 天津师范大学学报: 自然科学版, 2006, 26(2): 73-76.

Particle Swarm Optimization to Nonlinear Constrained Optimization Problem

LUO Jinyan
(Department of Mathematics, Minjiang University, Fuzhou, China 350108)

A new optimal method based on particle swarm optimization (PSO) to nonlinear constrained optimization problem was presented in this paper. By adopting adaptive annealing penalty factors and non-differentiable accuracy penalty function to deal with the constraints, the method could help the PSO to gradually achieve optimal extreme point. Numerical experiments demonstrated the effectiveness of the PSO.

Constrained Optimization; Simulated Annealing; Accuracy Penalty Function; Particle Swarm Optimization

(编辑：王一芳)

O224

A

1674-3563(2012)01-0001-05

10.3875/j.issn.1674-3563.2012.01.001 本文的PDF文件可以从xuebao.wzu.edu.cn获得

2011-05-18

福建省自然科学基金项目(2009J05011)；闽江学院科技启动项目(YKQ09001)

罗金炎(1975- )，男，福建上杭人，副教授，硕士，研究方向：计算数学，智能优化算法